
- •Методы построения ЭС и классификация ЭС по методам построения
- •Оценка погрешности для полинома Лагранжа
- •Разделенные разности
- •Численное интегрирование
- •В задаче линейного программирования (ЛП) целевая функция может быть представлена как сумма произведений переменных на некие константы:
- •Требования к стандартному виду задачи ЛП:
- •Разбиения
- •Классификация языков
31. Биологический подход к решению задач искусственного интеллекта. Генетические алгоритмы и их использование. Нейронные сети и их использование.
Биологический подход:
Развитие системы искуственного интеллекта (ИИ) сразу разделилось на 2 направления: биологическое и информационное.
Биологич-ое: Так как мы моделируем биологич-е системы, то необх-мо иммитировать или копировать построение реальных биологич-х систем. В данном направлении развиты:
1) бионика (разработка роботов по аналогии с биологичми существами);
2)генетич-е алгоритмы (основаны на системах естесственного отбора, системах адаптации в биологии);
3)нейронные сети (моделируются нейроны); 4)моделир-ние конкуренции, мотивации; агентные
системы (моделир-е жизни, развития, адаптации); 5)нейрокибернетика (теория управления, основанная на
нейронных сетях). Генетические алгоритмы (ГА):
В природе мощный механизм естественного отбора, который в рамках 1 популяции проходит следующие этапы:
1)начальная популяция – набор исходных биолог-х существ;
2)искусственный отбор – в результате воздействия окруж-й среды и конкуренции из популяции отбир-ся лучшие эл-ты;
3)появл-е (рожд-е) нового поколения с использ-ем 2-х мехмов – мутации в генах и скрещивания между генами родителей.
Мутация – это случ-ое изменение генов под действием
радиации, химии и т.д.
1
Скрещивание (кроссовер)– это процесс образования ДНК потомка на основе частей ДНК родителей.
В рез-те последоват-го возд-я зтих 3-х процессов в природе осущ-ся адаптация, приспособленность видов, генетич-й отбор и т.д., которые позволяют живым существам достигать оптимальности за сравнительно небольшое число популяций. Поэтому основной сферой применения ГА явл-ся решение задач оптимизации, в которых ГА показаликачества не хуже самых оптимальных численных алгоритмов.
Структура ГА:
Построение ГА состоит в конструировании общей схемы, включающей набор перечисленных этапов, расположенных в определенном порядке.
Рассмотрим примерный вариант ГА.
∙Начальная популяция
∙Вычисление Fполез.
∙Отбор
∙Скрещивание
∙Мутация
∙Вычисление Fполез.
∙Отбор
∙Условие остановки
1 этап. Нужно сформировать начальную популяцию. С точки зрения предыдущей аналогии с ДНК каждый элемент популяции – это вектор, который содержит запись, причем длины всех записей одинаковы. На этом этапе можно выбрать 2 параметра модели: длина записи (сколько букв или цифр) d, кол-во элементов популяции N.
Выбор начальной популяции может быть случайным, в центре искомой области или аналитическим (по какому-то закону).
2 этап. На втором этапе мы считаем, что одни вектора лучше других. Чтобы это определить, вводится специальная
2
функция полезности (индекс сверху–номер вектора, индекс снизу–номер буквы вектора); результат вычисления
F (X k ) – положительное или равное нулю число. Можно
сравнить F(X k ) и F(X m ), т.е. ответить на вопрос: какая из
популяций полезнее. Функция полезности должна быть вычислена на втором этапе для всех элементов.
3 этап. Нужно отобрать N’ элементов, лучших среди всей совокупности N, т.е. N’<N. Мы должны выбрать максимальные или минимальные элементы популяции по значениям функции полезности. Выбор максимальных или минимальных определяется по соотношению N’ и N. Если N’ < N/2, то выгоднее выбирать максимальные, в противном случае - минимальные. Если больше худших, то выбираются лучшие; если больше лучших, то – худшие.
4 этап. Нужно определить число составляемых пар для скрещивания.
5 этап. Необходимо провести процедуру мутации, имеющую как минимум 2 параметра P и N’’’. После проведения мутации вновь проводят вычисление функции полезности и отбор лучших элементов.
После этого одна итерация алгоритма выполнена, теперь нужно проверить условие выхода-остановки. Это условие должно определять: достаточно ли этих итераций или необходимо выполнить ещё одну.
Возможны следующие варианты условия выхода:
1)Задается фиксированное количество итераций. Поскольку одна итерация – одно поколение, то задаём количество поколений (параметр KP), достигнув последнего поколения, завершаем процесс алгоритма.
2)Задаётся изменчивость поколений (Gизм).Это функция, которая определяется как разность лучшей функции полезности в N и N-1 поколениях:
Gизм=Fлуч(N)-Fлуч(N-1)
3

Таким образом. если мы видим, что от поколения к поколения полезность сильно не увеличивается и изменчивость мала, то можно прекратить этот алгоритм.
3) Задаётся необходимое условие для максимальной функции полезности (Fmax). Если в каком-то поколении Fmax будет превышено, то мы прекращаем вычисления. Иногда можно рассматривать условие для максимальной функции полезности для одного элемента (чемпиона) или для набора элементов (получено заданное количество качественных элементов).
Начальная популяция → Вычисление Fполез. → Отбор → Скрещивание → Мутация → Вычисление Fполез → Отбор → Условие остановки (например, достижение предельной популяции, когда наступает насыщение, т.е. популяция не изменяется).
Внутри j-того объекта популяции можно задать коэф-т мутации Смут, который будет измерять, много или нет эл-тов меняется.
Отбор:
Отбор можно добавить на каждом этапе ГА.
Отбор |
заключает |
в себе функцию эффективности ( |
|
γ = |
N0 |
N |
). Отбор эл-тов в поколении выполняется |
|
|
|
|
с пом-ю спец. функции, которая наз-ся функцией полезности. Чем > значение этой функции, тем лучше считается элемент.
Кроссовер:
Объекты популяции состоят из сложных эл-тов – аналогов генов (молекул нуклеотидов 4-х видов: А, Т, С, G). Это своего рода алфавит, на котором записывается текст сообщения ДНК. Как и в любом тексте важно, какие буквы и в какой послед-ти они следуют. Если поменять местами 2 нуклеотида, то это будет совсем другая особь.
4

Как известно, ДНК потомка образуетс из генов 2-х родителей – это парный кроссовер. (В теории тройной кроссовер). В природе только парный кроссовер:
Ax |
Ay |
|||
A |
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
Bx |
By |
|||
Вначале ученые моделировали кроссовер просто: брали ½ от объекта А и ½ от объекта В и соединяли в единого потомка. Получали как мин-м 4-е вар-та соед-я: AxBx, AxBy, AyBx, AyBy. Потом биологи док-ли, что гены передаются не поровну, тогда возникла идея модификации ГА, выбирая неравные части эл-тов. Модуляция кроссовера свелась к моделир-ю шим.
Теория шим:
Шимаангл. «маска». Идея: по 2-м родительским группам вычисляют потомка. Суть метода: если прорезать в некот-х клетках отверстия, то часть букв будет видна. Одни буквы берем у 1-го, другие - у 2-го родителя. Шиму можно промоделировать двоичным числом (1-открытая буква, 0- закрытая). Тогда маскаэто двоичное число (или 4-х битное число).
Наложение шимы
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
С |
помощью |
шимы мы уходим от вероятности. При |
|||
моделир-и шим только 2 пар-ра: k- выбор шимы и p- число прорезей в шиме.
Нейронные сети:
В настоящее время особое место в искусственном интеллекте занимает имитационное моделирование биологии человеческого мозга с помощью специальных моделей нейронов и нейронных сетей. Нейроны головного
5
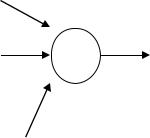
мозга образуют систему, которая обрабатывает поступающую от органов чувств информацию. У нейронов есть аксон (отросток), с другой стороны к нему подходят дендриты. Окончание на аксоне – синапс, который необходим для передачи инф-ции от 1-ой клетки к дендритам другой.
Нейрон–система, у которой есть несколько входов и один выход. Через дендриты информация проникает в нейрон:
дендриты
аксон
Усложнение системы состоит в том, что нейроны объединяются в виде пленки – сеть. Они обладают достаточной сложностью, чтобы производить прием сигнала. Был обнаружен пороговый характер нейрона (пока сигнал не дойдет до опред-й величины, нейрон его не передает). Так как входов у нейрона неск-ко и они поразному ослабляют сигнал, то j-тому входу можно
поставить соотв-щий вес. Тогда сигнал ослабления [0,1] .
Сигнал в большинстве случаев можно считать битом (0 – нет, 1 -есть), все входы можно считать большим двоичным числом, выходы - другим двоичным числом. действие сети
– преобразование больших двоичных чисел.
Эффекты: 1) нейрон способен уставать (есть фазы активности и пассивности); 2) между нейронами конкуренция, неработающие отмирают; 3) сигналы от разных дендритов могут мешать и помогать друг другу; 4) появл-ся эффет самосогласования.
Модели нейронов:
Свойства сетей зависит от каких нейронов она состоит. Т.к. можно придумать разные модели нейронов, то эти модели
6

стараются приблизить к биологии человеческого нейрона, здесь возникает сложность, т.к. эти объекты до конца не изучены.
1. Модель Персептрона.
Исторически первой моделью нейрона была модель Мак-
Uвых
1
Uвх 
Каллока и Питтса. Это была самая простая модель. Они назвали свою модель Персептроном. Как у нейрона у него несколько входов и один выход (входы синапсы, а выход – аксон).
Синапсы получают сигналы от аксонов других нейронов, а аксоны соединяются с синапсами других нейронов, и образуется многослойная сеть.
Так же как в природе у каждого синапса есть весовой коэф- т wi и сигнал xi , то сумма сигналов с разным весом
образует 1 сигнал – вх-й: |
Bx = |
å wi xi |
|
|
|
Wi |
|
|
xi |
|
|
Т.о. в персептроне входной сигнал – это сумма сигналов разного веса.
Персептрон может генерировать выходной сигнал, если
7
wi xi ³ U0 |
Þ |
Uвых |
= |
|||
å = í |
|
|
|
å |
|
|
ì |
1,U0 |
£ |
wi xi |
. Т.о. персептрон обладает |
||
ï |
||||||
ï |
0,U |
|
> |
å |
w x |
|
|
0 |
|
i i |
|
||
î |
|
|
|
|||
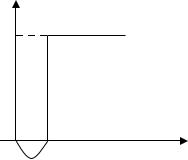
пороговым эффектом, т.е. сигнал на выходе получается только при достижении порога U 0 . Поэтому персептрон называют пороговым нейроном.
Uвых
1
0
Uвх
U0
Т. к. вход связан с другим нейроном j , то w зав-т от 2-х
величин: i – номер входа данного нейрона и j – др нейрон, с которым связан данный, тогда оценивая влияние на j-й
вход др нейрона, вводят yi: å wij xi yj .
Как правило, в моделях рассматривается вес 0 ≤ wij ≤ 1, i -
номер входа у данного нейрона, j - номер входа другого нейрона, x и y – значения только 0 или 1.
Если рассмотреть сеть из персептронов, то она похожа на двоичный автомат. Существуют методы анализа такого автомата с пом булевых ф-ций. Поэтому модель Мак- Каллока-Питтса стала самой распространенной.
2. Сигмоидальный нейрон.
В этом нейроне перешли от дискретной модели к непрерывной, где порог непрерывный( т.е. не только 0 и 1),
8

сигнал непрерывный. Нужно |
|
было подобрать ф-цию. |
||||||
Нашли такую: |
f (Uвх ) = |
|
|
|
|
1 |
|
|
1 |
+ |
e |
− β (Uвх − U0 ) |
|||||
|
||||||||
|
|
|
|
|||||
Чем больше β , тем быстрее дойдем до единицы. Т. е. при
β |
→ |
∞ |
мы стремимся к персептрону. Когда β =10; |
12 |
рез-ты |
ничем не огтличаются от персептрона. |
|
U вх |
≈ 0 . В персептроне параметры : веса и U0, здесь |
||
еще Uвх. сигмоидальный более четкий. Но ни персептрон, ни сигмоидальный не похожи на настоящий нейрон, их исследуют с целью получения более высокого соот-я с нейронной сетью.
3. Модель Видроу.
У этой модели две особенности: адаптивный подбор весовых коэффициентов и деление нейронов на два вида: аутстар и инстар.
-instar (в звезду)
-austar
В инстаре как у персептрона 1 выход, много входов. Аутстар – много выходов, 1 вход.
Получили нейроны разных типов, но в природе все нейроны одинаковы, одного типа, но они переплетены. Такое переплетение можно отразить с пом outstar’ов.
9
Замечание. Известно, что в природе нейрон может менять проводимость своих дендритов.
В видроу возможность самообразовываться введена в саму модель.
Этот алгоритм адаптивный и существует попытка приблизится к устойчивому состоянию сети. В аутстаре вводится не вес входящий, а вес выходящий, т. е. этот нейрон работает в обратном режиме.
Аутстары и инстары в видроу наз. Adaptive Linear Neuron (адаптивный линейный нейрон).
Очень часто с помощью адалайна моделируют процессы самообразования, самосагласования и даже появился термин: Many ADALINE (MADALINE) - сеть, состоящая из элементов типа ADALINE.
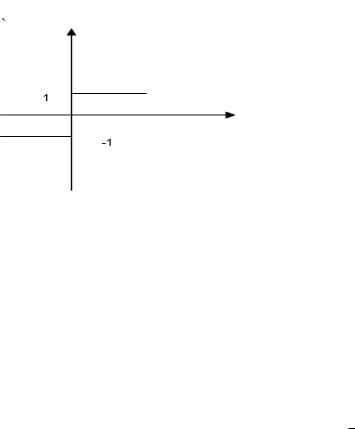
Причем характеристика ADALINE необычна: она пороговая, нет 0, на выходе либо +1 либо -1:
Т. о. Видроу формировал адалайны на основе логических операций no, and, or и мажоритарных соединений (когда сигналы равны на входе и на выходе).
Гроссберг был автором инстара и аутстара. У Видроу был просто адалайн с +1 и -1. Гроссберг придумал для своих инстар, аутстаров спец методы обучения, которые наз
методы обучения Гроссберга.
4. WTA (победитель получает все).
Эта модель конкурентной борьбы нейронов. Его идея: выходной сигнал формируется не на основе суммы
10
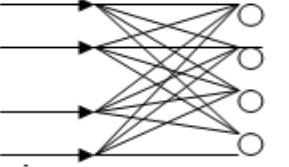
сигналов, а по результатам самого сильного сигнала (если сигнал преодолел порог, то он существует).
Одновременно нейроны WTA по аналогии с адалайном могут быть сформированы в группы конкурирующих между собой нейронов.
на входе сигналы делятся одинаково на все нейроны, дальше сигналы от всех нейронов сравниваются и на выходе один сигнал – победитель.
Т.о. появляются три типа WTA:
1)внутренняя конкуренция между входными сигналами
2)внешняя конкуренция между нейронами. Сигнал передается от выигравшего нейрона.
3)используется и внутренняя и внешняя конкуренция.
5. Нейроны Хебба.
Хебб долго изучал реальные нейроны нервных клеток, он изучал механизмы самосагласования клеток.
Варианты:
1)одна клетка подавляет другую (отрицательное действие).
2)одна клетка содействует возбуждению другой клетки (положительное действие).
3)клетки помогают друг другу (когда ни одна клетка не возбуждается отдельно, а вместе у них получается).
Хебб сделал вывод: изменение весов должно быть пропорционально произведению сигналов на 2-х моделях,
т.е. |
wij ~ yi y j . Если – |
wij , то сигнал |
|
отриц-й и они друг друга гасят. |
Если + |
wij , то |
|
сигналы помогают др другу. |
|
|
|
11
Вывод наз. правилом Хебба. Нейроны и нейронные сети, которые подчиняются правилу Хебба, называются Хеббовскими.Как и у Гроссберга правило Хебба дает возможность создать обучение, т.е. обучение по Хеббу. Хеббовскими наз нейроны, веса которых подбираются по правилу Хебба.
6. Стохастическая модель.
Это вероятностная модель. В данной модели рез-ты на выходе зависит не только от входящей информации, как во всех др моделях, но и от некой случ-й составляющей, случайности событий.
Сущ-ет неск-ко вар-тов введения в модель этой составляющей.
1.выход делают случайным, т.е. сигнал либо проходит либо запирается.
2.в модели сигнаидального нейрона может случайно
меняться параметр β , а в модели персептрона меняют U0
.
3. в модели может случайно отключаться (или вкл-ся) один их входов.
Замечание. В настоящее время во многих моделях нейрона вводятся понятия «активности» и «усталости». Передав сигнал (особенно в условиях конкуренции, WTA), нейрон отдыхает (становится неактивным), чтобы позже проявить активность Þ ввели параметр усталости: чем > сигнал на выходе, тем сильнее усталость. Т.о. у нейрона формируются фазы активности и усталости. Особенно важны эти фазы, где введено в модели нейронных сетей отмирание.
Виды нейронных сетей (НС):
НС образ-ся путемсоед-я однородных нейронов, т.е. нейронов одной модели, следоват-но, сети, например, персептронные, WTA, Гроссберга и т.д.
12
По построению сети делят на: 1)однослойные (нейроны образуют 1 слой);
2)2-хслойные (когда выходы из одной сетиэто входы для второй).
Двухслойные сети делятся на сети без обратной связи и сети с обратной связью.
3)многослойные сети (есть входной слой, выходной слой, 1 или неск-ко внутр. слоев).
Также посторение сети идет:
1)линейное соединение (слой за слоем);
2)рекуррентное (есть обратная связь между вх. и вых. слоем);
3)радиальная сеть (слои образуют окружность).
Особое место в НС заняли реккурентные сети (с обратной связью): обратная связь бывает положит-ая (делает систему неустойчивой, т.к. усиливает отклонение от равновесия) и отрицат-ая (делает систему более устойчивой, ее очень трудно отвести от равновесия). реккурентная сеть с режимом обратной связи была использована для разработки спец. памяти, которая наз. BAM (… assotiation memory)- ассоциативная память, хар-на тем, что запоминает знания, а не данные (например, в рисунках, фотках).
Особые виды НС:
1. Сеть с самоорганизацией (WTA сети, …), когда в сети
ярко выражена саморг-ция: периоды отдыха и активизации, конкуренция групп и отмирание нейронов. (самоорг-ция за счет обратной связи сюда не входит). Кохонен придумал правила самоорганизации, конкуренции, самообучения в НС.
2. Корреляционные сети (сети Хебба) – это самооргщаяся сеть, но на основе правил Хебба. Делятся на 2 категории: PCA (компонентный анализ) и ICA (анализ независимых компонент).
13
3. Нечеткие (случ-е) сети - используют нечеткую логику. Прохождение сигнала через случ-й нейрон опр-ся не только уровнем сигнала, но и случ. величиной. Если случ-е нейр-ы объед-ся в сети, то образ-ся очень сложная случ-ая система, которая наз. случайными сетями. Здесь есть алгоритмы самоорг-ции, но особого вида.
14
32.Экспертные системы: структура, назначение, классификация. Методы построения экспертных систем. Понятие о инженерии знаний.
ЭС – система моделирующая поведение человека-эксперта в какой-то области знаний Современные ЭС создаются на основе баз знаний,
используют интеллектуальный интерфейс, интеллектуальные подсистемы вывода ответа на запрос, использующие нечеткую логику и интеллектуальный анализ данных. Для работы и обслуживания ЭС даже введен специальный инженер по знаниям, который должен следить за качеством используемых знаний.
Общая харак-ка, назначение ЭС.
На сегодняшний день самое важное – сфера создания экспертных систем.
Часто формируют динамическую часть БЗ.
Внастоящее время ЭС не мыслятся без СО. СО служит для модернизации всех структур ЭС. СО формируется как отдельная система, тогда когда ней используются средства построения и добычи знаний.
Знанияне просто факты, их нужно обрабатывать и сжать.
Всовременных системах стремятся перейти к естественному интерфейсу.
Назначение ЭС
Моделировать работу человекаэксперта. Ему задают вопросы он выдаёт ответ. Вопрос должен быть формализован. Их принято называть запросами.
Запросы, которые можно подавать ЭС, определяют её область применения. Чем шире эта область, тем больше применения ЭС, но теряются скорость и точность работы. ЭС строит ответы на вопросы исходя из соей БЗ.
При создании ЭС существует этап заполнения БЗ. И предусматривают какойлибо метод накопления, обработки, совершенствования и оптимизации знаний.
15
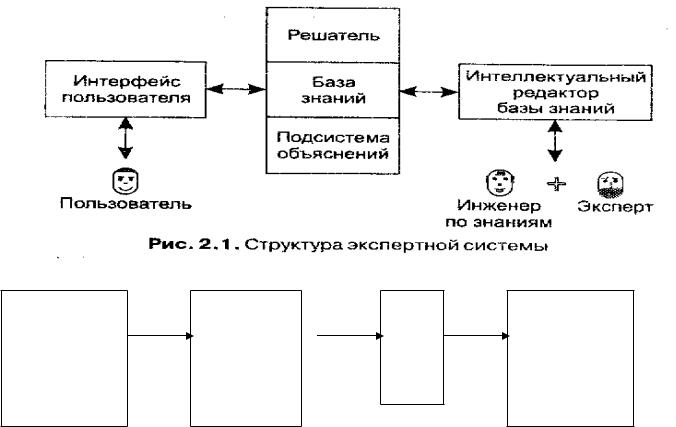
Наилучший вариант самообучения, но приходится иметь инженера знаний.
Пользователь – это человек, который получает информацию от экспертной системы, а так же может закладывать факты и правила в эту систему.
Интерфейс – это программа, которая обеспечивает взаимодействие пользователя с экспертной системой (ввод, вывод информации).
Общая схема ЭС:
Структура экспертной системы.
Интерфейс |
Механизм |
База |
Система |
пользователя |
Логического |
знаний |
Машинного |
|
вывода |
|
обуче- |
|
|
|
ния |
1.Пользовательчеловек; который получает сведения из ЭС, и может закладывать факты и правила в ЭС.
2.Интерфейспрограмма, которая обеспечивает взаимодействие пользователя с ЭС.
3.МЛВнабор правил, которые позволяют строить ответы на запросы со стороны интерфейса обращается к БЗ.
4.БЗнабор правил и фактов, которые не вошли в МЛВ. МЛВ и БЗ взаимно обмениваются информацией. МЛВ может изменить, удалить, добавить факты.
База Знаний
Зависит от модели представления знаний
16
Для логической БЗ (Пролог) состоит из набора сущностей: Факты – связывают константы Правила – связывают элементы с помощью условия
Механизм логического вывода (МЛВ) – набор правил, которые позволяют строить ответы на запросы со стороны интерфейса. За необходимыми данными этот блок обращается к базе знаний. БЗ – набор фактов и некоторых правил, которые не входят в МЛВ. МЛВ и БЗ взаимно обмениваются информацией – это значит, что МЛВ может изменить, удалить или добавить какие-то факты. Часто для этого формируют динамическую часть БЗ.
Системы Обучения – система обучения. В настоящее время экспертные системы содержат системы обучения. Она служит для модернизации структур всей системы: изменения интерфейса, механизма ввода, вывода БЗ. СО формируется как отдельная система тогда, когда в ней используются средства построения и добычи знаний. Т.е. знания это не просто факты, их еще необходимо обработать и сжать в виде спец-х правил.
Интеллектуальный интерфейс
Всовременных системах стремятся перейти к естественному интерфейсу, близкому человеку (естественный язык, восприятия образов, интеллектуальный диалог).
ЭС задают вопросы, она выдает ответ. Вопрос\Запрос должен быть формализован (построен по определенным правилам).
Интелектуальный анализ данных
ВИАД 2 основные технологии:
Раскопка знаний\данных: Data Mining – это переработка большого объема данных с попыткой выявить взаимосвязь (ассоциативные методы анализа, логические методы – дедукция, индукция, абдукция).
17
Открытие знаний\данных: KnowLeadge Discovery – обобщение, кластеризация и классификация знаний.
Интеллектуальные ЭС.
Наибольшее развитие получили ИИС. Сравним интеллектуальные ИС (ИИС) и обычные ИС. Их отличия: 1. Изменение интерфейса. Стараются сделать его интеллектуальным. Здесь интерфейс активный, т. е. инф. Система становится агентной системой. Агент – это развитие понятия «объект». Объект, также как и фрейм соединяет в себе св-ва и методы, с пом. которых можно изменять эти св-ва и выполнять какие-то действия. Т. О. объект может реагировать на события(событийное управление). Агент дополнительно к этому имеет внутренние методы, которые побуждают его к действию – сбор фактов и изучение ситуации, приспосабливание к ситуации, установление контактов с др. объектами и пользователями, стремление к некой сверхзадаче. На сегодн. день сущ как одноагент., так и многоагентные системы. Интерфейс информац-ой агентной системя отл. тем, что агентная система не просто отв. На вопросы, но и сама стремится задать уточняющий вопрос и т. д.
2. Изменение структуры данных. Расширяются формы представления данных, т. е. помимо стандартных моделей появляются новые модели данных. Принято разделять данные на БД и БЗ. БЗ – набор правил, с пом. которых м. разыскивать данные в БД. Принято формировать БЗ в виде хранилища данных. Хр. данных характерно для СУБД ORACLE, Informix. В каждом хранилище данных сущ. программа, кот. Обрабатывает данные и формирует БЗ по двум осн. технологиям: раскопки знаний, открытие знаний. Разница между технологиями определяется методами правил БЗ. Раскопка знаний наз. OLAP и Data Mining. Открытие – Knowledge Discovery. Data Mining – перерабатывание большого объёма данных с попыткой
18
выявить взаиамосвязь; откр. знаний – это значит установить скрытую связь. Кроме программы обработки в хранилище данных важную роль игр. Формирование структуры БД. Как известно, сущ. так называемые правила нормализации данных. Следующим этапом является формирование такой структуры, чтобы не только был мин. объём информации, но и самый быстр. поиск. теоретически самый быстр. поиск идёт по бинарному дереву. Но практически иногда выгодны др. формы. Характерные формы: звезда, созвездие, дерево.
3. использование методов системного анализа для инженерии знаний. Хранилище данных должно пополняться, оптимизироваться и т. д. Сами данные часто обрабатываются, чтобы отделить несущественные. Поэтому между источником данных и хранилищем сущ. система, кот. наз. системой облучения. Она м. б. автоматич. или управляемой. Задача инженера знаний: собирать данные, кот. имеют практическую значимость, а также формировать и модифицировать БЗ дополнительно. инженер знаний должен: а) опр-ть источники информации; б) опр-ть достоверность и активность инф-ии; в) формировать правильные правила для БЗ. Решить эти задачи м. только профессионал в этой области. Но областей много, а инж. знаний д. б. ещё специалистом по экспертным системам, значит он пользуется спец. методом экспертных оценок.
4. Деление БД и БЗ на статистич. и динамич. составляющую.Первые варианты использования динамических структур (хэш-памяти) использовались ещё в обычных ИС, но в хранилищах данных эти технологии значительно усовершенствовались. Вся структура данных динамич. Части, ресурсы сервера храеилища данных ориентированы на оптимизацию динамической части, т. к. она хранится в оперативной памяти. В оперативной памяти
19
в осн. отправляется БЗ. т. к. там самые ёмкие данные. Т. О. ИИС становятся настолько сложными системами, что практически не сущ. вариантов подобных СУБД общего назначения. Это всё специализированные, но не специализированы они не в области знаний, а по решаемым задачам. Зад. прогноза, зад. динамич. оптимизации, ситуации неопределённости и т. д. Кроме того, особую область занимают агентные и мультиагентные системы, которые могут служить основой робототехники и т. д. , т. е. для особых задач.
Методы построения ЭС и классификация ЭС по методам построения
ЭС принято классифицировать либо по назначению, либо по принципу организации.
Классификация по принципу организации
1)интеллектуальные ИС 2)системы поиска на основе семантических сетей и
тезаурусе. Иногда их наз-ют интеллектуальнопоисковые системы.
3)Системы, построенные на нейронных сетях. Начиная с 1998 года, стали выпускаться промышленные образцы ассоциативной памяти на нейронных сетях, системы обработки инф-ции на нейронных сетях.
4)Система основанная на распознавании образов. Здесь активно используется кластерный анализ, интересны также разработки в области когнитивной графики, т.е. графики, которая может адаптироваться.
5)Агентные и многоагентные системы, которые не относятся к информационным системам.
6)Системы, основанные на случайных характеристиках: байсовских сетях, сетях Петри. Случайными характеристиками могут обладать и нейронные сети. Главное, что объединяет эти сети – использование
20

нечеткой логики, они называются нечеткими системами.
7)Фреймовые системы. В настоящее время идет соединение фреймовых и агентных систем.
8)Системы основанные на декларативном подходе (логическое или функциональное программирование). Здесь выделяют логические системы и системы, основанные на структурных данных. В логических системах необходимо: а) построить аксиоматику, т.е. выделить положения аксиом, которые играют роль фактов; б) установить правило логического вывода, заключений с помощью которых из аксиом можно доказать другие утверждения; в) сформировать интерфейс запросов.
Классификация по назначению ЭС.
1)информационные системы позволяют отвечать на вопросы в рамках существования информации. Для данных систем можно использовать любые подходы, но в основном это логические системы, структурные и нейронные системы.
2)Аналитически поисковые системы: в них используются поисковые системы и системы распознавания образов. Особые направления в данной области – это развитие систем ассоциативной связи (ассоциативная обработка информации с помощью нейронных систем, нечетких систем и сетей добытия знаний ИАД – интеллектуальный анализ данных).
3)Направление работы с естественным языком, т.е. ЭС в области языка: переводчики, проверка правописания и др. Они основаны на методах распознавания образов, семантических сетях, нечетких системах.
4) Системы прогноза:: |
задача |
– построить |
экстраполяцию текущих |
данных, |
основываясь на |
обработке текущей информации. Суть экстраполяции:
21
чем больше используются данные о предшествующих событиях, тем точнее возможна экстраполяция. Главная проблема – правильно выбрать нужную информацию: чтоб она было min и значимой. Здесь используется ИАД; попытка оценить вероятность тех или иных будущих событий. Т.о. необходимо просматривать варианты будущих событий и отображать наиболее вероятные. Здесь важную роль играют нейронные системы, генетические, нечеткие системы. Особую роль играют в таком анализе байсовские сети, которые так удобны для решения этих задач, долгое время они являлись лидером.
5)Системы управления являются продолжением систем прогноза, для этого необходимо на основе прогноза строить обратную связь, т.е. добавить в систему обратные связи. В формировании обратной связи особую роль играют ИАД, рекуррентные, нейронные сети, логические системы.
6)Системы принятия решений: это усовершенствованные системы управления. Если есть системы управления, действия системы и системы прогноза, то можно строить не только корректирование системы управления, но и системы собственного вектора. Система принятия решений переводит самостоятельные и функционированные ЭС на новый уровень.
7) Системы самостоятельного поиска и самоорганизационные системы: на основе агентных систем можно усовершенствовать и систематизировать принятия решений, сделав ее на много самостоятельной. Агентные системы обладают неким подобием свободы воли, т.е. они обладают возможностью адаптироваться к ситуации, общаться и
22
учиться и формировать свое поведение на основе неких правил общения.
8)ЭС логического анализа: с 40-х годов, с тех пор как были созданы искусственные логические системы, идет постоянное усовершенствование таких систем. Перед ними становятся следующие цели: а) заменить человека в такой рутинной деятельности как математические преобразования, доказательство теорем (системы ТРНЗ, их целю была разработка конструктивной изобретательной и научной деятельности); б) решение сложных логических задач и компьютерных игр.
9)ЭС в области классификации: одним из направлений деятельности человека– классификация: распознавание, систематизация защита, диагностика. Проблемы диагностики с одной стороны сложны, с другой–важны, ЭС в диагностике получает свое собственное развитие. Системы диагностики прежде всего основаны на ИАД и системах распознавания образов (в ИАД есть особое направление – методы классификации).
Инженерия знаний
Усложнение процессов разработки, внедрения и сопровождения ЭС привели к появлению особой специальности – инженер знаний. Инженерия знаний – особый раздел инженерной деятельности, связанный с обслуживанием баз знаний.
При использовании интеллектуальных систем для решения задач в данной предметной области необходимо собрать о ней и создать концептуальную модель этой области. Источниками знаний могут быть документы, статьи, книги, фотографии и многое другое. Из этих источников надо извлечь содержащиеся в них знания. Этот процесс может оказаться достаточно трудным, ибо надо заранее оценить
23
важность и необходимость тех или иных знаний для работы интеллектуальной системы. Специалисты, которые занимаются всеми вопросами, связанными со знаниями, теперь называются инженерами знаний. Эта новая профессия порождена развитием искусственного интеллекта.
Значительная часть профессионального опыта остается вне источников информации, из которых инженер вносит знания в интеллектуальную систему, в головах у профессионалов, не могущих словесно их выразить. Такие знания часто называют профессиональным умением или интуицией. Для того, чтобы приобрести такие знания, нужны специальные приемы и методы. Они используются в инструментальных системах по приобретению знаний, создание которых одна из современных задач инженерии знаний.
Полученные от экспертов знания необходимо оценить с точки зрения их соответствия ранее накопленным знаниям и формализовать их для ввода в память интеллектуальной системы. Кроме того, знания, полученные от различных экспертов, надо еще согласовать между собой. Все эти задачи и выполняет инженер по знаниям.
24
33.Математические модели в физике, химии, биологии и экономике
Мы будем рассматривать в данном разделе аналитические модели. В аналитических моделях вход. и выход. Параметры связаны явными выражениями: уравнениями, неравенствами и т.д. Если мы решаем системы уравнений Колмогорова-Эрланга, это аналитическое моделирование, если же мы останавливаемся на графовой модели и проводим статистический эксперимент, определяем как обслуживает система поток заявок, то это имитационное моделирование. Для решения аналитической модели обычно приходится применять численные методы решения задач, но некоторые модели дают и аналитическое решение, т.к. для решения разных математических задач используются разные методы, иногда аналитические модели делят по методам (интегральные, дифференциальные, линейные и т.д.), но обычно по сферам применения (физические, химические, биологические, педагогические, технические). Рассмотрим некоторые примеры аналитической мат. моделей, которые являются наиболее простыми и в то же время классическими.
Математические модели в физике и технике
В физике моделирование в основном используется для описания процессов в производстве, связанных с решением дифференциальных уравнений и частных производных. Все другие модели, это обычно упрощенный вариант этих процессов. Основой для построения моделей являются следующими законами и уравнениями:
∙ Δυ =0 - уравнение Лапласа( – 2-ая
производная)(описывает поведение электрических и магнитных полей, упругость);
25

∙
∙
∙
∙
Δυ = ρ(x, y,z) -уравнение Пуассона(используется в
механике); |
|
|
∂2 T |
=aΔT - уравнение теплопроводимости; |
|
∂ t |
|
|
∂2 υ |
=CΔυ |
- волновое уравнение, это частным |
∂t2 |
||
|
|
|
случаем может быть названо уравнением колебаний.
= |
∂ 2 |
∂ 2 |
∂ 2 |
|||
|
+ |
|
+ |
|
- оператор Лапласа в декартовой |
|
∂ x2 |
∂ y2 |
∂ z2 |
||||
системе координат.
Часть уравнений записывается в одномерном виде или с помощью радиус-вектора
|
|
|
|
|
|
|
d 2 |
|
|
|
|
|
d |
|
|
|
r |
||
|
|
|
r |
|
a = |
||||
ν = |
; |
||||||||
dt |
dt 2 |
||||||||
2. Модель колебательной системы
Рассмотрим ее от простого к сложному. В качестве примера могут служить очень многие окружающие на предметы, где важна вибрация (двигатели). Колебания свойственны и электрическим системам. Будем считать, что у нас одномерные колебания (вдоль одной оси).
Положение предмета
определяется одной координатой х, уравнение будет
∂2 x + cx = 0 .
∂t 2
26
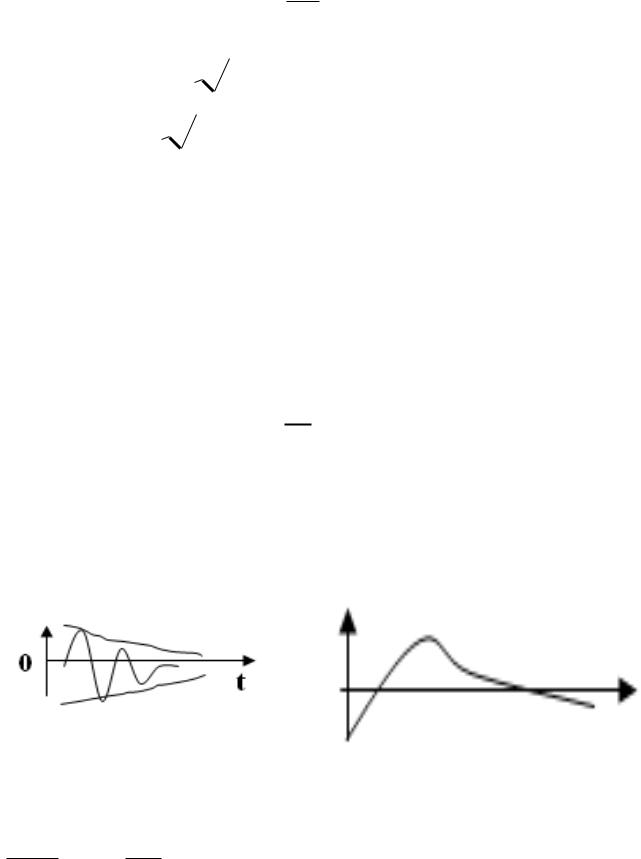
Решение этого диф. уравнения хорошо известно, оно представляет из себя
x = Acos( 
 ct) +
ct) +
+ Bsin( |
|
|
|
|
|
ct) = |
|||
~ |
|
|
|
|
ct + ϕ ) |
||||
Acos( |
||||
Колебания Гармонические со сдвигом фазы, незатухающие.
Усложняем модель - вводим затухание
d 2 x |
+ K |
dx |
+cx = 0 (К- коэффициент затухания) |
|
dt 2 |
dt |
|||
|
|
Если К мало (К<<1), то решение не будет сильно отличаться. Решение системы приводит к возникновению
x = Ae− kt cos( 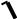
 ct +ϕ ) .
ct +ϕ ) .
К=0,1- затухание хорошо видно (переодич.). При увеличении К ( ≈ 1)- апериодическое затухание, когда нет ни одного периода.
Дальше Усложняем задачувведение периодичность внешней силы
∂∂ t2 2x + K ∂∂ xt + cK = βcos(pt)
27

Собственная частота ω= 
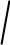 c , частота внутри силы р. Когда частоты равны, получаем резкое увеличение амплитуды колебаний - резонанс, ω= p . Если
c , частота внутри силы р. Когда частоты равны, получаем резкое увеличение амплитуды колебаний - резонанс, ω= p . Если
резонанс производить при колебании, собственные колебания затухнут, останутся вынужденные с частотой вынужденной силы.
К<<1, W>>p.
Модуляция. Внутри собственные колебания, их амплитуда моделируется с частотой собственных колебаний (биения)
Если К<0, м.б. β=0 (т.к. она только мешает) – параметрический резонанс.
Фактически параметрический резонанс при отрицательном затухании - это получение энергии извне. Процессы собственных колебаний важны, когда колебания паразитные (вредны), когда делают демпферы (делают затухания апериодичными).
Пример: рессоры автомобиля (обычно полезны для раскачки колебаний).
28

Резонанс может быть отрицательным и положительным по значению. Излучение электромагнитных волн основано на резонансах, как обычных, так и параметрических. Излучение и прием электромагнитных волн резонансные. Параметрический резонанс выгоден тем, что гораздо мощнее обычного. Это удобное средство для генерации, например, СВЧ-колебаний (магнитофон). Для параметрического резонанса собственная частота не нужна, поэтому можно вкачивать энергию до самого разрушения этого резонатора. Но может быть и вред, разрушение, что неприятно.
Модуляция – основа радиосвязи. Есть несущая частота, которую модулируют, а потом де модулируют. Звук низкочастотен (36 КГц), а радиоволна распространяется на высокой частоте, значит, нужны мегагерцы. Есть амплитудная, фазовая и частотная модуляция. Эффект биений обычно вредный, мешающий – это источник шума. Иногда с помощью биений делают специальные шумовые генераторы.
Модель теплопроводности тонкого слоя
Т1 |
|
Т2 |
|
|
|
ab
 X
X
стекло |
(тонкое, длинное), |
|
Т (t,λ ) - температура будет |
||||
|
|
|
∂ T |
∂ 2T |
t1 x = 0 = T2 |
||
равномерна, следовательно |
|
= a |
|
. |
T (t1 x = t) = T1 |
||
∂ t |
∂ x2 |
||||||
гранич. |
T (0, x) = T3 (x) |
Обычно |
это |
уравнение не |
|||
29
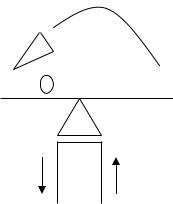
решается в явном виде, а с помощью клеточной аппроксимации. Решая эту систему уравнений, мы находим значения в узлах сетки. Подобным же способом моделируются другие задачи теплопроводности, электростатики и электродинамики. Основная проблема – сложность вычисления, поэтому требуются мощные ЭВМ. Еще одна модель – движение тела, брошенного под углом к горизонту. Для ее решения используют так называемый метод стрельбы, он уже близок к имитационному моделированию.
Еще – модель движения ракеты:
Mg |
F тяги |
|
|
|
|
|
|
m = m0 |
- α × t |
|
d 2 h |
F |
F |
− mg − KV 2 |
|
||||
|
|
|
|
|
тяги |
|
- |
уравнение |
dt 2 = |
m = |
|
m |
|
||||
Циолковского.
Кинетические и структурные модели в химии
В химии в основном распространены модели химических реакций и строение модели хим. соединений. Для хим. реакций самое важное –кинетика, т.е. изменение течение реакций со временем, т.е. чем быстрее идет реакция, тем меньше остается реагирующего вещества, и наоборот. В начале ХХ века Адольф Лотка сформулировал модель кинетических реакций, которая была названа модель Вольтерра-Лотки. Цепочка превращений веществ:
30

|
|
K |
K |
K |
® |
B _ |
|
|
A ¾ ¾0 ® |
X ¾ ¾1 ® |
Y ¾ ¾2 |
|
|||||
где _(K0 , K1, K2 - скорости) |
|
|||||||
|
∂ x |
=K 0−K 1 XY |
|
|
|
∂ y |
=K 1 XY −K 2 Y |
|
|
|
|
|
|
||||
|
|
|
|
|
∂t |
|||
|
∂ t |
|
|
|
|
|
||
∂∂Bt = K 2 Y
Получена система диф. уравнений. Эти уравнения по смыслу похожи на уравнения КолмогороваЭрланга. Это показывает, что то были тоже кинетические уравнения и все кинетические процессы похожи друг на друга.
В химии кинетические уравнения усложняются тем, что величины K 0 , K 1 , K 2 не являются постоянными, а зависят
от таких величин как t , p ,
химический состав веществ (температура подчиняется закону теплоемкости, р зависит от диффузии, которая
определяется уравнением ΔN + B ∂∂Nt = 0 - закон диффузии
Фика. Похожее соотношение имеет и закон фильтрационного переноса Дарси). В результате приходится решать одновременно с кинетической еще и эти сложные уравнения.
В химии большое значение имеют структурные модели молекул: Н-О-Н, особенно удобна для органических веществ (у них очень сложная структура).
При изучении нового хим. вещества делают новый хим. анализ - определяют пропорции содержащие тех или иных
31
веществ. Тогда можно определить из каких атомов состоит молекула, но и от того, как они соединены. Вводится валентная связь. Одни атомы имеют 1-ю валентную связь, другие 2-ю и т.д. Были обнаружены изомеры вещества с одинаковым количеством молекул, но с разными свойствами.
Þ2 задачи:
Определить внутреннюю структуру молекулы и связать ее структуру и хим. свойства, т.е. изучение изомеров.
Проектирование изомеров - научиться создавать устойчивые структуры для молекул различных видов и давать их предположит. свойства.
Обе эти задачи стали настолько популярны в органической химии, что даже были созданы специальные системы моделирования молекул.
Математические модели в биологии
Биология чрезвычайно связана с химией и биохимией => структурное моделирование из химии перешло и в биологию. Биологические структуры – очень сложные химические структуры => появилась наука биохимия, которая изучает химию биологических структур. Здесь методы структурного моделирования оказались очень полезны. Наиболее известные задачи, связанные с моделированием генов.
Гены – молекулы, из которых формируется так называемые информационные компоненты живых существ-ДНК, РНК. В основном гены уже изучены и известны, но остались вопросы какие гены входят в ту или иную ДНК и как они связаны между собой. Т.к. даже в простейшем ДНК генов десятки тысяч, возник мировой проект «модель ДНК» , сначала у простейших существ, теперь человека (завершение) . Структурное моделированиеведущее в биохимии.
32
Модели внутривидовой борьбы
Особи одного вида конкурируют между собой. В начале, когда особей мало, а условия благоприятные идет быстрый рост популяции, ограничения наступают из-за борьбы между особями одного вида. Самой первой простой моделью стала модель роста – модель безудержного роста. В этой модели отсутствует внутривидовая конкуренция, она будет модернизироваться.
Ni+ 1 |
= |
|
Ni * R |
||
1 |
+ aNi |
||||
|
|
||||
Чем больше a, тем меньше рост, однако, и эта модель не могла описать некоторые явления, которые возникали в реальных экосистемах. В некоторых системах возникали колебания численности из года в год. Ввели еще один параметр, усложнили модель
Ni+ 1 = |
Ni * R |
1+ (aNi )b |
Коэффициент b определяет нелинейную зависимость скорости роста R от численности. Численное изучение этой модели позволило обнаружить 4 характерные ситуации:
- монотонный рост
- ситуация затухающих колебаний
- ситуация незатухающих колебаний
- ситуация флуктуаций (случайных изменений) Данные модели дискретные, но можно построить и
непрерывную, кинетическую, ее уравнение:
dNdt = rM . при этом r – некий аналог скорости. Эта
двухпараметричная модель называется логистической кинетической моделью (модель Вольтера - Лоттки).
33
Модели межвидовой конкуренции
Если сосуществуют 2 вида, которые активно воздействуют друг на друга, то возникают процессы межвидовой конкуренции и борьбы. Наиболее известна модель (кинетическая) Вольтера - Лотки конкуренция двух видов:
dN1 |
= rN1 * |
(k1 − N1 ) − α 12 N2 |
||
dt |
|
|
k1 |
|
dN2 |
= rN2 |
* |
(k2 − N2 ) − α 21 N1 |
|
k2 |
||||
dt |
|
|
||
Коэффициенты определяют связь между 2 видами. Если, то увеличение особей второго вида идет к уменьшению особей первого вида. Второй вид подавляет первый. Если, то особи второго вида не влияют. Очевидно, чем больше волков, тем меньше зайцев. В модели 6 параметров – ее изучение очень сложно, поэтому обычно фиксируют часть параметров. В общем случае изучение этой параметрической модели показало, что популяции хищников и жертв испытывают циклические изменения. В биологии очень часто используют так же имитационное моделирование.
Имитационное моделирование в биологии Модель «жизнь»
В ней имитируется размножение простейших существ, задаются некоторые ограничения на размножение, гибель и т.д., а затем запускается эксперимент и прослеживается динамика со временем. Простейший вариант (школьный). Берем таблицу клеток пустых и заполненных (живых). Задаются правила, например если живая клетка окружена 4 и более живыми, то она погибает от перенаселения, если
34
возле нее один или нет, погибает от одиночества. Если к мертвой примыкает 3 живые, она оживает. Эксперимент:
-задается начальная случайная конфигурация живых клеток
-задается количество моментов времени, которое будет прослежено
-в цикле по моментам времени производят обновление таблицы по заданным правилам, и наблюдают за изменением картинки. Подобные системы изучались, и оказалось, что в такой таблице могут существовать устойчивые конфигурации, которые не разрушаются.
Модели в экономике
Экономические науки – одна из наиболее важных сфер применения моделирования, именно здесь модели дают наибольшую эффективность, например если оптимизировать в одной модели траты всего государства, эффект будет выражаться в миллиардах долларов. Можно выделить следующие типы моделей:
- модель ЛП (линейные) – модель ресурсов, запасов и
т.д.
- модели, построенные на транспортной задаче (распространение и перевозка грузов)
- модели целочисленного программирования (результат принадлежит области целых чисел, количество человек, число заводов и т.д.) – модели первого типа с целочисленными параметрами.
- модели динамического программирования – в основном связанные с развитием какого-либо производства, фирмы и т.д.
- игровые модели, связанные с противоборством, конкуренцией.
- прогностические модели, связанные с прогнозом ситуации при недостатке информации или случайных событиях.
35
- модели автоматического управления (сделать систему управления оптимальной)
нелинейные модели решаются только в отдельных случаях.
36
34. Стохастическое моделирование. Метод МонтеКарло в моделировании. Генерирование случайных и псевдослучайных чисел. Методы и алгоритмы генерации. Генерирование случайных чисел распределенных по экспоненциальному, нормальному и произвольно заданному закону распределения.
Стохастическое программирование – раздел математического программирования, совокупность методов решения оптимизационных задач вероятностного характера. Это означает, что либо параметры ограничений (условий) задачи, либо параметры целевой функции, либо и те и другие являются случайными величинами (содержат случайные компоненты).
Оптимизационная задача - экономико-математическая задача, цель которой состоит в нахождении наилучшего распределения наличных ресурсов. Решается с помощью оптимальной модели методами математического программирования, т. е. путем поиска максимума или минимума некоторых функций при заданных ограничениях (условная оптимизация) и без ограничений (безусловная оптимизация). Решение оптимизационной задачи называется оптимальным решением, оптимальным планом, оптимальной точкой.
Случайные величины характеризуются средними значениями, дисперсией, корреляцией, регрессией, функция распределения и т.д.
Статистическое моделирование – моделирование с использованием случайных процессов и явлений. Существует 2 варианта использования статистического моделирования:
– в стохастических моделях может существовать случайные параметры или взаимодействия. Связь между
параметрами носит случайный |
или очень сложный |
характер. |
|
37
– даже для детерминированных моделей могут использоваться статистические методы. Практически всегда используются статическое моделирование в имитационных моделях Модели, где между параметрами существует однозначная
связь и нет случайных параметров называются
детерминированными.
Детерминированные процессы – определенные процессы, в которых всякие процессы определены законами.
Человек считает все процессы детерминированными, однако со временем обнаружены случайные процессы. Случайный процесс – это такой процесс, течение которого может быть различным в зависимости от случая, причем вероятность того или иного течения определена.
Исследование процессов показало, что они бывают 2-х типов:
а) Случайные по своей природе процессы; б) Очень сложные детерминированные процессы;
Доказана центральная теорема, в соответствии с которой сложение различных процессов увеличивает случайный характер. Так, если сложить совершенно разные последовательности, не связанные между собой, то результат в пределе стремится к нормальному распределению. Но известно, что нормальное распределение – независимые события, следовательно, объединение детерминированных событий в пределе ведет к их случайности.
Т.о. в природе не существует совершенно чисто детерминированных процессов, всегда есть смесь детерминированных и случайных процессов. Действие случайного фактора называется “шумом”. Источники шума
– сложные детерминированные процессы (броуновское движение молекул).
38
Вимитационном моделировании часто сложные процессы заменяют случайными, следовательно, для того чтобы сделать имитационную модель, нужно научиться моделировать случайные процессы методами статического моделирования. Представляют случайные процессы в КМ последовательностью случайных чисел, величина которых случайно меняется.
Встатистическом моделировании очень часто используется метод статистических испытаний МонтеКарло. Метод Монте-Карло – это численный метод
решения математических задач при помощи моделирования случайных величин.
Суть метода: для того, чтобы определить постоянную или детерминированную характеристику процесса можно использовать статический эксперимент, параметры которого в пределе связаны с определяемой величиной. Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину
X , математическое |
ожидание |
которой |
равно |
a : |
||||
M( X ) = a . Практически же поступают так: производят |
n |
|||||||
испытаний, в результате которых получают |
n |
|||||||
возможных |
значений |
X ; вычисляют |
их |
среднее |
||||
арифметическое |
x = |
(å |
xi )/n |
и принимают |
x |
в |
||
качестве |
оценки |
(приближенного значения) |
a* |
|||||
искомого числа a |
: a ≈ |
a* = |
x . |
|
|
|
|
|
Рассмотрим суть метода на примерах его использования:
39
1) |
проверка |
равномерности |
|
распределения |
|
генератора |
|
случайных чисел. |
|
В |
статическом |
моделировании |
|
принято источники |
|
случайных чисел называть
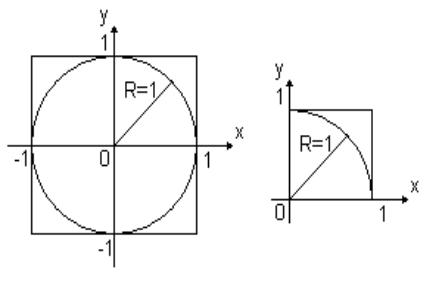
генераторами. Обычно используют генератор случайных чисел равномерно распределенных на диапазоне от 0 до 1. Распределение называется равномерным, если вероятность появления числа на любом из отрезков одинакова. После создания генератора можно проверить, насколько равномерно его распределение. Это можно сделать методом Монте-Карло. Рассмотрим ПДСК (x;y) и построим окружность R=1. Вокруг окружности построим квадрат. Рассмотрим первую четверть:
Найдём площади квадрата и окружности: Sкв.=1; Sчасти кр.= Sкр./4=πR2/4=π/4.
Проводим статистический эксперимент, для этого генерируем 2 последовательности xi [0;1] и yi [0;1] .
Пара этих чисел дает точку на плоскости (xi , yi ) . Т.о.,
эти две последовательности дают последовательность точек, но часть точек попадает в окружность, а часть будет вне окружности. Подсчитываем количество точек внутри Nвн. и общее количество точек Nобщ.. С точки зрения теории вероятности, если множество точек равномерно распределено по площади, то кол-во точек зависит от размера площади:
40

Nlimобщ → ∞ |
Nвнутри |
= |
Sсектора |
= |
π |
|
|
4 . |
|||
Nобщее |
Sквадрата |
Проверяем, так ли это в нашем эксперименте. В принципе точно π/4 мы не получим, но должны получить число близкое к нему. Проводят несколько экспериментов, а потом найденную величину усредняют.
Если средняя величина ближе к π/4, чем каждое из вычисленных величин, то считают, что гипотеза о равномерном распределении оказалась правильной. Для метода Монте-Карло это характерно: делаем гипотезу, затем проводим статистический эксперимент и проверяем эту гипотезу. Если гипотеза справедлива, то распределение равномерно, в противном случае – не равномерно.
2) Вычисление интеграла.
xx(), где S+ - площадь под кривой, там где функция >0.
S− - площадь под кривой, там где функция <0.
41
Рассмотрим прям.1 и проведем в нем эксперимент, найдем S+ . Проведем эксперимент в прям.2 и найдем S− .
Потом можно найти интеграл. Основания прям. одинаковые (от a до b), а высота разная (высота Прям.1
fmax , а высота Прям.2 |
fmin ). |
Если |
fmax ≤ 0, |
S+ |
=0, |
значит, функция внизу; |
если |
fmin |
³ 0 , S− = |
0, |
то |
функция вверху. Поэтому, чтобы найти интеграл одномерной функции, нужно найти максим. и миним.
значения функции на этом отрезке, проверить fmax ≤ 0
или fmin ³ 0 . Интеграл равен S+ - S− . Для того чтобы определить, что точка попадает в положительную область
yi |
≤ |
f (xi ) , |
при |
этом |
yi ³ 0, yi Î [0; fmax ] |
и |
yi |
³ |
f (xi ) |
, при этом |
yi ≤ |
0, yi [0; fmin ] ,\. |
|
3) Методы случайного поиска Поиск – задача определения максимума или минимума
функции, она сложная для многомерного случая. Если нет дополнительных условий-ограничений, то можно использовать методы градиентного поиска и метод координатной релаксации. Но существует возможность использовать и метод Монте-Карло:
Пусть задана некая область S в системе координат. В этой
области есть одна точка экстремума (максимума или минимума). Нужно найти эту точку. Для метода МонтеКарло сгенерируем две последовательнсти: n, сгенерируем
42

xi |
= |
xmax + |
|
(xmax − |
xmin )ξ i |
, |
|
|
|
|
|
|||||||||||||
yi |
= |
ymax + |
( ymax − ymin )η i |
|
|
|
|
|
|
|
|
|
и |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
, |
|
|
|
ξ |
i |
[ |
] |
|||||||||||||||||
|
|
|
|
|
|
|
|
0;1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
η i [0;1] |
|
|
|
ymax |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
, |
xmax |
, |
|
xmin |
|
|
|
|||||||||||
, где |
|
, |
ymin |
- |
границы |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
. Тогда |
( xi ; yi ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
области |
|
S |
|
точки |
|
|
лежат |
|
в |
области. |
||||||||||||||
Вычислим в |
|
|
|
|
|
|
|
функций |
||||||||||||||||
|
этих |
точках значения |
|
|
||||||||||||||||||||
fi = f (xi ; yi ) . Затем среди этих значений найдем
максимальное/минимальное. По теории вероятности следует, что если количество опытов устремить в бесконечность, то это экстремальное значение стремится к искомому значению. Тогда существуют следующие
варианты:
а) простой поиск, берем побольше точек и считаем, что максимальное значение соответствует нашему максимальному значению; б) поиск с аккомодацией – проводим несколько
экспериментов, но каждый раз область уменьшаем так, чтобы максимальное значение было в центре. При этом центр области выбирается в текущем максимальном значении. Очевидно, что этот метод более быстрый и требует меньше случайных точек, так как при этом уменьшается область, их плотность увеличивается.
43
в) метод последовательного поиска – точки с самого начала берутся в маленьком окошке, но это окошко перемещается так от шага к шагу, чтобы максимальное значение было в центре.
Так как во 2 и 3 случаях повторять процесс можно до бесконечности, то мы остановимся тогда, когда размер области или расстояние перемещения для центра окна меньше заданной погрешности. Существуют так же варианты, которые совмещают в себе 2-й и 3-й подходы.
В статистич. моделировании принято использовать случайные числа, кот-е наз генераторами. Обычно используют генератор случ чисел равномерно распределенных на диапазоне от 0 до 1. Имея такой генератор можно строить все другие последовательности. Распределение наз равномерным если вероятность появления на любом из отрезков равновероятна. Вероятность на отрезке прямопропорциональна длине отрезка.
Псевдослучайные числа отличаются от случайных тем, что они не случайные, но очень похожи на случайные, фактически они генерируются по формуле:.
xi+1 = f (xi, xi-1,…)
Псевдослучайная последовательность всё время одна и та же, повторяется, её менять можно только меняя точку входа.Как правило, в псевдослучайной последовательности существует период Т, т.е. через период элемент повторяется: xi+Т = xi. Этот период должен быть больше чем длина последовательности. Последействие выражается в том, что есть корреляция между элементами. Корреляция – это зависимость между двумя последовательностями случайных чисел, определяется коэффициентом корреляции.Для построения генератора равномерно распределенной пос-ти дейст-х чисел от 0 до 1 исполь. следующие методы:
44
1)аппаратный, в этом мет-е генер-р предст-т из себя отдельный прибор, в кот-м есть источник шума, теплового, квантового или радиоактив-го. Тепловой шум может создавать радиоакт. лампа или полупроводниковый прибор. Однако данный вариант не очень надежен, т.к. накладные шумы от внешней температуры. Источник квантового шума-это туннельный диод . Это самый дешевый способ, есть проблема надежности из-за влияния окружающей среды. Радиоакти-й источник надежно, но дорого. Аппарат создает эл. эмпульсы величина или расстояние м/д кот-ми меняется случ. образом. Далее спец. схема оцифровки превращает этот сигнал в после-ть чисел.
2)табличный, кем-то спец-м образом сгенерированы десятки-тысяч чисел, к-рые проверены и помещены в спец. таблицу, таб. расположена в файле, оттуда мы можем брать начиная с любого места нужную нам пос-ть чисел. Здесь
одна проблема таб. должна быть большой. |
|
|
3)алгоритмический, исполь-ся итерац-я |
фор-ла |
вида |
xin = f (xi , xi − 1,...) по кот-ой выч-ся |
эл-ты |
пос-ти |
псевдослучайных чисел. Псевдослуч-ое число похоже на слу-ое, но опреде-ся всетаки детерминированным процессом т.е. итерац. фор-ой. Изуч-е псевдослуч. чисел показывает, что по сравнению с случ числами у них есть след. недостатки: а)каждый раз генерир-ся одна и таже пость;б) в этой пос-ти есть период Т, такой , что xi + T = xi ; в)в пости есть последействия, т.е. текущий эл-т зависит от предшествующих, хотя для настоящих случ. чисел такой пос-ти не должно быть. Последействие опред-ся спец фуней корреляцией, к-ая опред-т зависим-ть м/д величинами. В тоже время алгоритмический генер. обладает большими достоинстваминет необ-ти покупать спец. прибор, можно всегда сгенирировать столько чисел сколько нужно не занимая места на диске, поэтому ученые стали стали
45
изучать различные генер-ы пытаясь сделать так, чтобы период был очень большим, последействие очень мало, а первая проблема снималась тем, что точка входа в итерац-
ю посл-ть постоянно меняется, т.е.меняется x0 .
Генератор Фон-Неймана. Исторически одним из1-ых был предложен Ф- Ней., но использовал метод середины квадрата. Пусть x0 начальное целое число, ко-ое состоит из 5 цифр. Тогда квадрат этого числа будет содержать 10 цифр, тогда возьмем из середины этого числа 5 цифр. Эти 5 цифр
дадут число x1 . В рез-те такого проц-са получ послед-ть
чисел, кот-ые похожи на случ-ые Þ их можно представить как дробную часть числа распределенную от0 до 1. Однако изуч. этой посл-ти показало, что в ней возник-т проц-ы вырождения. Обычно число приходит к 0 или 1. Поэтому этот мет-д не получил большого распространения.
Линейный конгруэнтный метод. Он сущ. в 2-х вариантах
виде |
смешанного |
|
генератора |
(Леммера) |
xi + 1 = |
(axi + C) mod M |
и мультипликативного |
||
xi + 1 = |
(axi ) mod M . |
Мультипликативный–частный |
||
случай смешанного при с=0. Было док-но, что период такого генератора яв-ся простым сомножителем числа М Þ что М выгоднее выбирать простым числом, чтобы период был больше. Возникла проблема найти такие большие простые числа. Очень удачным оказалось число Мерсонаэто наибольшее простое число, к-ое могло быть записано в 32-х разрядах ЭВМ, т.к. долгое время компью-ы были 32-х разрядными. То число Мерсона стало стандартным 231 − 1 . Кроме числа Мерсона матем-ки исследовали посл-ть при различных значениях а и с , были найдены оптимальные значения а и с.
46
Сдвиговый генератор Таусворта. Выпол. выч-я в таб. приходится не с 10-ми числами, а с двоичными. Поэтому Таусворд предложил модификацию генератора Леммера с учетом двоичных вычислений. На каждом шаге приходится умножать и делить целые числа, что довольно сложно в двоичной системе. Поэтому он предложил заменить эти операции на двоичное умножение и взятие двоичного остатка. Вместо больших чисел в его итерац-х числах получили разряды двоичных чисел 0 или 1. Если брать вместо числа М число 2, то фактическое значение последнего разряда произведения, определяется умножением последних разрядов произведения. Т.о. в методе Таусворда мы фактически вычисляем только 1
разряд |
по |
предыдущему |
|
разряду. |
xk |
= (C1 xk −1 + C2 xk −2 |
+ ... |
в рез- |
|
+ Cn xk −n ) mod 2 |
|
|||
|
|
|||
те действия генератора Таусворда формируется длинная пос-ть 1 и 0. Наилучший период T ≈ 2n − 1 , n –число
разрядов числа С. Далее из этой пос-ти 1 и 0 можно нарезать разных чисел. Данные генераторы были использованы с помощью следующих тестов: 1) тест на равномерность распределения; 2) тест на последействие, использовалась корреляция; 3) выборочный тест; 4) определение периода. Для того, чтобы улучшить качества генератора были созданы спец. методы улучшения кач-ва: метод возмущений и модификация с использованием разных последовательностей.
47
Экспоненциальное. F(x) = |
x |
ρ (t)dt . Пусть у нас есть |
||||||
ò |
|
|||||||
|
|
|
|
|
− ∞ |
|
|
|
случ. величина |
ξ [0;1] - |
равномерно |
распределена. |
|||||
Fξ (x) = P(η < x) òx ρ |
η (t)dt = Fη (x) |
|
||||||
|
|
|
− ∞ |
|
|
|
|
|
ρ |
η |
= λ e− λ t |
F = |
x λ e− λ t dt = - e− λ t |x |
= - e− λ x + 1 |
|||
|
|
η |
ò |
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
− λ x = ln(− F + 1) |
x = − |
1 |
ln(− F + 1) |
|
||||
|
|
|||||||
|
|
|
η |
|
λ |
η |
|
|
|
|
|
|
|
|
|
||
ρ ξ = 1
x
F(x) = 0ò ρ ξ (t)dt = x - 0 = x
xξ |
= |
Fξ , |
η |
= |
|
ξ |
) |
|
|
|
|
|
|
x |
= |
x |
|
|
|
|
g( |
. Мы |
должны |
η |
|
ξ |
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
g( |
) |
|
|
|
1 |
|
|
|
|
|
|
|
|
чтобы найти |
|
ξ |
|
η |
|
= - |
ln(ξ + |
1) . Т.о.чтобы |
|||||||||
|
|
|
λ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получить |
ρ η |
= |
λ e− λ t |
мы |
|
должны |
все |
значения |
ξ |
|
|||||||
преобразовать |
в |
|
η . |
Т.о. |
можно |
получить |
любое |
||||||||||
распределение. Если мы можем найти в явном виде его фун-ю распределения. В данном примере мы получили фор-лу с помощью которой можно получить по равномерному распределению экспоненциальное расп-е,
48
т.е. если xi распределено равномерно на [0;1], то |
|
|
yi |
будут |
||||||||||||
распределяться по экспо-у закону |
yi |
= − |
|
1 |
|
ln (1− |
xi ) . |
|||||||||
|
λ |
|||||||||||||||
|
|
|
|
|
|
|
|
|
[0;∞ |
) |
|
|
|
|||
Нормальное. |
|
− |
(x− x)2 |
, |
A = |
|
|
1 |
|
|
. |
Взять |
||||
ρ (x) = |
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2π σ |
|||||||||||
|
Ae |
2σ |
|
|
|
|
|
|
|
|
|
|
|
|||
первообразную от этой фун-и нельзя, но можно воспользося методом сложения посл-ти. Пусть мы с помощью генератора генерируем не 1 пос-ть, а несколько
xi\ , xi\ \ , xi\ \ \ ,... |
|
строим |
сумму. |
|||
|
x| |
+ x|| + x||| + ... |
|
|
||
yi = |
i |
i |
i |
|
, где N-число посл- |
|
|
|
|
|
|||
тей. В соответствии с центр. Теоремой теоремой вероятности, чем больше будет таких пос-тей, тем ближе
распред-е yi будет ближе к нормальному. Для получения
нормального распределения нужно 5 раз сгенерировать равномерно распределенные пос-ти. Затем сложить м/д собой эти пос-ти и найти их среднее.
Произвольное. Метод дистограмм наиболее трудоемкий, но зато позволяет построить любое расп-е, кот-ое задано графиком плотности. Разделим отрезок [a; b] на n равных
частей длиной h = |
|
a − |
b |
. В концах отрезка восстановим |
||||
|
n |
|
||||||
|
|
|
|
|
|
|
|
|
значение |
фун-и, |
это |
будут узлы. |
yi [ai ,bi ] , |
||||
R = ρ (y |
i |
) -высота |
столбика. |
|||||
i |
|
|
|
|
|
|
|
|
49
R = å |
Ri Þ α i = |
Ri |
-относительная |
высота. |
|
R |
|||||
i |
|
|
|
||
å α i |
= 1 Высота |
прямоугольников Ri д.б. |
|||
пропорциональна отрезку [ai ;bi ] . α i |
-вероятность, что |
||||
y [ai ,bi ] отсюда и идея метода дистограмм. Если мы
будем распределять случ.числа по этим отрезкам так, чтобы внутри отрезка вер-ть была равномерна, а м/д
отрезками опред-сь бы вероя-тью α i . Чем больше будет
этих отрезков, тем больше фун-я будет похожа на заданную, т.е. лучше будет аппроксимация.На каждом
отрезке |
|
распределение |
равномерное |
||
y |
i |
= |
a |
+ hx , x [0;1] |
нужно эти отрезки |
|
|
i |
i i |
|
|
переводить по очереди. Отсюда 1-ый вариант послед-но прямоуг-к за прямоуг-ом генерирует эти числа. Возникает проблема, что вер-ть попадания в каждый прямоуг-к разная зависит от высоты Þ кол-во точек которое попадает в каждый прямоуг-к разное и пропорциональное
α i . Мы могли бы опред-ть кол-во точек для каждого
отрезка, если бы знали общее кол-во точек, которое нам потребо-сь, но это известно не всегда. Поэтому предлаг-ся другой способ распределение чисел равномерно. Возьмем отрезок [0;1] разобьем на n частей, но не равных а
пропорциональных α i |
. å α i = 1 Тогда на [0;1] |
50
будут |
отрезки |
[Sk − 1, Sk ],Sk = |
åk α i |
||
|
|
|
|
|
i= 1 |
Sk = Sk − 1 + α |
k , S0 = |
0 |
Þ пусть |
мы |
|
|
|
||||
генерируем случ числа xi равномерно распределенные. Тогда вер-ть того, что xi попаджет на к отрезок будет равна длине этого отрезка α k . Мы получили следующие
yi |
преобразования по |
формуле |
y |
i |
= |
a |
k |
+ hx |
тогда |
||||
|
|
|
|
|
i |
||||||||
y |
k |
[a |
k |
;b ] |
причем вероя-ть |
|
попадания в |
этот |
|||||
|
|
k |
|
|
|
|
|
|
|
|
|
||
отрезок |
равна |
α k . |
Значит, что |
мы |
построили |
||||||||
распределение для |
yi виде дистограмм. |
|
|
|
|
||||||||
51

35.Моделирование потоков случайных событий. Сисмы массового обслуживания. Основные понятия и харки потоков. Класс-ция с-м масс.обс-ния. Оценка осн. Парпметров сис-м обс-ния(очередь, время ожидания)Формула Литтла.
Поток событий- последова-ть случ. событий, следующих одно за друг, в какие-то случ. моменты времени. Напр. поток вызовов на телефонной станции, поток ж.д.составов, поступающих на сортировочную станцию. Поток событ. можно наглядно изобразить рядом точек на оси времени Ot, положение кажд. из них случайно. Событ., образующие поток, сами по себе вероят-ми не обладают; вер-тями облад. др., производные от них события. В реальности события и заявки могут быть 2 видов:
1)однородные–это те заявки, которые всегда одинаковые по виду обслуживания.
2)неоднородные – обслуживаются по разному. При этом
заявки в потоке считаются неодновременными и практически мгновенными. Поток, в кот. не могут быть двух заявок одновременно, назыв. одинарным. Между событиями есть промежутки времени. Если эти промежутки времени строго фиксированы, то такой поток называется регулярным. Если время между событиями меняется случайно, то такой поток называется случайным. Доказано, что любой неоднородный поток может стать однородным, если его время обслуживания соединять с промежутками между событиями. Стационарный поток – это случайный поток, характеристика которого не меняется со временем. Под характеристикой понимается плотность потока λ, которая равна среднему количеству заявок, проходящих за ед. времени. Одинарный поток назыв. ещё простейшим
потоком. Интенсивность потока ( λ )-сред. число
52
событий, приходящееся на ед. времени. Интенс-ть может быть постоянной и зависящей от времени t.
Регулярный поток-когда соб. следуют одно за другим ч/з определенные равные промежутки времени.
Ещё одна характеристика: распределение определяет вероятность того, что событие произойдёт в какой-то промежуток времени.
Пуассоновский поток – это поток без последействия, т.е. вероятность появления события не зависит от предшествующих событий. Этот поток является наиболее случайным из всех возможных. Стационарный пуассоновский поток имеет следующее распределение (которое называется распределением пуасона):Pm(τ)=(λτ)m/m!*e-λτ, где λ – плотность потока; τ – промежуток времени;m – кол-во событий
Если пуассон-ий поток не стационарен,то P0(τ,t0)=am/m!
*e-a.
Функция λ(t) – это функция, которая показывает зав-сть плотности потока от времени для нестационарного режима.В любой фиксированный момент λ(tф)= λф – мгновенная плотность. Совершенно случайным потоком явл. только пуассоновский. Потоки с другим распределением можно представить как сумму случ. и детерминированных потоков. Причём случайная составляющая может представляться как сумма нескольких пуассоновских потоков с различным λ. → пуассоновские потоки должны иметь последействие, т.е. вероятность появления нового события от предшествующих событий.
Поток Пальма – это пуассоновский поток, в кот. на последействие наложены ограничения.Обычно потоки Пальма образуются с пом. потоков Эрланга (они наз. ещё
рекуррентными).Потоки Эрланга можно получить из пуассоновских потоков путём просеивания. Если из потока
53
выбирать каждую вторую заявку, то это поток Эрланга второго порядка, каждую третью – третьего и т.д.Док-но, что чем > порядок потока Эрланга, тем > последействие. При n→∞ получим регулярный поток. Тогда пуассоновский поток это поток Эрланга 1-го порядка. Следует учитывать, что для создания потоков Эрланга испся стационарные потоки. Поэтому стационарный пуассоновский поток называют простейшим.
СМО – это дискретные системы, которые могут быть как стахостические, так и детерминированные. Обычно это стахостические. Обычно СМО решается как имитационная модель. Началом теории СМО было решение задачи Эрланга: в 20-е годы ХХв. в Европе проходил процесс телефонизации. Эрланга телефонная компания попросила решить их проблему.Дано n-абонентов. Все они связаны с телефонной станцией. Проблема возникает, когда абоненты связываются с абонентами другой ТС. Между станциями существует m каналов, каждый канал – это дорогая вещь. Поэтому каналов < абонентов, т.е. m<n и возможна ситуация когда все каналы заняты, тогда абонент получает отказ (сбой) соединения. Фирма попросила определить оптимальное число каналов, чтобы с одной стороны их было поменьше (т.е. стоимость <), а качество соединения удовлетворяло заданным требованиям.
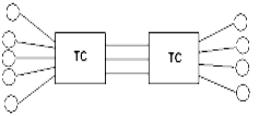 Т.е. может задаваться кол-во отказов до соединения, либо среднее время ожидания соединения. Эрланг провёл исследование реальной ТС, нашёл вероятности обслуживания абонентов, построил кривую потока заявок в соответствии с кот. была изменена тарифная система. Он определил основные характеристики такой системы обслуживания – это средняя пропускная
Т.е. может задаваться кол-во отказов до соединения, либо среднее время ожидания соединения. Эрланг провёл исследование реальной ТС, нашёл вероятности обслуживания абонентов, построил кривую потока заявок в соответствии с кот. была изменена тарифная система. Он определил основные характеристики такой системы обслуживания – это средняя пропускная
54
возможность канала, среднее время обслуживания и среднее количество отказов. Он получил систему ДУ для вероятности нахождения системы в каком-то состоянии. Аналогичную систему разработал Марков при изучении Марковских процессов. В дальнейшем оказалось, что системы типа СМО чрезвычайно распространены:А) торговля Б) транспорт В) многие технологические процессы и особенно работа персонала, т.к. человек всегда поступает довольно хаотично Г) элементы систем массового обслуживания были найдены в различных экономических системах Д) системы связи и коммуникации, компьютерные сети и сама ЭВМ.
СМО принято классифицировать двумя способами:
1.по типу потоков событий-заявок; 2. по дисциплине обслуживания.
Т.е. в общем случае СМО представляет из себя устройство для обслуживания, на которое поступает поток заявок. Устройство может обслужить заявку или сделать отказ.
Примеры СМО:
1.Ремонтная зона в автохозяйстве и автобусы, сошедшие с линии из-за поломки.
2.Травмопункт и больные, пришедшие на прием по случаю травмы
3.Телефонная станция с одним входом и абоненты, которых при занятом входе ставят в очередь.
СМО обозначают с помощью графосостояний:
 где 1,2,3 – это вершины, состояния; ребра – это переходы из одного состояния в
где 1,2,3 – это вершины, состояния; ребра – это переходы из одного состояния в
55

другое; λ - плотность потока; p - вероятности события. Можно для каждого состояния задать вер-ть того, что система нах-ся в каком-то состоянии. В теории массового обслуживания часто встречается схема гибели и размножения, если граф состояний системы представ. собой «схему гибели и размножения», то уравнение Колмогорова, алгебраич. ур-ия для финальных вероятностей для некоторых случаев удается решить заранее, в буквенном виде.
Уравнения Колмогорова-Эрланга:
dP
dt1 = λ 21 p2 + λ 31 p3 − p1 (λ 12 + λ 13 )
dP2 = λ |
12 |
p + λ |
32 |
p |
3 |
− p |
2 |
(λ |
21 |
+ λ |
23 |
) |
|
||
dt |
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dP3 |
|
= λ 23 p2 |
+ λ 13 p1 − |
p3 (λ 31 + λ 32 ) |
|
|
|
, |
где |
||||||
dt |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p1 + p2 + p3 = 1.
Причем входящий поток идет с «+», исходящий – с «–». Ур-я хар-ны для колебательной системы, в них есть переходные процессы, а затем система переходит к устойчивому, равновесному состоянию. марков и Колмогоров док-ли, что через опред-ое время устанавливается равновесное – финитное – состояние. Чтобы получить финитное состояние, необх-мо, чтобы все вер-ти =0:
dPdt1 = dPdt2 = dPdt3 = 0 . Тогда финитное решение ур-я Колмогорова-Эрланга:
56

dP1 |
= λ |
21 |
p |
2 |
+ λ |
31 |
p |
3 |
− p (λ |
12 |
+ λ |
13 |
) |
|
|||||||||||||
dt |
|
|
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
dPdt2 = λ 12 p1 + λ 32 p3 − p2 (λ 21 + λ 23 )
dP3 |
= λ |
23 |
p |
2 |
+ λ |
13 |
p − p |
3 |
(λ |
31 |
+ λ |
32 |
) |
|
|||||||||||||
dt |
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
p1 + p2 + |
|
p3 = 1 |
|
|
|
|
|
|
|||||
Решая эти уравнения можно определить характеристики
СМО:
1)средняя загруженность узлов обслуживания; 2)среднее время обслуживания заявки; 3)среднее время ожидания в очереди; 4)средняя длина очереди.
В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует.В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной. Эти СМО чаще встречаются на практике. Обслуживание с приоритетом- когда заявки обслуж-ся вне очереди.Абсолютный приоритет – когда заявка с более высоким приоритетом «вытесняет» из-под обслуживания заявку с низшим. Относительный приор.- когда начатое обслуживание доводится до конца, а заявка в более высоким приоритетом имеет лишь право на лучшее местов очереди. СМО с многофазовым обслуживанием – состоит из нескольких последовательных этапов или фаз. В открытой СМО характеристики потока заявок не зависят от того, в каком
57
состоянии сама СМО (ск-ко каналов занято). В замкнутой СМО – зависят.
Рассмотрим схему гибели-размножения (автор Эрланг). Здесь возможны только переходы между соседними состояниями. Граф представляет собой ленту:
 Составим
Составим
|
|
|
|
|
~ |
|
~ |
|
|
|
|
|
~ |
|
|
λ |
01 |
|
~ |
|
|
||
уравнения: λ 10 p1 - |
λ 01 p0 |
= |
0 |
Þ |
|
p1 |
= |
|
|
|
|
p0 |
(1) |
||||||||||
|
λ |
10 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
~ |
|
|
|
~ |
|
~ |
|
|
|
|
~ |
|
|
λ 12λ 01 |
~ |
|
|
||||||
λ 01 p0 |
|
+ λ |
21 p2 - (λ 10 |
+ λ 12 ) p1 = |
0 Þ |
p2 = |
|
|
|
|
|
|
p0 |
|
Т.о., |
||||||||
|
|
λ 21λ 10 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
||
последующее значение можно выразить через p0 . |
|
|
|||||||||||||||||||||
~ |
|
|
|
λ |
01 ~ |
|
|
|
|
|
|
|
~ |
|
|
|
|
λ 12λ 01 |
~ |
||||
p1 |
= |
|
|
|
|
p0 , |
|
|
|
|
|
|
|
p2 |
= |
|
|
|
|
|
|
p0 , |
|
|
|
λ |
10 |
|
|
|
|
|
|
|
|
|
λ 21λ 10 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
~ |
|
|
|
λ |
23λ 12 λ 01 |
~ |
~ |
|
|
∏k |
λ γ − 1γ |
~ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
γ = 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
p3 |
= |
|
|
|
|
p0 |
, pk = |
|
|
|
|
p0 |
|
|
|
|
|
|
|
|
|
||
|
λ |
32 λ 21λ 10 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
∏ λ γ γ − 1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
~ |
~ |
|
~ |
|
γ = 1 |
|
|
|
~ |
|
|
|
|
|
|
|
||
Так |
|
как |
+ |
2 + + |
|
|
= 1, |
Эта |
|||||||||||||||
|
|
p0 + |
p1 |
p |
pk |
||||||||||||||||||
формула позволяет рассчитать вероятность p0 , не решая
58
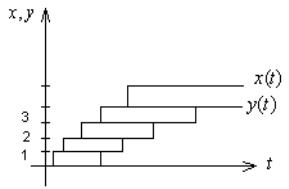
системы |
|
|
|
|
|
|
уравнений, |
|
|
k |
|
то |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
~ |
|
λ |
|
λ λ |
|
|
|
|
∏λγ −1γ |
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
||||||||
|
01 |
|
|
|
12 |
01 |
|
|
|
γ = |
|
|
|||||
p0 |
(1 + |
|
|
+ |
|
|
|
|
|
+ + |
|
|
|
|
) =1 |
||
λ10 |
λ21λ10 |
|
|
k |
|||||||||||||
|
|
|
|
|
|
∏λγ γ −1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
γ =1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
~ |
|
|
|
λ01 |
|
|
λ12 |
λ01 |
|
|
|
|
∏ λγ −1γ |
|
) . |
||
|
|
|
|
|
|
|
|
|
γ =1 |
|
|||||||
p0 |
= 1/(1 + |
|
|
|
+ |
|
|
|
|
+ |
+ |
|
|
|
|||
|
λ10 |
|
λ21λ10 |
k |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
∏ λγ γ −1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
γ =1
Формула Литтла
Подсчитаем среднее значение, которое касается СМО. Обозначим x(t) - число прибывающих заявок, y(t) - кот. обслужены (убывающие заявки). Разница между ними – это очередь. Рассмотрим график
Представим, что ввели функцию z(t) = x(t) − y(t) . T - промежуток времени, λ-
плотность потока. |
|
|
x(t)dt − |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
T z(t)dt = |
1 |
(T |
|
|
1 |
åi |
|
|
|
1 |
åi |
|
|
||
z |
ср |
= |
T |
Sпрям = |
t |
i |
= |
t |
λ |
||||||||||
|
|
|
|
||||||||||||||||
|
|
T |
ò0 |
T |
ò0 ò y(t)dt) = |
|
|
T |
|
|
Tλ |
i |
|
||||||
|
|
|
T |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
Графически этот интеграл равен сумме площадей прямоугольников.
N = T × λ - среднее количество заявок, которое прибывает за все время наблюдения
59
å ti |
- |
среднее |
время |
пребывания заявки в системе |
|
N |
|
|
|
|
|
å ti |
|
~ |
|
|
~ |
|
= |
t |
Þ |
zср = |
t × λ - формула Литтла, кот. |
N |
|
|
|
|
|
означает: среднее кол-во заявок в системе равно интенсивности потока, умноженного на среднее время пребывания заявки в системе.
Литтлу удалось док-ть, что эта формула справедлива:
1.при любом распределении потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания.
2.формула связывает среднее количество заявок в очереди с интенсивностью потока и среднем временем пребывания в очереди.
Таким образом, многие реальные СМО имеют точные решения или решения, полученные с помощью численных методов. И только наиболее сложные случаи требуют использования имитационного моделирования.
60
61
36.Основы теории погрешности. Прямая и обратная задача теории погрешности. Оценка погрешности. Понятие погрешности.
Погрешность – разница между точным значением величины и известным значением величины. Абсолютная погрешность – модуль этой разности. Известное значение называют приближённым. Погрешность возникает в случае неправильных исходных данных, в результате округления или упрощения математической задачи. Погрешность принято делить на три вида:
1)Неустранимая погрешность. Возникает из-за неточных исходных данных независимо от используемых методов и способов вычисления.
2)Погрешность метода – возникает из-за приближённого характера численных методов, которые используются при вычислениях (например, cosx и sinx ).
3)Вычислительная погрешность – это погрешность, связанная с ограниченным количеством разрядов ЭВМ.
Вычислительная ошибка всегда связанна с процедурой округления и само округление – попытка уменьшить вычислительную погрешность. Основная задача теории погрешности – оценить получаемую погрешность и предложить методы её уменьшения. Общая погрешность является суммой всех трёх видов погрешностей.
Опр 1. Абсолютной погрешностью приближенной величины A называется модуль разности приближённого и точного
значения величины: d = | A− Aт |
62

Опр 2. Относительной погрешностью γ |
называется |
отношение абсолютной погрешности к модулю приближённой
величины: γ = d( A)
| A|
Абсолютную погрешность практически невозможно определить, т.к. не известно точное значение. Поэтому пользуются оценками величины.
По определению обе погрешности положительны, а относительная погрешность 0 ≤ γ (A)≤ 1 .
Оценка погрешности.
По определению дано, что абсолютную погрешность найти никогда точно нельзя. Пользуются её оценками.
Опр 3. Оценка погрешности d называют положительную
величину |
~ |
, которая заблаговременно больше либо равна d : |
d |
~
d ³ d
По данному определению понятно что оценок бесконечно много.Среди всех возможных оценок есть наименьшая. Такая оценка называется предельной погрешностью. В некоторых случаях предельная погрешность равна абсолютной, а может быть и большей. Как правило, при вычислениях пользуются оценками погрешности не зная самой погрешности. Поэтому используют абсолютную погрешность.
Если известна абсолютная погрешность или какая-то её оценка, то можно утверждать что точное значение
принадлежит отрезку: Aт [ A− α ( A), A+ α (A)]
Данный отрезок принято называть интервалом неопределённости. Точное значение где-то в этом отрезке.
63

Для удобства его обозначают . Если число задано с погрешностью, то его цифры делятся на верные и приближённые. Все цифры, кот. по разряду больше погрешности назыв. верными, а остальные приближенными.Принято в абсолютной погрешности оставлять не более двух значащих цифр записи чисел записывают только одну приближённую цифру. В приближённом выражении производят округления таким образом, что бы приближённых цифр тоже осталось не более двух.
Существует также косвенная оценка погрешности – при итерационных вычислениях результатом является последовательность, которая сходится к искомому значению. Для оценки погрешности между пределом последовательности и очередным элементом пользуются
такой оценкой: limx → ∞ xn = x
x − xn ≤ xn + 1 − xn
Прямая и обратная задача теории погрешности.
Основной проблемой теории погрешности является поиск оценок. Выделяют прямую и обратную задачи теории погрешности.
1. Прямая задача: заданы приближённые величины А, B, C, D… и их абсолютные погрешности d(A),d(B),d(C) и функция F(A, B,C, D,...) . Требуется построить оценку погрешности функции d(F ) . Для решения прямой задачи
используется определение или метод разложения в ряд. Рассмотрим вариант определения.
64

А) Пусть дано A, B, F = A + B , d(A) , d(B) ; требуется найти d(F ) .
d (F )= F − Fт ; F = A + B; Fт = Aт + Bт .
Aт = A ± d (A), Bт = B ± d (B)
|
|
A+ B − A± d ( A) |
|
= |
||
|
|
|
||||
d(F ) |
|
− B ± d (B) |
|
|
||
|
± d ( A)± d (B) |
|
= |
|
|
|
= |
|
|
|
|
||
|
|
d ( A)+ d (B) |
|
|
|
|
|
|
|
|
|
||
С помощью определений абсолютной и относительной погрешности можно построить таблицу погрешностей при математических вычислениях.
d ( A + B) = | A+ B − ( A ± d ( A) + B ± d (B))|= = |± d ( A) ± d (B)|≤ d ( A) + d (B)
Абсолютная погрешность суммы равна сумме погрешностей.
d( A + B) = d( A) + d(B)
Для произведения F = A× B : d( A × B)
| A × B - (A± d( A)) * (B ± d(B)) |=
= |± A × d(B) ± B × d(B) ± d( A) × d(B) |£
£ | A|× d(B) + | B|× d( A) + d( A) × d(B) |
Для разности: d(A − B) = d( A) + d( A)
Следовательно, если производить вычитание близких величин, относительная погрешность может значительно возрастать.
65
γ (A− B) = |
|
d( A)+ |
d(B) |
Формула для оценки погрешности |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| A− |
B| |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
отношения |
|
|
F = |
|
|
A |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
æ |
|
A ö |
|
|
|
A A± d( A) |
|
|
|
|
|
|
AB± Ad(B) - AB± Bd( A) |
|
|
|
A |
|
d (B)+ |
|
B |
|
d ( A) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
ö |
|
|||||||||||||||||||
dç |
|
|
|
|
= |
|
|
- |
|
|
|
|
|
|
|
|
|
= = |
|
|
|
|
|
|
£ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
B± d(B) |
|
|
|
|
± Bd(B) |
|
|
B |
2 |
ç |
1- |
d (B) ÷ |
||||||||||||||||||||||||||||||
è |
|
B ø |
|
|
|
B |
|
|
|
|
|
|
|
|
B |
|
|
|
|
ç |
|
|
|
B |
|
÷ |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
A |
|
|
γ (B) + |
|
|
A |
|
|
γ ( |
A) |
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
ø |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
|
B |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1- γ (B) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
æ |
A ö |
|
|
γ ç |
|
÷ |
= |
|
|||
è |
B ø |
|
|
æ |
|
A ö |
|
|
|||||
dç |
|
|
|
|
÷ |
|
γ (B)+ γ (A) |
||
|
|
|
|
||||||
è |
|
B ø |
= |
||||||
|
|
|
A |
|
|
|
1- γ (B) |
||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
B |
|
|
|
|||
Б) Оценивание погрешности разложением в ряд Тейлора.
F(x + d ) = F(x) + F'(x)d
+ |
F''(x) |
d 2 + |
|
F'''(x) |
|
d 3 + ... |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
F(x + d ) = å∞ |
|
F ( k ) (x) |
d k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
k = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
F' |
|
|
|
|
|
|
|
|
± F''( A) |
|
|
|
|
|
|
|||||||||||
|
F( A ± d( A))= |
( A)± |
× |
, |
|
d( A) ± |
|
× d 2 ( A) ± .... |
|
|
|
||||||||||||||||||||||
|
|
2! |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
F( A ± d( A)) − F( A) |
|
|
|
= d(F( A)) |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
d(F( A)) £ |
|
|
F'( A) |
|
|
× d( A) + |
|
|
|
|
F''( A) |
|
|
|
× d 2 ( A) + ... = å∞ |
|
|
F k ( A) |
|
|
d k ( A) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1! |
|
|
|
|
|
2! |
|
|
|
|
|
|
k! |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 1 |
|
|
|
|
|||||||||||
66

Так как данная оценка бесконечна, то пользуются
последовательными |
приближениями. |
|
|
|
|
|
|
|
В |
|
|
первом |
||||||||||||||||||
приближении 1 –й элемент ряда: d(F ) = |
|
F' |
|
|
× d = |
|
|
dF1 , |
|
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
во |
втором |
соответственно |
|
|
|
|
|
|
второй |
- |
||||||||||||||||||||
|
d(F ) = |
|
|
F' |
|
× d + |
|
F''/ 2! |
|
× d 2 = dF2 |
в третьем – d(A)=dF2+ |
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
F''' |
|
|
× d 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
F ( n ) |
|
ö |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Формула для n - го приближения: |
dF = |
dF |
|
|
+ ç |
|
|
|
|
|
÷ × d n |
|
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
n |
n − 1 |
ç |
|
|
n! |
÷ |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
ø |
|
||||
Очевидно, что нужно вычислять приближения последовательно, сначала вычислив 1-ое, проверить достаточно ли точна погрешность, затем второе и т.д.
Для функций двух аргументов F(A,B) разложение будет гораздо, сложнее: dF≤(/sF/sA/)*d(A)+(/sF/sB/)*d(B)+(/s2F/sAsB/)*d2(A)+ (/s2F/sB2/)*d2(B), где s – частная производная
На практике (для таких функций) ограничиваются первым приближением.
Обратная задача: Заданы приближенные значения A,B,C,D, …; F(A,B,C,D,…); d(F)≤ε Найти при каких значениях d(А), d(B), d(C), d(D) достигается заданная погрешность функции. Для решения обратной задачи нужны дополнительные условия на погрешности, иначе задача имеет много решений. Если же наложить условия оптимальности то задача сводится к условной либо безусловной оптимизации. Существует несколько вариантов упрощённых величин:
А) Вариант равных вкладов. Предполагается, что в первом приближении каждая величина даёт равный вклад:
∂ F |
|
d( A) = |
|
∂ F |
|
|
d(B) = |
|
|
∂ F |
|
|
d(C) = ...= M |
|
|
|
|
|
|
||||||||||
∂ A |
∂ B |
∂ C |
||||||||||||
|
|
|
|
|
|
|
|
|||||||
67
Пусть всего
d(A)≤ |
|
d(F ) |
|
|
|
k |
|
∂ (F ) |
|
|
|
|
|
|
|||
|
|
|
|
||
|
|
∂ (A) |
|
|
|
величин K. Значит d(F )³ M × K и
(M – первое приближение).
Б) Метод равных погрешностей.
d( A) = d(B) = ...= d
|
|
¶ F |
|
æ |
|
¶ F |
|
|
|
¶ F |
|
ö |
d £ |
|
|
|
d(F ) |
|
||
d(F )³ d × å |
|
|
|
|
|
|
|
æ |
|
¶ (F) |
|
|
|
ö |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
ç |
|
|
+ |
|
|
÷ |
|
|
|
|
¶ F |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
¶ A |
|
= dç |
|
¶ A |
|
|
¶ B |
|
+ ...÷ |
|
ç |
|
|
+ |
+ ....÷ |
||||
|
|
|
|
|
|
|
|
¶ ( A) |
¶ B |
|||||||||||
|
|
i |
|
è |
|
|
|
|
|
|
|
ø |
|
ç |
|
|
|
÷ |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В) Задача условной оптимизации.
å d( Ai )→ min
Если использовать первое приближение и искать его минимум (min d1(F)) при различных значениях погрешности, то получится задача линейного программирования; если будем использовать второе и более высокие приближения, то нужно использовать задачу нелинейного программирования. На практике используют вариант равных вкладов и равных погрешностей на задаче линейного программирования.
68
69
37.Численные методы решения нелинейных уравнений с одним неизвестным.
Процесс решения нелинейных уравнений разбивается на два этапа: Отделение корней, Уточнение корней
Отделение корней нелинейного уравнения.
О1. Корень t |
отделен на отрезке [a;b] Df (a < b) , |
если t (a;b) |
и других корней в этом отрезке нет. При этом |
[a;b] называется отрезком изоляции корня t .
Отделить корни уравнения - значит для каждого из корней найти свои отрезки изоляции.
О2. Поиск приближенного значения корня с точностью до заданного достаточно малого числа ε > 0 называется
уточнением этого корня.
Следовательно, задача уточнения будет решена, если найдется
число x такое, что |
|
t − x |
|
≤ ε . Тогда |
t ≈ x с точностью до |
|
|
||||
ε . |
изоляции корня t |
|
|||
Если отрезок [a;b] |
найден, то любое число |
||||
из него можно взять в качестве приближенного корня.
Например, |
t ≈ |
a,t ≈ b,t ≈ |
|
(a + b) / 2 . |
Пусть |
h = |
b − a – |
|||||||||
длина отрезка. Поскольку |
|
t − |
a |
|
≤ |
h, |
|
t − |
b |
|
≤ h , концы отрезка |
|||||
|
|
|
|
|||||||||||||
являются |
приближениями |
|
к |
t |
|
|
с |
точностью |
до |
h . Легко |
||||||
проверить, |
что |
x имеет |
точность |
|
|
до h / 2 , |
т.е. |
обладает |
||||||||
лучшей характеристикой точности.
Чем меньше длина отрезка изоляции, тем выше точность приближения, однако с помощью используемых для отделения корней приемов получить отрезок достаточно малой длины трудно. Нужны специальные методы уточнения корней. Далее будет рассмотрено несколько таких методов, которые реализуют следующие два способа поиска
приближенного корня с заданной точностью ε > 0 :
70

1.Последовательно уменьшая длины отрезка изоляции корня по какому-либо правилу, отыскивается отрезок
[a;b] такой, что t [a;b] и b − a ≤ 2ε . Тогда приближенным корнем требуемой точности будет
середина отрезка [a;b] : x = |
(a + b) / 2 . |
||||||
2. Строится последовательность чисел |
x0 , x1 , , xn , , |
||||||
сходящаяся |
к корню |
t . |
Как |
только окажется |
|||
|
t − xn |
|
≤ ε , |
можно |
положить |
t ≈ xn . Такая |
|
|
|
||||||
последовательность называется последовательностью приближений, а определяющий её метод – методом последовательных приближений.
Первый способ удобен тем, что позволяет легко устанавливать завершение процесса уточнения, поскольку отрезки изоляции и их длины на каждом шаге вычислений известны.
Непосредственную проверку условия t − xn ≤ ε из второго
способа проводить не удается, ибо известен только корень t .
В то же время для каждого метода последовательных приближений есть возможность получить неравенства вида
t − xn |
|
≤ Vn (n = 1,2,...). |
(2) |
|
Здесь Vn – числовое выражение, значения которого при каждом n характеризуют степень близости приближения xn к корню, обеспечиваемую данным методом. Из (2)
следует, что за условие окончания процесса приближений можно взять неравенство: Vn ≤ ε .
71
Неравенство (2) позволяет решить и задачу определения абсолютной погрешности каждого приближения xn , ибо ясно, что (xn ) = Vn . .
Таким образом, отделить корни, значит задать такие отрезки, на которых корень существует и он единственный. Полученный отрезок будет интервалом неопределенности корня, а половина длины отрезка – оценкой абсолютной погрешности. Отделение корней обычно производится графически и (или) аналитически.
Графический способ отделения корней уравнения (1) заключается в поиске таких отрезков [a;b] D f , внутри которых находится абсцисса точки пересечения графика
функции y = f (x) с осью Ox , т.е. нуль функции f .
А) Графический метод.
Суть метода заключается в построении графика функции f(х) для нелинейного уравнения вида f(х)=0. На графике выделяются отрезки, на которых есть один единственный корень (точка пересечения функцией оси X). При необходимости выяснить поведение функции строится график части отрезка в увеличенном масштабе. Если в каком-то месте
функция асселирует |
(скачет) также нужно увеличить |
масштаб. |
|
Графический способ применяется наиболее часто. Обычно с него и начинают отделение корней, однако он не обладает большой точностью, и потому cделать окончательные выводы на его основе не всегда удается.
При схематическом изображении графиков можно ошибиться в выборе отрезка изоляции корня. Это случается, когда необходим отрезок небольшой длины или корни расположены близко. Здесь надо учесть, что последующие методы уточнения требуют от функций определенных свойств в окрестности корня. Чем мельче отрезок, тем вероятность
72
выполнения этих свойств выше. Бывает также, что на некоторых участках области определения уравнения графики функции располагаются настолько близко, что установить факт их пересечения или количество пересечений трудно.
Таким образом, результаты графического метода необходимо проверять и уточнять. Делается это аналитическими методами.
Б) Приближенный аналитический метод (проверка
изменения знака). |
|
Основа метода – теорема мат.анализа: |
|
Т1: (первая т. Больцано-Коши) Пусть функция f |
определена |
и непрерывна на отрезке [a;b] , причем на |
концах его |
принимает значения разных знаков, т.е. f (a) × f (b) < 0 .
Тогда существует по крайней мере одна точка t (a;b) , в которой значение функции равно нулю.
Т.е. если функция меняет знак на отрезке, то на этом отрезке она меняет корень.
Мы можем разбить весь отрезок на n частей, и проверить на каких частях функция меняет знак. Эти отрезки можно считать отрезками отделённых корней.
Приведем примерный алгоритм отделения корней уравнения f (x) = 0 аналитически:
1.Задается отрезок [а,b], на котором необходимо отделить корни функции f(х).
2.Задается начальное значение n и строится сетка хi =а+ih, h=(b-a)/n, i =0,1,2,...,n. Сетка делит отрезок на n частей с помощью n+1 точки.
3.Вычисляется значение функции f(хi)=fi, и вычисляется произведение значений функции на концах отрезка fi*fi+1, i =0,1,2,...,n+1.
4.Подсчитываем количество отрицательных произведений и запоминаем отрезки, где произведение отрицательно или равно 0. Число таких отрезков k. Каждый из таких отрезков должен содержать хотя бы 1 корень.
73
5. Увеличиваем n в два раза и повторяем процедуру. Получаем новое количество отрезков (корней) ki.
Если {k<k1 k=k1 и повторяем п.5 {k=k1 выход
Итерационные методы
Все итерационные методы можно считать частным случаем,
метода простой итерации.
Для метода простой итерации нелинейное уравнение вида F(x) = 0 необходимо превратить в уравнение явного вида
x = ϕ (x) . Такое превращение можно сделать следующим
способом:
ϕ ( x) = x ± kF( x)
Где k – любая положительная или отрицательная константа. Для нашего метода она выбирается из особого условия сходимости метода. Вычисления по итерационной формуле
x = ϕ ( x) начинают с x0 :
x1 = ϕ (x0 ) Þ x2 = ϕ (x1 ) Þ ..
.Þ xn = ϕ (xn − 1 )
x0 , x1 ,..., xn - итерационная последовательность.
Вычисления по итерационной формуле проводят в три основных этапа:
1. Определение начального приближения X 0 из условия сходимости.
2.Организация вычисления последовательности (итерационной или рекуррентной) по правилу.
3.Прерывание вычислений производится при достижении
косвенной оценки погрешности |xk-xk-1|<d.
Сходимость метода.
В общем случае сходимость итерационной последовательности зависит от ϕ и начального приближения
74
x0 . Она может сходиться и иметь предел или расходиться (не имея предела). Если предел -ет:
limn → ∞ xn = x
То он является решением нашей функции, а метод называется сходящимся. Опыт показывает, что возможен случай, когда метод сходится и расходится. С мат. точки зрения эта ситуация сходна с сжимающими отображениями. Если отображение сжимающее, то последовательность сходящаяся. Если условие сжимаемости не выполнено, то возможны два варианта:
1.через некоторое время элемент последовательности попадёт в зону сжимающегося отображения , и последовательность будет сходиться, но уже к другому корню.
2.последовательность уйдёт на ± бесконечность. В этом случае она ни когда не сойдется.
Если задана функция ϕ ( x) , то у корней может находиться некая область, где отображение сжимается, - это область сходимости. Если корень попал в такую область сходимости, то выбрав в качестве начального приближения любую точку этой области мы получим в пределе корень. Если выбрать вне этой области - не найдём. Если вокруг корня нет области, то получить его нельзя.
Функцию надо подбирать так чтобы вокруг нужного нам корня была область сходимости.
В итерационном методе хорд пользуются формулой
xn + 1 |
= xn − |
f ( xn )(xn − xn − 1 ) |
||
f ( xn ) − |
f (xn − 1 ) |
|||
|
|
|||
Чебышев предложил рассматривать не функцию f, а функцию обратную к ней: x = C( f )
75

xk = x + C1!' ( f ( xk ) − f ( x)) +
+ C2(!2) ( f ( xk ) − f ( x))2 + . .
Для k+1 –го элемента формула метода Чебышева:
xk + 1 = xk − |
F( xk ) |
− |
F"( xk )F 2 ( xk ) |
|
|
− |
|
||
F'( xk ) |
2(F'( xk ))3 |
|||
Если x – начальное приближение к корню, то элементы данного ряда дают последовательное приближение:
1- е приближение: |
|
xk = x + |
dc (− f ( x)) |
и т.д. В |
|
|
|
|
|
df |
|
рекуррентной форме получаем формулу Ньютона: |
|||||
x( k ) = x( k − 1) − |
f (x( k − 1) |
) |
|
|
|
f '(x( k − 1) ) |
|
|
|
||
Формула Ньютона соответствует методу касательных Ньютона. Фактически, производная функции определяет наклон касательной, т.е. в каждой точке мы берём касательную к заданной функции – метод касательных – предельный случай метода хорд.
Комбинированный метод
При исследовании данных методов была доказана следующая особенность: соответствующее приближение метода Ньютона и хорд дают значения, лежащие с разных сторон от корня. Поэтому создан комбинированный метод: каждое приближение в нём считается дважды (методом хорд и
76
методом Ньютона), а затем берётся среднее. Сходится комбинированный метод быстрее метода Ньютона.
Сравнение методов.
Сравнение методов показывает, что итерационные методы обычно вычисляют быстрее, зато они связаны с проверкой условия сходимости, что усложняют алгоритм.
Таким образом, если задача простая, то лучше использовать конечные методы или методы обратной интерполяции.
По скорости (быстроте сходимости) : 1. метод Чебышева 2. Комбинированный метод 3. Метод Ньютона 4. метод Хорд, 5. метод простой итерации, 6. метод дихотомии (хотя, подбирая формулу метода простой итерации можно добиться, чтобы он медленно сходился).
Особенность метода Чебышева в том, что можно построить формулу любого приближения:
1-е – метод Ньютона,
2-е – формула Чебышева и каждое новое приближение считается как уточнение предыдущего.
Уточнить корни можно вручную либо с помощью ЭВМ. Очевидно, что вручную лучше вычислять как можно меньше раз (сложные формулы). Значит, для ручных вычислений лучше использовать метод Чебышева, или обратную интерполяцию.
При расчетах на ЭВМ лучше использовать более простой и устойчивый метод: метод дихотомии, а для более сложных расчетов – метод Ньютона или комбинированный.
77

38.Реш-е СЛУ: точные методы Решение СЛУ: итерационные методы
ЧМ решения СЛУ
СЛУ запис-ся |
след образом ån aij x j |
= bi i = 1,2,.., n . |
|
j= 1 |
|
Коэф-ты aij |
образуют матрицу А |
сис-мы. Неиз-ные x j – |
вектор столбец неизвестных, В-вектор столбец правой части . В матричн. Форме СЛУ запис-ся след образом АХ=В. Иногда испол понят расширен матрицы сист, котор образ-ся путем
присоед-я вектора столбца справа и обозн A~ .Эл-ты aii образ-
ют главн диаг-ль матр, другие диаг-ли побочные. Для того, чтобы СУ имела 1 един реш-е необх, чтобы число урав было равно числу неизвестн; опред-ль матр А не равен 0.
L-матрицей наз матр, ниже главн диаг которой располож только 0. U-матр наз матр, выше главн диаг-ли которой располож только 0. L u U матр наз треугольными матр. Для численного реш-я СЛУ исп 2 типа методов - конечн и итерацион.
Конечн имеют строго определ кол-во операций.К ним относятся: М-д Гаусса, М-д полного исключения Жордано, Метод Халецкого. Кол-во операц в итерац методе завис от схти этого метода.
Метод Гаусса М-д Гаусса дел-ся на 2 этапа: прям и обратн ход. Прямой ход
– с помощ эквивал-х преобраз-ний, не изменяющих реш-е сист, производ-ся исключение эл-тов, лежащих выше или ниже главн диаг. Сущ 2 вар-та:1. приведение матр к L(ниже гл.диог.0) или U(наоборот) виду; 2.в общем случае получить треуг матр.
78
Обратн ход исп для опред-я неиз-х x j . В кач-ве эквив преобраз, не изменяющих реш-е сист явл следующее преоб-
ние матр A~ :
1.делен или умнож строки на постоян число, большее 0 2.слож или вычит 2 строк 3.постр-е лин-х комбинац строк 4.перест-ка строк
5. переест-ка столб-в с одноврем измен-м индексов перем-х Рассм процесс исключ прямого хода на примере получ-ия L- матр. Нужно исключ эл-ты, лежащ ниже главн диаг, при этом исключ-ем будет обращ-е в 0 этих эл-тов.Исключ-е произ-ся по столбцам, при этои базовым явл элемент главн диаг.
a |
/ |
|
= |
akj − amj |
akm |
/ |
|
|
|
akm |
|
kj |
|
b |
k |
= |
bk − bm |
|
|||
|
amm |
amm |
m=1,2,..,n-1 k=m+1,m+2,..,n j=m,m+1,..,n
А для U-матр выпол m=n,n-1…2 k=m-1,m-2,..,1 j=n,n-1,…,1
Точность выч-я по Гауссу опред-ся процессами округления в дан форме. Если диаг эл-т равен 0, то выч-ть нельзя, а если очень мал, то рез-т будет очень неточным. Сущ модификация м-да Гаусса за счет исп-я выбора главн эл-та. Главн эл-т – диаг эл-т, котор испол при вычисл.В процессе вычисл исп-ся все эл-ты главн диаг в кач-ве главн эл-тов, поэтому на главн диаг матр сист-мы желательно иметь макс по модулю эл-ты в своих столбцах или строках. Выбор такого эл-та может произся либо перест-кой строк расшир матр, либо перест-кой
79
столбцов. Во 2 случ необх переименовывать перем-ные. Чаще всего использ-ся 1 вар-т – переест-ка строк.
Т.о м-д Гаусса сущ 2 видов: просто м-д Гаусса и м-д Гаусса с выбором главн эл-та.
Расс обрат ход м-да Гаусса.Для L-матр:
xk |
= |
1 |
|
* |
|
|
¢ |
|
|
|
|||
|
|
akk |
|
|
||
æ |
¢ |
|
|
n |
¢ |
ö |
ç |
- å |
÷ |
||||
*ç |
bk |
akj x j ÷ |
||||
è |
|
|
j= k + 1 |
ø |
||
k=n,n-1,n-2,..,1. Для U-матр:
xk = |
|
|
1 |
|
* |
|
|
|
|
¢ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
akk |
|
|
ö k=1,2,.,n |
||
æ |
|
|
k− 1 |
|
|||
ç |
¢ |
|
å |
|
¢ |
÷ |
|
*ç bk - |
|
akj xj ÷ |
|||||
è |
|
|
j= 1 |
|
ø |
||
М-д полного исключения Жордано Жордан предложил исключ эл-ты не только выше, но и ниже
главн диаг. В рез-те матр станов-ся полностью диаг-ной, т.е. все эл-ты кроме диаг-х равны 0.Для этого исключ можно восп той же формой. Но циклы в м-де Жордано по иному m=1,2,..,n-1; k¹ m; j=1,..,n. Обратн ход в м-де Жордано прост
xi = |
bi′ |
, i=1,2,..,n |
|
′ |
|||
|
|
||
|
aii |
|
Штрих обозн, что это эл-ты расшир матр, преобразованные после процедуры исключения Замеч1.В принципе в м-де Жордано можно исп выбор главн
эл-та, но при этом сама процедура выбора очень сильно услож-ся, т.к. необх брать эл-ты как выше, так и ниже главн
80

диаг. 2. В м-де Гаусса 2 этапа-прямой и обратн ход. Прямой ход обычно требует больше операций, чем обратный. М-д Жордано не имеет прак-ки обрат хода, а сост из 2 прямых ходов. Далее рассм м-д Халецкого.В нем нет прямого хода, а 2 обратн, но при этом произ-ся предварит преобр-е исходн матр.
Метод Халецкого
М-д сост в разлож-и матр сист в произвед матр U и L, при этом эл-ты главн диаг lii=1. Сущ теорема алгебры, котор гласит, что для разлож произв матр А в произвед LU матриц необ и дост, чтобы все основн миноры были не равны 0. Для
вырожд матр это условие det A = 0 . Для невырожд матр
например a11 = 0 , но любую невырожд матр можно путем
перест-ки строк и столбцов привести к виду, в котором условие Сильвестра вып-ся, т.о перед разлож матр на LU нужно проверить ее на выпол-е условий сильвестра и при необ-ти произвести преобразование. Найдем формулы для опред-я эл-тов матр U и L. Выч-я будем производить последовательно по столбцам матр U и строкам матр L.
|
|
|
j− 1 |
|
uij |
= aij |
− å uik lkj -столбцы матр U. |
||
|
|
|
k = 1 |
|
|
|
|
i−1 |
|
lij |
= |
aij |
− å uik lkj -строки матр L. |
|
|
k =1 |
|||
|
|
|
||
|
|
|
uii |
|
Особ-ть выч-я по найденным формулам сост в том, что необх выч-ть послойно. Сначала столбец U, потом строку L. Нужно учит, что в формуле для U - i³ j, а для матр L- j³ i.
Алгоритм м-да Халецкого следующий:
1. проверяем условие для матр сист её разложимости в произвед LU
81

2. послойно находим эл-ты матр L и U 3.проводим обратный ход для выч-я yi 4. проводим обратный ход для выч-я xi
Потенциально м-д Халецкого имеет наим кол-во операций по сравнению с м-дом Гаусса иЖордано, но реализац-я дан м-да имеет более сложн алг-мы. В то же время дан м-д может сильно экономить ресурсы компьютера,т.к. после получ матр UL , их можно хранить вместе в одной матр.
Сравнивая эти м-ды можно сделать вывод:
1.м-д Гаусса наибол. экономн вар-т, если сист рещ-ся 1 раз. 2.м-д Жордано удобен,если матр сист имеет много 0, а также в случ одноврем-го реш-я большого кол-ва уравн с 1 матр и разными столбцами правой части.
3.м-д Халецкого также наиб удобен при реш-и большого колва уравн с одной матр сист.
ЧМ решения СЛУ
СЛУ запис-ся след образом |
ån aij x j = bi |
|
|
|
|
|
. |
||
|
|
i =1,2,.., n |
|||||||
|
|
|
j= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэф-ты aij |
|
|
|
||||||
образуют матрицу А |
сис-мы. Неиз-ные |
xj |
– |
||||||
вектор -столбец правой части В. В матричн. Форме СЛУ запис-ся
след образом АХ=В. Иногда испол понят расширен матрицы сист, котор образ-ся путем присоед-я вектора столбца справа
и обозн A~ .Эл-ты aii образ-ют главн диаг-ль матр, другие
диаг-ли побочные. Для того, чтобы СУ имела 1 един реш-е необх, чтобы число урав было равно числу неизвестн; опредль матр А не равен 0.
L-матрицей наз матр, ниже главн диаг которой располож только 0. U-матр наз матр, выше главн диаг-ли которой располож только 0. L u U матр наз треугольными матр. Для численного реш-я СЛУ исп 2 типа методов - конечн и
82

итерацион. Конечн имеют строго определ кол-во операций. Кол-во операц в итерац методе завис от сх-ти этого метода. Итерационные м-ды реш-я СЛАУ.
При наличии сист уравн мы можем оперировать с понят-ми матр и вектора. Реш-е–это вектор в некот n-мер- ном лин прост-ве. В алгебре для векторов вводят числовую хар-ку- норму. В некот случ она имеет аналогию с длиной и расст. Норма должна удовл:
1.||αx||=||α|| ||x|| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2.||x+y|| ≤ |
|
||x||+||y|| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
3.||x||=0 |
Þ |
|
x=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Обычно определяют 3 разных нормы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
n |
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.||x||1= |
|
å |
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
aij |
|
-первая норма |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= maxç |
å |
|
|
|
÷ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1≤ j≤ n è |
i=1 |
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
x |
|
|
|
|
|
|
= max( |
|
x |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
æ |
n |
aij |
|
ö |
- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= maxç |
å |
|
÷ |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i ç |
|
|
|
÷ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è j 1 |
ø |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бесконечная норма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å å aij2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
n |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3. |
|
x |
e = |
å |
u1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
e = |
|
|
|
|
|
i |
j |
|
|
-евклидова норма |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Нормы |
|
векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
и |
|
|
матр |
|
|
д.б. согласованы с помощью |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
Ax |
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
A |
= supç |
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
x |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
на итерац-х послед-х прибл-х, т.е. есть |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Итерац м-ды осн-ны |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
некая ф-ция, позвол наход k-ое прибл-е через (k-1) прибл-е |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x ( k ) |
|
|
|
|
= F ( x ( k −1) ) |
. х(0), х(1), х(2),.. сх- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ся к вектору х, если |
|
|
|
|
lim |
|
|
|
x − x ( k ) |
|
|
|
= 0 |
Т.к. оценить сх-ть |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
такой посл-ти невоз |
|
|
|
|
k → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
косвенной оценкой |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
-но, то польз-ся |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
погрешности, |
|
|
|
по |
которой |
|
|
|
|
x (k ) −x (k −1) |
|
|
|
|
<d |
|
- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
условие выхода или прекращ итерации. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
83

Метод простой итерации |
|
|
|
|
||||||||||||
Пусть задана СУ АХ=В, котор запис-ся |
ån |
aij x j = bi |
|
. Выразим |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
j= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
n |
|
в этой сист в кажд урав-нии по 1 перем |
|
|
′ |
, |
||||||||||||
|
xi = bi |
− å aij x j |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j= 1 |
|
где |
|
b′ |
= |
bi |
|
; |
|
|
|
|
|
|
|
|
||
|
aii |
|
|
|
|
|
|
|
|
|||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ì |
|
aij |
, j ¹ |
i |
|
|
|
|
|
|
|
|||
aij¢ |
= |
ï |
|
|
|
-это матр, на диаг которой |
распол |
0. У нас |
||||||||
|
aii |
|||||||||||||||
í |
|
|
|
|
|
|||||||||||
|
|
ï |
|
0, i = |
j |
|
|
|
|
|
|
|
||||
|
|
î |
|
|
|
|
|
|
|
|
||||||
получилось Х=В’-A’X, X(k)=B’-A’X(k-1)
В кач-ве нулевого прибл-я выбирают В’, т.е. Х(0)=В’. Сх-ть дан м-да, т.е. сущ-е предела посл-ти векторов док-ся теоремой.
Т: если матр сист А не вырожд и норма ||A’||<1, то дан м-д простой итерации будет сх-ся.
Замеч: т.о. сх-ть м-да прост итер-ии не завис от выбора нач приближ Х(0), а зависит только от матр сист. Усл-ем сх-ти будет след формула ||A’||<1.В кач-ве нормы м.б. выбрана любая из 3 норм. По 1 норме норма матр равна сумме модулей эл-тов столбца, котор имеет макс сумму. По бескон норме норма равна сумме модулей эл-тов строки, среди которых
|
|
|
|
|
|
|
ì |
max å |
|
aij |
|
< 1 |
|
|
|
|
|
|
|
|
|
|
|||||
выбир-ся макс. Т.о. получ. Что либо |
ï |
i |
j |
|
|
|
|
||||||
|
|
|
|
||||||||||
í |
max å |
|
aij¢ |
|
< 1 |
||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
ï |
|
|
||||
|
|
|
|
|
|
|
î |
j |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
maxi |
å |
|
aij |
|
< 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
aii |
|
|
|
|
|
|
|
||||||
|
j ¹ i |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
Для всех строк |
|
|
|
|
|
|
|
|
|||||
84

å aij < aii -условие диагон-го преобладания. Модуль
j ¹ i
эл-та главн диаг больше суммы модулей остальн эл-тов строки. Такое усл-е спр-во для всех строк.
å aij < aii i¹ j
В дан случ диаг эл-т д.б. больше по модулю суммы модулей остальных эл-тов столбца. Это св-во спр-во для всех столбцов. Если же норма =1, то сказать о сх-ти ничего нельзя. Алгоритм простой итерац:
1.выбир Х(0)=В’ и преобраз матр сист к итерац виду 2.используем итер фор-лу и наход следующ приближ 3.сраним по фор-ле
|
|
x (k ) −x (k −1) |
|
|
|
<d |
норму с |
|
|
|
|
||||
|
в противн |
||||||
задан погр-ю. Если усл-е выпол, то прекращ выч-е, |
|||||||
случ возвр-ся к пункту2. |
|
|
|
||||
Метод Зейделя |
|
|
|
||||
Зейдель предложил усов-ть итерац ф-лу путем исп-я уже получ-х элем-тов вектора Х, тогда
(k ) |
= |
′ − |
n |
′ |
(k −1) |
− |
|
− |
i- 1 |
′ ( k ) |
. Каждое |
xi |
|
bi |
å aij x j |
|
|
|
å |
aij x j |
|
||
|
|
|
j = i |
|
|
|
|
|
j= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
приближение сх-ся быстрее, чем у простой итерац, поэтому весь м-д сх-ся гораздо быстрее, кроме того в случае, когда м-д
прост итерац не сх-ся, м-д Зейделя иногда сх-ся. Метод координатной релаксации
Этот м-д заключ в следующем: после уточнения каждой коорд-ты по м-ду Зейделя, произв-ся смещение в том же направлении(смещение компонентов в одном и том же направл), на релаксационную часть этого смещения. Т.о. приближения отыскив-ся из соотнош
85

(B - D)xn+1 +
æ |
|
n+1 |
|
n ö |
n |
||
x |
+ px |
+Cx =b |
|||||
ç |
|
|
÷ |
||||
|
|
|
|
|
|||
Dç |
|
1+ p |
÷ |
|
|||
è |
|
ø |
|
||||
D-диагон матр с эл-ми aii по диаг-ли
При A>0 целесообразно брать показ-ль релаксации -1<p<1, в случае 0<p<1 м-д релаксации обычно наз м-дом сверхрелаксации. В частности, во многих случаях оптим-ной знач парам-ра релак-ции р опред-ся экспериментально. Иногда р зависит от n и i. Заключаем, что при
-1<p<1 всегда
F ( x n +1 ) <F ( x n ) |
n |
¹ X |
, где |
|
0 |
0 |
x |
|
|
F0(xn)- ф-ция, равная F(x)+(AX,X)==(A(x-X),x-X) Метод минимальных невязок
Для решения линейных систем уравнений можно применять и различные методы поиска экстремумов. Проблема решения системы уравнений заменяется эквивалентной задачей нахождения экстремума функции n переменных.
Одним из примеров является метод минимальных невязок. Вектор невязок определяется следующим образом.
Очевидно, что если на место вектора (Х) подставить вектор решения, то второе слагаемое окажется равным вектору свободных членов и вектор невязок становится нулевым.
Таким образом, минимизация компонентов вектора невязок эквивалентна задаче решения уравнений. Что бы знак невязок не влиял на результат, минимизируют сумму квадратов невязок (скалярное произведение вектора на себя):
86
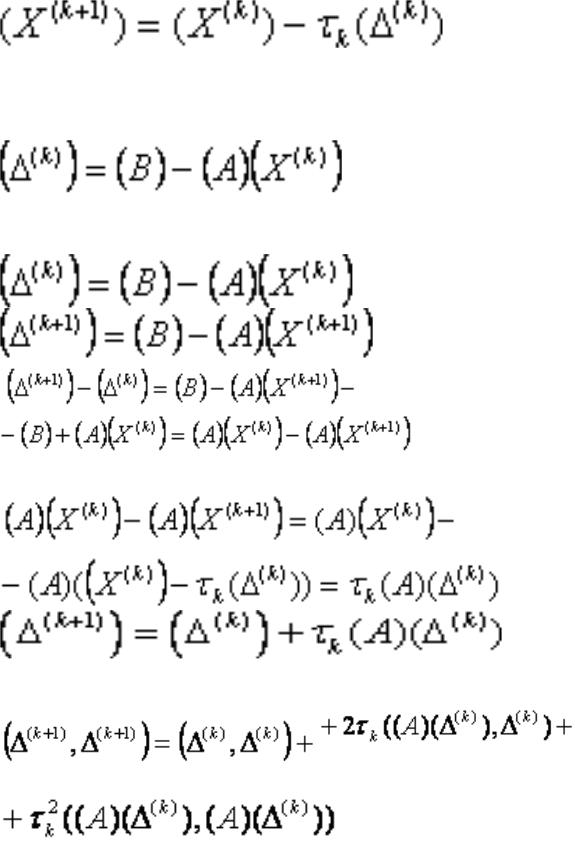
Запишем итерационную формулу поиска решения в следующем виде
где индекс k обозначает номер итерационного шага, тау – константа, которую нам необходимо определить, (k) (дельта)
– вектор невязок на этом шаге.
Рассмотрим разность векторов невязок на двух последовательных шагах k и k+1
после подстановки имеем
Скалярное произведение этого вектора на себя имеет вид
Параметр тау можно выбрать таким образом, чтобы левая часть была минимальной. Условием экстремума является равенство нулю производной по тау правой части выражения
87
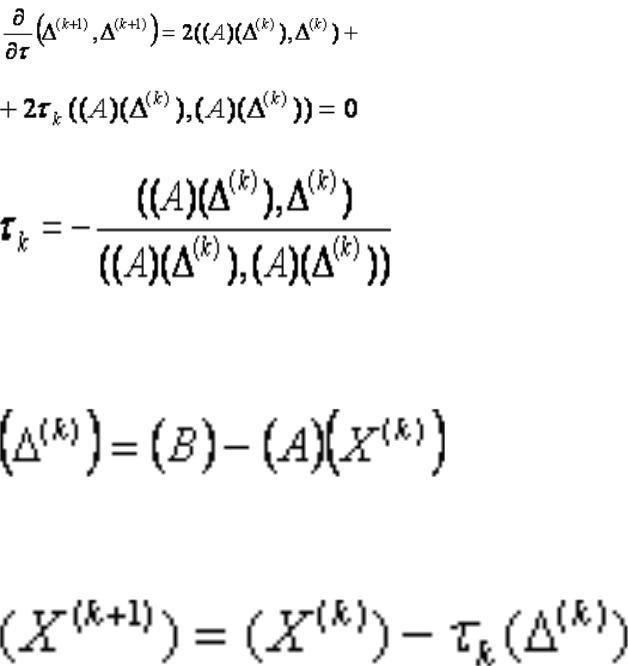
откуда,
Окончательно, k-ый шаг метода выглядит следующим образом:
1.Задается начальное приближение (Х(k))
2.Рассчитывается вектор невязок
3.Рассчитывается параметр тау. Для этого перемножается матрица коэффициентов и вектор невязок. Затем вычисляется его скалярный квадрат и произведение на матрицу невязок.
4.Рассчитывается новое приближение к вектору-решению
5.Проверяется один из критериев сходимости и, при необходимости, происходит переход к пункту 2.
88
89
39 Численная интерполяция: методы Лагранжа и Ньютона.
Понятие аппроксимации и интерполяции. Интерполяционные полиномы. Полином Лагранжа. Оценка погрешности интерполяции. Полином Ньютона. Разделенные разности. Сравнение полиномов Лагранжа и Ньютона.
Интерполяция и аппроксимация функций Аппроксимация – замена одной функции на другую,
удовлетворяющую условию близости. Условие близости – строгое математическое ограничение, которое позволяет в идеале выбрать единственную функцию. Функция, которую заменяют при аппроксимации принято называть аппроксимируемой. Функцию, которой заменяют аппроксимируемую принято называть аппроксимирующей. Смысл аппроксимации в том, чтобы более сложную или неявную аппроксимируемую функцию заменить более простой аппроксимирующей. Поэтому аппроксимирующие функции, как правило, элементарные – полиномы, тригонометрические функции и т.д.
Интерполяция – вид аппроксимации, для которого условие близости – совпадение значений функций в отдельных точках (узлах интерполяции). Пусть задан отрезок [a,b] на котором строится интерполирующая функция L(x) для интерполируемой F(x). Этот отрезок разбиваем на n частей точками xi = a+i*h –узлами интерполяции, где h = (b-a)/n. Это вариант равноотстоящих узлов. В общем случае узлы расположены произвольно, но при этом одна из точек совпадает с a, а другая с b. Пронумеруем точки так, чтобы они
распределились по возрастанию: а= х0 < х1 < х2 < … < хn = b. При этом необходимо, чтобы точки не совпадали между собой. В узлах интерполяции зададим значения интерполируемой функции yi = F(xi) . Значения индекса меняются i=0,1,2,…n-1. Таким образом, задаются 2 набора значений xi, yi , которые должны быть связаны условием
90
интерполяции (условием близости) L(xi) = yi . Практически это совпадение функций L(x) и F(x) в узлах интерполяции. Этот вариант осуществляется, например, при построении графика функции по точкам. Принято приближение функции F(x) интерполирующей L(x) на отрезке [a,b] называть собственно интерполяцией, а вне данного отрезка экстраполяцией. Погрешностью интерполяции называют величину d(x)=|L(x) -
F(x)| .
На графике видно, что в узлах интерполяции погрешность равна нулю. Между узлами интерполяции погрешность положительна и не равна нулю, а в областях экстраполяции быстро растет.
Существуют различные варианты интерполяции (полиномиальная, тригонометрическая, кусочно-сплайновая и др.), но наиболее употребительна интерполяция полиномами.
Полиномом называют функцию вида Pn (x) = ån ak xk . Здесь
k = 0
наивысшая степень n называется порядком полинома. Полином легко вычисляется (например, по схеме вычисления Горнера), дифференцируется и интегрируется. Ищем интерполирующую функцию в виде полинома Ln(x).
Запишем условие близости интерполяции:
Ln (xi ) = fi = |
ån |
ak xik - система уравнений первой |
|
k = 0 |
|
степени для величин |
ak , где полином выражен формулой |
|
Ln (x) = ån ak xk |
и |
ak -неизвестные коэффициенты, |
k= 0 |
|
|
91
которые необходимо |
определить, а |
xik - |
степени узлов |
|||
интерполяции (узлы заданы по условию). |
|
|
||||
Для |
ak |
получаем |
систему |
линейных |
уравнений |
|
ån |
cik ak |
= fi , n -степень полинома, |
cik |
= xik , где |
||
k= 0 |
|
|
|
|
|
|
a0 ,..., an − (n + 1) неизвестный коэффициент.
Полином Лагранжа
Лагранж предложил строить интерполяционный полином в следующем виде:
|
n |
|
|
(x − |
xj ) |
|
|||||
Ln(x) = |
å |
fk P |
|
xi - узлы интерполяции, x - |
|||||||
|
|
|
|
|
|
, где |
|||||
|
(x |
− |
x |
|
) |
||||||
|
k= 0 |
j¹ |
k |
|
k |
|
|
j |
|
|
|
исследуемая точка, |
fi |
- значение интерполируемой функции в |
|||||||||
узле i. |
Условие |
|
интерполяции |
для полинома Лагранжа |
|||||||
Ln (x j ) = |
f j . |
|
Полином |
Лагранжа удовлетворяет |
|||||||
условию интерполяции.
Полином Лагранжа по сравнению с каноническим полиномом имеет важное преимущество – он вычисляется прямым способом, без решения системы уравнений. Это значительно облегчает вычисления. Кроме того, существует специальная вычислительная схема Эйткена, которая позволяет вычислять значения полинома Лагранжа быстрым способом (похожим на схему Горнера):
L012…n(x) = [(x-x0)*L12…n(x) - (x-xn)*L012…n-1(x)]/[xn –x0]
Здесь L012…n – полином n порядка по всем узлам, L12…n - полином n-1 порядка по узлам от 1 до n-го, L012…n-1 - полином n-1 порядка по узлам от 0 до n-1. Таким образом, схема
расчета ведется по увеличению степени полинома.
92
