Рекуррентные соотношения.

Рекуррентным соотношением, рекуррентным уравнением или рекуррентной формулой называется соотношение вида , которое позволяет вычислять все члены последовательности , если заданы ее первые k членов.

Пример 1.

1. Формула задает арифметическую прогрессию.

2. Формула определяет геометрическую прогрессию.

3. Формула задает последовательность чисел Фибоначчи.

В случае, когда рекуррентное соотношение линейно и однородно, т. е. выполняется соотношение вида

(1)

(p=const), последовательность называется возвратной. Многочлен

(2)

называется характеристическим для возвратной последовательности . Корни многочлена называются характеристическими.

Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим уравнением.

Описание общего уравнения соотношения (1) имеет аналоги с описанием решения обыкновенного дифференциального уравнения с постоянными коэффициентами.

Теорема 1. 1. Пусть - корень характеристического многочлена (2). Тогда последовательность , где c – произвольная константа, удовлетворяет соотношению (1).

2. Если - простые корни характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид , где - произвольные константы.

3. Если - корень кратности характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид , где - произвольные константы.

Зная общее решение рекуррентного уравнения (1), по начальным условиям, можно найти неопределенные постоянные и те самым получить решение уравнения (1) с данными начальными условиями.

Пример 2. Найти последовательность , удовлетворяющую рекуррентному соотношению и начальным условиям .

Корням характеристического многочлена являются числа . Следовательно, по теореме 3.1. общее решение имеет вид . Используя начальные условия, получаем систему

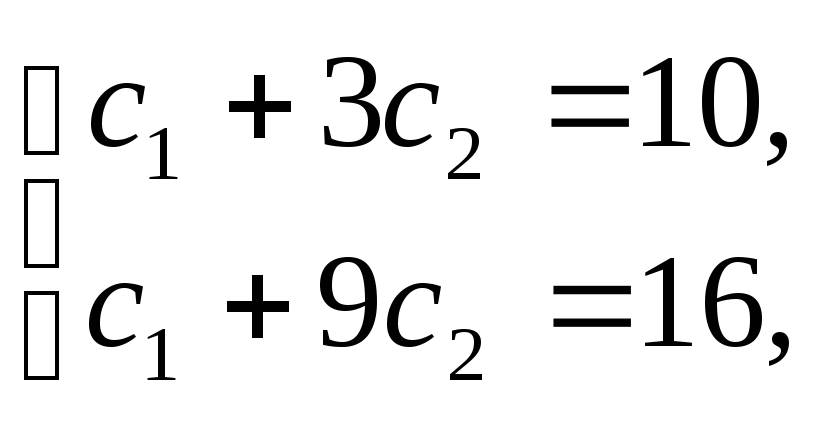
решая которую, находим и . Таким образом, .

Рассмотрим неоднородное линейное рекуррентное уравнение

(3)

Пусть - общее решение однородного уравнения (1), а - частное (конкретное) решение неоднородного уравнения (3). Тогда последовательность образует общее решение уравнения (3), и тем самым справедлива.

Теорема 2. Общее решение неоднородного линейного рекуррентного уравнения представляется в виде суммы общего решения соответствующего однородного линейного рекуррентного уравнения и некоторого частного решения неоднородного уравнения.

Таким образом, в силу теоремы 1. задача нахождения общего решения рекуррентного уравнения (3) сводится к нахождению некоторого частного решения.

В отдельных случаях имеются общие рецепты нахождения общего решения.

Если (где ) не является характеристическим корнем, то, подставляя в (3), получаем и отсюда , т. е. частное решение можно задать формулой .

Пусть - многочлен степени r от переменной n, и число 1 не является характеристическим корнем. Тогда и частное решение следует искать в виде . Подставляя многочлены в формулу (3), получаем

Сравнивая коэффициенты в левой и правой частях последнего равенства, получаем соотношения чисел , позволяющие эти числа определить.

Пример. Найти решение уравнения

(4)

с начальным условием .

Рассмотрим характеристический многочлен . Так как и правая часть уравнения (3) равна n+1, то частное решение будем искать в виде . Подставляя в уравнение (4), получаем . Приравнивая коэффициенты в левой и правой частях последнего равенства, получаем систему

откуда находим . Таким образом, частное решение уравнения (4) имеет вид . По теореме 3.1. общее решение однородного уравнения задается формулой , и по теореме 3.2. получаем общее решение уравнения (4): . Из начального условия находим , т. е. . Таким образом, .