- •Случайные события. Алгебра событий.
- •Классич определел вероятности. Основные св-ва вероятности.
- •Теор умнож вер. Независимые события.
- •Формула полной вероятности.
- •Биномиальное распределение.
- •Равномерное распредел вероятностей.Равномерный закон распределения.
- •Равномерное распредел на пл-ти.
- •В чем состоит схема расчета показателей эффективности одноканальной смо с ограниченной очередью?
Равномерное распредел на пл-ти.
Система
двух СВ называется равномерно
распределенной на плоскости,
если ее плотность вероятности f(x,
y)
= const
внутри некоторой области и равна 0 вне
ее. Пусть данная область-прямоугольник
вида![]() Тогда
из свойств f(x,
y)
следует,
Тогда
из свойств f(x,
y)
следует,
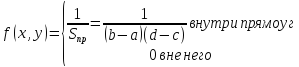
Найдем
двумерную функцию распределения:
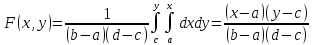 при
a
< x
< b,
c
< y
< d,
F(x,
y)
= 0 при x
≤ a
или
y
≤ c,
F(x,
y)
= 1 при x
≥ b,
y
≥ d.
Функции распредел составляющих, имеют
вид:
при
a
< x
< b,
c
< y
< d,
F(x,
y)
= 0 при x
≤ a
или
y
≤ c,
F(x,
y)
= 1 при x
≥ b,
y
≥ d.
Функции распредел составляющих, имеют
вид:
![]()
Условные
законы распределения составляющих
дискретной двумерной СВ. Условной
плотностью φ(х/у)
распределения
составляющих Х
при данном значении Y
= у
называется
![]()
Аналогично
определяется условная плотность
вероятности Y
при Х
= х:
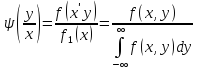
Линейная
регрессия.
Пусть составляющие Х
и Y
двумерной случайной величины (Х,
Y)
зависимы. Будем считать, что одну из них
можно приближенно представить как
линейную функцию другой, например Y
≈ g(Х)
=
α
+ βХ, и
определим параметры αи
β
с помощью метода наименьших квадратов.
Функция g(Х)
=
α
+ βХ
называется
наилучшим
приближением Y в
смысле метода наименьших квадратов,
если математическое ожидание М(Y
- g(Х))2
принимает наименьшее возможное значение;
функцию g(Х)
называют среднеквадратической
регрессией Yна
Х.
Теор.
Линейная
средняя квадратическая регрессия Yна
Х
имеет вид:
![]() где
где
![]()
![]() -коэфф
корреляции Х
иY.
Коэфф
-коэфф
корреляции Х
иY.
Коэфф![]() называется
коэфф
регрессии Y
на
Х,
а прямая
называется
коэфф
регрессии Y
на
Х,
а прямая 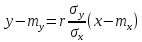 - прямой
среднеквадратич регрессии Y
на
Х.
Мин знач функции F(α,
β),
равно
- прямой
среднеквадратич регрессии Y
на
Х.
Мин знач функции F(α,
β),
равно![]() Эта
вел назыв остаточной
дисперсией
Y
относ Х
и характеризует величину ошибки,
допускаемой при замене Yна
g(Х)
=
α+βХ.
Прямая среднеквадратич регрессии Х
на Y:
Эта
вел назыв остаточной
дисперсией
Y
относ Х
и характеризует величину ошибки,
допускаемой при замене Yна
g(Х)
=
α+βХ.
Прямая среднеквадратич регрессии Х
на Y:![]()
Линейная корреляция. Для двумерной СВ (Х, Y) можно ввести так называемое условное мат ожид Yпри Х = х. Функцией регрессии Y на Х назыв условное мат ожид M( Y / x) = f(x). Аналогично определяется условное мат ожид Х и функция регрессии Х на Y. Если обе функции регрессии Х на Yи Y на Х линейны, то говорят, что Х и Yсвязаны линейной корреляционной зависимостью. Теор. Если двумерная случайная величина (Х, Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью.
Распределение
«хи-квадрат».
Пусть
имеется несколько нормированных
нормально распределенных случайных
величин: Х1,
Х2,…,
Хп
(ai
=
0, σi
=
1). Тогда сумма их квадратов
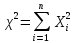 является
случайной величиной, распределенной
по так называемому закону
«хи-квадрат»
с k
= n
степенями
свободы; если же слагаемые связаны
каким-либо соотношением. Плотность
этого распределения
является
случайной величиной, распределенной
по так называемому закону
«хи-квадрат»
с k
= n
степенями
свободы; если же слагаемые связаны
каким-либо соотношением. Плотность
этого распределения
![]()
Здесь![]() -
гамма-функция. =>, распределение
«хи-квадрат» определяется одним
параметром – числом степеней свободы
k.
-
гамма-функция. =>, распределение
«хи-квадрат» определяется одним
параметром – числом степеней свободы
k.
Распределение
Стьюдента.
Рассмотрим
две независимые случайные величины: Z,
имеющую нормальное распределение и
нормированную, и
V,
распределенную по закону «хи-квадрат»
с
k
степенями свободы. Тогда величина
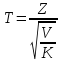 имеет
распределение, называемое t
– распределением или распределением
Стьюдента
с k
степенями свободы. С возрастанием числа
степеней свободы распределение Стьюдента
быстро приближается к нормальному.
имеет
распределение, называемое t
– распределением или распределением
Стьюдента
с k
степенями свободы. С возрастанием числа
степеней свободы распределение Стьюдента
быстро приближается к нормальному.
Распределение
Фишера. Рассмотрим
две независимые случайные величины Uи
V,
распределенные по закону «хи-квадрат»
со степенями свободы k1
и
k2
и образуем из них новую величину
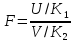 Ее
распределение называют распределением
F
Фишера со
степенями свободы k1
и k2.
Ее
распределение называют распределением
F
Фишера со
степенями свободы k1
и k2.
З-н больших чисел и неравенство Чебышева. Изуч статистических закономерностей позволило установить, что при некоторых условиях суммарное поведение большого кол-ва СВ почти утрачи-вает случайный характер и становится закономерным. В частности, если влияние на сумму отдельных слагаемых является равномерно малым, закон распределения суммы приближается к нормальному. Мат формулировка этого утверждения дается в группе теорем, называемой законом больших чисел. Неравенство Чебышева, используемое для доказательства дальнейших теорем, справедливо как для непрерывных, так и для дискретных СВ. Теор (нер-во Чебышева). p( | X – M(X)| < ε ) ≥ D(X) / ε².
Теоремы
Чебышева и Бернулли. теор
Чебышева. Если
Х1,
Х2,…,
Хп
– попарно независимые СВ, дисперсии
которых равномерно ограничены ( D(Xi)
≤ C),
то для сколь угодно малого числа ε
вероятность неравенства
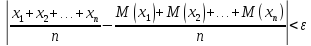 будет сколь угодно близка к 1, если число
случайных величин достаточно велико.
будет сколь угодно близка к 1, если число
случайных величин достаточно велико.
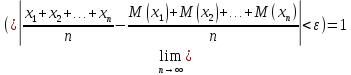 теор
Бернулли. Если
в каждом из п
независимых опытов вероятность р
появления события А
постоянна, то при достаточно большом
числе испытаний вероят-ность того, что
модуль отклонения относительной частоты
появлений А
в п
опытах от р
будет сколь угодно малым, как угодно
близка к 1:
теор
Бернулли. Если
в каждом из п
независимых опытов вероятность р
появления события А
постоянна, то при достаточно большом
числе испытаний вероят-ность того, что
модуль отклонения относительной частоты
появлений А
в п
опытах от р
будет сколь угодно малым, как угодно
близка к 1:
![]()
Характеристические
ф-ции, их св-ва. Характеристической
функцией
СВ Х
называется функция g(t)=M(eitX)
Таким образом,
g
(t)
представляет собой мат ожид некоторой
комплексной СВ U
= eitX,
связанной с величиной Х.
В частности, если Х
– дискретная СВ, заданная рядом
распределения, то
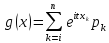 Для
непрерывной СВ с плотностью распределения
f(x)
Для
непрерывной СВ с плотностью распределения
f(x) Св-ва
характеристических функций. 1.
Функцию f(x)
можно найти по известной функции g(t)
по формуле
Св-ва
характеристических функций. 1.
Функцию f(x)
можно найти по известной функции g(t)
по формуле
 2. Если СВ Х
и Y
связаны соотношением Y
= aX,
то их характеристические функции связаны
соотношением gy
(t)
= gx
(at).
3. Характеристическая функция
суммы независимых СВ равна произведению
характеристических функций слагаемых:
для
2. Если СВ Х
и Y
связаны соотношением Y
= aX,
то их характеристические функции связаны
соотношением gy
(t)
= gx
(at).
3. Характеристическая функция
суммы независимых СВ равна произведению
характеристических функций слагаемых:
для
![]()
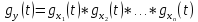
Центральная
предельная теорема для одинаково
распределенных слагаемых.
Теор.
Если Х1,
Х2,…,
Хп,…
- независимые СВ с одинаковым законом
распределения, мат ожид т
и дисперсией σ2,
то при неограниченном увеличении п
закон распределения суммы
![]() неограниченно
приближается к нормальному.
неограниченно
приближается к нормальному.
Теорема
Ляпунова. Теор.
Если СВ Х
представляет собой сумму очень большого
числа взаимно независимых СВ, для которых
выполнено условие:
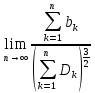 ,
где bk–
третий абсолютный центральный момент
величины Хк,
а Dk
– ее дисперсия, то Х
имеет распределение, близкое к нормальному.
,
где bk–
третий абсолютный центральный момент
величины Хк,
а Dk
– ее дисперсия, то Х
имеет распределение, близкое к нормальному.
Предельная
теорема Муавра-Лапласа. Теор.
Если
производится п
независимых опытов, в каждом из которых
событие А
появляется с вероятностью р,
то справедливо соотношение: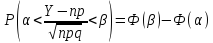 ,
где Y–
число появлений события А
в п
опытах, q
= 1 – p.
,
где Y–
число появлений события А
в п
опытах, q
= 1 – p.
Связь
распределений «хи-квадрат», Стьюдента
и Фишера с нормальным распределением.
Пусть
имеется несколько нормированных
нормально распределенных случайных
величин: Х1,
Х2,…,
Хп
(ai
=
0, σi
=
1). Тогда сумма их квадратов
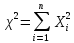 является
случайной величиной, распределенной
по так называемому закону
«хи-квадрат»
Следовательно, распределение «хи-квадрат»
определяется одним параметром – числом
степе-ней свободы k.
Распред.
Стьюдента.
Рассмотрим две независимые случайные
величины: Z,
имеющую нормальное распределение и
нормированную, и
V,
распределенную по закону «хи-квадрат»
с
k
степенями свободы. Тогда величина
является
случайной величиной, распределенной
по так называемому закону
«хи-квадрат»
Следовательно, распределение «хи-квадрат»
определяется одним параметром – числом
степе-ней свободы k.
Распред.
Стьюдента.
Рассмотрим две независимые случайные
величины: Z,
имеющую нормальное распределение и
нормированную, и
V,
распределенную по закону «хи-квадрат»
с
k
степенями свободы. Тогда величина
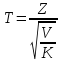 имеет
распределение, называемое t
– распределением или распределением
Стьюдента
с k
степенями свободы. С возрастанием числа
степеней свободы распределение Стьюдента
быстро приближается к нормальному.
Распред.
Фишера.
Рассмотрим две независимые случайные
величины Uи
V,
распределенные по закону «хи-квадрат»
со степенями свободы k1
и
k2
и образуем из них новую величину
имеет
распределение, называемое t
– распределением или распределением
Стьюдента
с k
степенями свободы. С возрастанием числа
степеней свободы распределение Стьюдента
быстро приближается к нормальному.
Распред.
Фишера.
Рассмотрим две независимые случайные
величины Uи
V,
распределенные по закону «хи-квадрат»
со степенями свободы k1
и
k2
и образуем из них новую величину
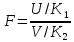 Ее
распределение называют распределением
F
Фишера со
степен свободы k1
и k2.
Ее
распределение называют распределением
F
Фишера со
степен свободы k1
и k2.
Начальные
и центральные моменты. Начальным
моментом порядка k
СВ
Х
называется мат ожид величины Xk:
νk
= M
(Xk).
В частности, ν1
= М(Х),
ν2
= М(Х2).=>,
дисперсия D(X)
= ν2
– ν1².
Центральным
моментом порядка k
СВ
Х
называется мат ожид величины (Х
– М(Х))k:
μk
= M((Х
– М(Х))k).
В частности, μ1
= M(Х
– М(Х))
= 0, μ2
= M((Х
– М(Х))2)
= D(X).
Можно получить соотношения, связывающие
начальные и центральные моменты:
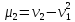 ,
,
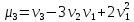 ,
,
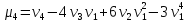
Мода, медиана, квантиль. Модой М дискретной СВ называется ее наиболее вероятное значение, модой М непрерывной СВ– значение, в котором плотность вероятности максимальна. З! 1. Если кривая распределения имеет больше одного максимума, распределение называется полимодальным, если эта кривая не имеет максимума, но имеет минимум – анти-модальным. Медианой Ме непрерывной СВ называют такое ее значение, для которого p( X < Me ) = p( X > Me ). Графически прямая х = Ме делит площадь фигуры, ограниченной кривой распределения, на две равные части. Для СВ Х с функцией распределения F(X) квантилью порядка р (0 < p < 1) называется число Кр такое, что F(Kp) ≤ p, F(Kp + 0) ≥ p. В частности, если F(X) строго монотонна, Кр: F(Kp) = p.
Коэф.
Ассиметрии и эксцесса.
Коэффициентом
асимметрии случайной
величины называется
![]()
![]() В частности, для
кривой, изображ на рис.1, Sk
> 0, а на
рис.2 - Sk
< 0. Эксцессом
СВ называется величина
В частности, для
кривой, изображ на рис.1, Sk
> 0, а на
рис.2 - Sk
< 0. Эксцессом
СВ называется величина

Числовые
характеристики двумерных СВ: нач и
цетральные моменты. Начальным
моментом порядка k,
s
двумерной
случайной величины (Х,
Y)
называется математическое ожидание
произведения Xk
на Ys:
αk,s
= M
(XkYs).
Для дискретных СВ![]() для
непрерывных СВ
для
непрерывных СВ
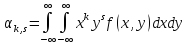 Центральным
моментом порядка k,
s
двумерной
СВ (Х,
Y)
называется мат ожид произведения (X
– M(X))k
на (Y
– M(Y))s:
μk,s
= M((X
– M(X))k(Y
– M(Y))s).
Для дискретных СВ
Центральным
моментом порядка k,
s
двумерной
СВ (Х,
Y)
называется мат ожид произведения (X
– M(X))k
на (Y
– M(Y))s:
μk,s
= M((X
– M(X))k(Y
– M(Y))s).
Для дискретных СВ
![]() для
непрерывных СВ
для
непрерывных СВ
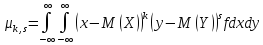 . При этом М(Х)
= α1,0,
M(Y)
= α0,1,
D(X)
= μ2,0,
D(Y)
= μ0,2.
. При этом М(Х)
= α1,0,
M(Y)
= α0,1,
D(X)
= μ2,0,
D(Y)
= μ0,2.
Корреляц
момент и коэф корреляции. Коррелированность
и зависимость СВ. Корреляционным
моментом системы
двух СВ называется второй смешанный
центральный момент:
Kxy
= μ1,1
= M((X
– M(X))(Y
– M(Y))).
Для
дискретных СВ
![]() для
непрерывных случайных величин
для
непрерывных случайных величин
![]() Безразмерной
характеристикой коррелированности
двух СВ является коэфф
корреляции
Безразмерной
характеристикой коррелированности
двух СВ является коэфф
корреляции
![]() Теор.
Теор.
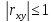
Ф-ции
от СВ. Ф-ции одного случ аргумента,
распред и мат ожид. Если
каждому возможному значению СВ Х
соответствует одно возможное значение
СВ Y,
то
Y
называют
функцией
случайного аргумента Х: Y=φ(X).
Выясним, как найти закон распред функции
по известному закону распред аргумента.
1) Пусть аргумент Х
– дискретная СВ, причем различным
значениям Х
соот-ветствуют различные значения Y.
Тогда вероятности соответствующих
значений Х
и Y
равны.
2) Если разным значениям Х
могут соответствовать одинаковые
значения Y,
то вероятности значений аргумента, при
которых функция принимает одно и то же
значение, складываются. Если Х
– непрерывная СВ, Y
= φ(X),
φ(x)
– монотонная и дифференцируемая функция,
а
ψ(у)
– функция, обратная к
φ(х),
то плотность распределения g(y)
случайно функции Y
равна: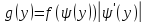 Мат
ожид функции одного случайного
аргумента.Пусть
Y
= φ(X)
– функция случайного аргумента Х,
и требуется найти еемат ожид, зная закон
распред Х.
1) Если Х
– дискретная СВ, то
Мат
ожид функции одного случайного
аргумента.Пусть
Y
= φ(X)
– функция случайного аргумента Х,
и требуется найти еемат ожид, зная закон
распред Х.
1) Если Х
– дискретная СВ, то![]() 2)
Если Х
– непрерывнаяСВ, то M(Y)
можно искать по-разному. Если известна
плотность распределения g(y),
то
2)
Если Х
– непрерывнаяСВ, то M(Y)
можно искать по-разному. Если известна
плотность распределения g(y),
то
![]() Если же g(y)
найти сложно, то можно использовать
известную плотность распределения
f(x):
Если же g(y)
найти сложно, то можно использовать
известную плотность распределения
f(x):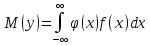 В частности, если все значения Х
принадлежат промежутку (а,
b),
то
В частности, если все значения Х
принадлежат промежутку (а,
b),
то
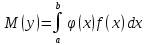
Ф-ция
2ух случ аргументов. Распред суммы
независимых слагаемых. Если
каждой паре возможных значений С величин
Х
и Y
соответствует одно возможное значение
СВ Z,
то Z
называют
функцией
двух случайных аргументов
X
и
Y
: Z
= φ(X,
Y).
Рассмотрим в качестве такой функции
сумму Х
+ Y.
1) Если X
и
Y
–
дискретные независимые
СВ,
то для определения закона распределения
Z
= Х + Y
нужно
найти все возможные значения Z
и
соответствующие им вероятности. 2)
Если X
и
Y
–
непрерывные независимые
СВ,
то, если плотность вероятно-сти хотя бы
одного из аргументов задана на (-∞, ∞)
одной формулой, то плотность суммы g(z)
можно найти по формулам
![]() где f1(x),
f2(y)
– плотности распределения слагаемых.
Если возможные значения аргументов
неотрицательны, то
где f1(x),
f2(y)
– плотности распределения слагаемых.
Если возможные значения аргументов
неотрицательны, то
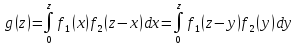 Плотность распределения суммы двух
независимых случайных величин называют
композицией.
Плотность распределения суммы двух
независимых случайных величин называют
композицией.
Устойчивость норм распределен. Закон распред вероятностей называется устойчивым, если композиция таких законов есть тот же закон. В частности, свойством устойчивости обладает норм закон распред: композиция норм законов тоже имеет норм распредел, причем ее мат ожид и дисперсия равны суммам соответствующих характеристик слагаемых.
Нормальный
закон распределения на плоскости.
Нормальным
законом распределения на плоскости
называют распре-деление вероятностей
двумерной случайной величины (X,
Y),
если
![]() *
*![]()
Что называется потоком событий? Потоком событий называ последовательность однородных событий, происходящих в какие-то, вообще говоря, случайные моменты времени.
Какой поток событий называется простейшим потоком?Поток событий назыв простейшим потоком событий, если он обладает след св-вами: стационарность, отсутствие последействия и ординарность:
1. Поток событий называется стационарным, если вер появл одного или нескольких событий на участке времени длины T зависит только от длины T этого участка и не зависит от того, в каком месте оси времени этот участок располагается.
2. Поток событий называется потоком с отсутствием последействия, если события, составляющие поток, появляются в случайные моменты времени независимо друг от друга.
3. Поток событий называется ординарным, если события, составляющие поток, происходят поодиночке, а не парами, тройками и т.д.
Что назыв интенсивностью потока событий? Интенсивностью потока событий называ среднее число событий, происходящих в единицу времени.
З!. Простейший поток событий обладает постоянной интенсив-
ностью.
Какая СМО называется многоканальной СМО?Если в СМО одновременно может обслуживаться несколько заявок,
то СМО называется многоканальной
Как классифицируются СМО? -Если в СМО одновременно может обслуживаться несколько заявок, то СМО назыв многоканальной, в противном случае СМО назыв
одноканальной.
· Как одноканал СМО, так и многоканал СМО делятся на
СМО с отказами и СМО с очередью (ожиданием).
· СМО с очередью различаются по принципу построения очереди.
· СМО с очередью делятся также на СМО с неогранич ожиданием и СМО с ограниченным ожиданием.
Что называется абсолютной пропускной способностью СМО?Абсолютной пропускной способностью СМО называется среднее число заявок, которое может обслужить система за единицу времени.
Что называется относительной пропускной способностью СМО?Относительной пропускной способностью СМО называется средняя доля поступивших заявок, обслуживаемая системой, т.е. отношение среднего числа заявок, которое может обслужить система за единицу времени, к среднему числу заявок, поступивших в систему за это время.
Что
называется приведенной интенсивностью
потока заявок?Приведенная
интенсивность потока
заявок вычисляется по формуле
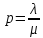
В чем состоит схема расчета показателей эффективности одноканальной СМО с отказами?
Список используемых терминов и обозначений
1 Интенс входящ потока заявок λ
2 Интенс выходящ потока обслуженных заявок μ
3 Приведенная интенс потока заявок ρ
4
Ср
время обслужив заявки
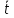 serv
serv
5 Относит пропускная способн СМО q
6 Абсолютная пропускная способность СМО A
7 Вер того, что заявка будет обслужена Pserv
8 Вер того, что заявка получит отказ Potk
Постановка задачи
Параметры λ и μ известны.
Требуется
найти
 serv,
ρ,
q
,
A,
Pserv
,
Potk
.
serv,
ρ,
q
,
A,
Pserv
,
Potk
.
Ф-лы для расчетов:
показатели
эффективности:
![]()
В чем состоит схема расчета показателей эффективности многокан СМО с отказами?
Список используемых терминов и обозначений
1 Число каналов обслуживания n (n >1)
2 Интенс входящего потока заявок λ
3 Интенс потока обслуженных заявок, выходящего из одного канала μ
4 Приведенная интенс потока заявок ρ
5 Вер того, что занято 0, 1, …, n каналов, соответственно P0 ,P1,..., Pn
6 Относит пропускная способность СМО q
7 Абсолютн пропускная способность СМО A
8 Вер того, что заявка будет обслужена Pserv
9 Вер того, что заявка получит отказ P otk
10
Среднее
число занятых каналов
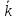
Постановка задачи
Параметры n , λ и μ известны.
Требуется
найти ρ,
p0,
p1,...,
pn
,
P
otk , q
,
A,
Pserv
,
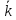 .
.
Формулы для расчетов
Приведенная
интенс
потока
заявок
![]() Вероятности
p0,
p1,...,
pn
вычисл
по формулам
Эрланга:
Вероятности
p0,
p1,...,
pn
вычисл
по формулам
Эрланга:
![]() Поскольку
заявка получает отказ,
если
все каналы обслуживания заняты,
то
Поскольку
заявка получает отказ,
если
все каналы обслуживания заняты,
то
![]()