Биномиальное распределение.

Вернемся к схеме независимых испытаний и найдем закон распределения случайной величины Х – числа появлений события А в серии из п испытаний. Возможные значения А: 0, 1, …, п. Соответствующие им вероятности можно вычислить по формуле Бернулли: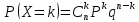

(p – вероятность появления А в каждом испытании). Такой з-н распред назыв биномиальным.

Распределение Пуассона. Рассмотрим ДСВ Х, принимающую только целые неотрицат знач (0, 1, 2,…, т,…), последовательность которых не ограничена. Такая СВ называется распределенной по закону Пуассона, если вер того, что она примет знач т, выражается формулой: где а – некоторая положит величина, называемая параметром закона Пуассона.

Плотность распред непрерывной СВ. Ф-ция f(x), называемая плотностью распределения непрерывной СВ, определ по формуле: f(x)=F′(x),  т.е. является производной функции распределения.

Св-ва плотности распределения.

1) f(x) ≥ 0

2) F(x)=

3) Вер попадания СВ в интервал (а, b) определ ф-лой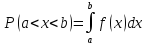 

4)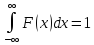 (усл нормировки)

5)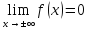, т.к. F(x)->const, при x->±∞

Равномерное распредел вероятностей.Равномерный закон распределения.

Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение ( f(x) = const при a ≤ x ≤ b, f(x) = 0 при x < a, x > b. Вид функции распределения для нормального закона:

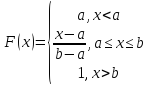
Нормальный з-н распред вероятностей. Нормальная кривая. Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность распределения имеет вид: .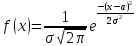

График плотности норм распред называют нормальной кривой (кривой Гаусса). Выясним, какой вид имеет эта кривая, для чего исследуем функцию f(x)

1)  Область опред этой ф-ции: (-∞, +∞).

2) f(x) > 0 при любом х

3)Ось х-горизонтальн асимптота графика

4)Найдя 1ую производную найдём т. mах (а, )

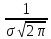5)График симметричен относ прямой а, тогда примерный вид прямой Гаусса:

Ф-ция Лапласа. Вычисление вероятности попадания в заданный интервал нормальной СВ.

Норм распред с параметрами а = 0, σ = 1 назыв нормированным, а его функция распределения -функцией Лапласа.

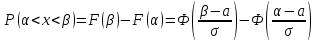
Правило трёх сигм: если СВ распределена нормально, то модуль ее отклонения от х = а не превосходит 3σ.

Показательное распределение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью тогда ф-ция распред F(x)=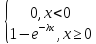, тогда вер попадания показательно распределенной случайной величины в интервал (а, b):

Функция надёжности. Показательный закон надёжности. Пусть элемент начинает работать в момент времени t₀ = 0 и должен проработать в теч периода времени t. Обозначим за Т непрерывную СВ – время безотказной работы элемента,тогда ф-ция F(t) = p(T > t) определяет вер отказа за время t. =>,вер безотказной работы за это же время = R(t) = p(T > t) = 1 – F(t). Эта функция называется функцией надежности. Показательный закон надежности. Часто длительность безотказной работы элемента имеет показательное распределение, т.е  F(t) = 1 – e^-λt => функция надежности в этом случае имеет вид:R(t) = 1 – F(t) = 1 – (1 – e^-λt) = e^-λt Показательным законом надежности называют функцию надежности, определяемую равенствомR(t) = e^-λt , где λ – интенсивность отказов.

Основные числовые характерист ДСВ: мат ожид, св-ва и примеры. Мат ожид ДСВ назывется сумма произведений ее возможных знач на соответств е им вероятности: М(Х) = х₁р₁ + х₂р₂ + … + х_пр_п .           

Если число возможных значений случайной величины бесконечно, то

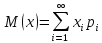
Свойства мат ожид.

1) Мат ожид постоянной равно самой постоянной: М(С) = С. 2) Пост мн-тель можно выносить за знак мат ожид: М(СХ) = С М(Х). 

Две СВ назыв независимыми, если з-н распред одной из них не зависит от того, какие значения приняла другая. В противном случае СВ зависимы.

Назовем произведением независимых СВ Х и Y СВ XY, возможные значения которой = произведениям всех возможных знач Х на все возможные знач Y, а соответствующие им вероятности = произвед вер сомножителей. 3) Мат ожид произведения двух независимых СВ = произведению их мат ожид: M(XY) = (X)M(Y). 

4) Мат ожид суммы двух СВ равно сумме мат ожид слагаемых M (X + Y) = M (X) + M (Y).     

Основные числовые характерист ДСВ: дисперсия и среднее квадратическое отклонение, свойства и примеры. Дисперсией СВ называется мат ожид квадрата ее отклонения от ее мат ожид: D(X) = M (X – M(X))².      Cвойства дисперсии. 1) Дисперсия пост вел С=0: D (C) = 0.     2) Пост множитель можно выносить за знак дисперсии, возведя его в квадрат: D(CX) = C²D(X).   3) Дисперсия суммы 2ух независ СВ = сумме их дисперсий:D(X + Y)=D(X) + D(Y).  Сл 1. Дисперсия суммы нескольких взаимно независ СВ=сумме их дисперсий. 4) Дисперсия разности 2ух независ СВ равна сумме их дисперсий D(X – Y) = D(X) + D(Y). Средним квадратич отклонением σ СВ Х называется квадратный корень из дисперсии: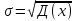

               

 

Xi	0	1
pi	q	p

Числовые характеристики СВ, имеющих стандартные законы распределения. 1. Биномиальное распред. Для ДСВ Х, представляющей собой число появлений события А в серии из п независ испытаний, М(Х) можно найти, используя св-во 4 мат ожид (M (X + Y) = M (X) + M (Y))   Пусть Х₁ – число появлений А в первом испытании, Х₂ – во втором и т.д. При этом каждая из СВ Х_i задается рядом распредел вида  

=>, М(Х_i) = p. Тогда М(Х_i)=p, тогда М(Х)=n!p, Д(х)=npq 2. Закон Пуассона Если р(Х = т) = , то М(х)=a, Д(х)=a²+a-a²=a 3. Равномерное распределение Для равномерно распределенной на отрезке [a, b]  непрерывной СВ 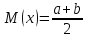, 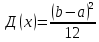4. Нормальное распределение Для вычисления мат ожид нормально распределенной СВ воспользуемся тем, что интеграл Пуассона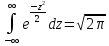 М(х)=а, Д(х)=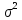Параметры норм распред (а и σ) равны соответственно мат ожид и срквадратич отклонению исследуемой СВ.

Основные характеристики непрерывных СВ: мат ожид, св-ва и примеры. Мат ожид непрерывной СВ называется

Y		Х
		x1		x2	…	xi	…	xn
y1	p(x1,y1)		p(x2,y1)	…	p(xi,y1)	…	p(xn,y1)
…	…		…	…	…	…	…
yj	p(x1, yj)		p(x2, yj)	…	p(xi,yj)	…	p(xn,yj)
…	…		…	…	…	…	…
Ym	p(x1,ym)		p(x2, ym)	…	p(xi,ym)	…	p(xn,ym)

Дискретные двумерные СВ. Закон распределения дискретной двумерной СВ (Х, Y)  имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p(x_i, y_j), с которыми величина принимает значение (x_i, y_j): При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1. Зная закон распред двумерной СВ, можно найти законы распредел ее составляющих. Действительно, событие Х = х₁ представляется собой сумму несовместных событий (X = x₁, Y = y₁), (X = x₁, Y = y₂),…, (X = x₁, Y = y_m), поэтому р(Х = х₁) = p(x₁, y₁) + p(x₁, y₂) +…+ p(x₁, y_m).

Непрерывные двумерные СВ. Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y: F( х, у ) = p ( X < x, Y < y ).  З!. Определение функции распред справедливо как для непрерывной, так и для дискретной двумерной СВ. Свойства функции распределения. 1) 0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью). 2)F(x, y) есть неубыв функция по каждому аргументу:  F(x₂, y) ≥ F(x₁, y), если x₂ > x₁; F(x, y₂) ≥ F(x, y₁),если y₂>y₁. 3)Имеют место предельные соотношения: а) F(-∞, y) = 0; b) F(x, - ∞) = 0; c) F(- ∞, -∞) = 0; d) F( ∞, ∞) =1. 4)  При у = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Х: F(x,  ∞) = F₁(x). При х = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Y : F( ∞, y) = F₂(y).

Ф-ция распред двум СВ, св-ва. Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y: F( х, у ) = p ( X < x, Y < y ).  Св-ва функции распределения. 1) 0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью). 2)F(x, y) есть неубыв функция по каждому аргументу:  F(x₂, y) ≥ F(x₁, y), если x₂ > x₁; F(x, y₂) ≥ F(x, y₁),если y₂>y₁. 3)Имеют место предельные соотношения: а) F(-∞, y) = 0; b) F(x, - ∞) = 0; c) F(- ∞, -∞) = 0; d) F( ∞, ∞) =1. 4)  При у = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Х: F(x,  ∞) = F₁(x). При х = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Y : F( ∞, y) = F₂(y).

Плотность распред. двумерной СВ, св-ва. Плотностью совместного распределения вероятностей (двумер-ной плотностью вероятности) непрерывной двумерной СВ называется смешанная частная производная 2-го порядка от функции распределения: 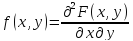Св-ва двумерной плотности вероятности: 1) f(x, y) ≥ 0 2) 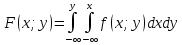3)

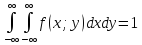
Y		Х
		x1		x2	…	xi	…	xn
y1	p(x1,y1)		p(x2,y1)	…	p(xi,y1)	…	p(xn,y1)
…	…		…	…	…	…	…
yj	p(x1, yj)		p(x2, yj)	…	p(xi,yj)	…	p(xn,yj)
…	…		…	…	…	…	…
Ym	p(x1,ym)		p(x2, ym)	…	p(xi,ym)	…	p(xn,ym)

Закон распределения вероятностей дискретной двумерной СВ. Закон распределения дискретной двумерной СВ (Х, Y)  имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p(x_i, y_j), с которыми величина принимает значение (x_i, y_j): Сумма вероятностей, стоящих во всех клетках таблицы, равна 1. Зная закон распред двумерной СВ, можно найти законы распредел ее составляющих. Действительно, событие Х = х₁ представляется собой сумму несовместных событий (X = x₁, Y = y₁), (X = x₁, Y = y₂),…, (X = x₁, Y = y_m), поэтому р(Х = х₁) = p(x₁, y₁) + p(x₁, y₂) +…+ p(x₁, y_m).

Вер попадания случайной точки в произвольную область. Пусть в пл-ти Оху задана произвольная область D. Найдем вер того, что точка, координаты которой представляют собой систему двух СВ с плотностью распред f(x, y), попадет в область D. Разобьем эту область прямыми, паралл осям координат, на прямоугольники со сторонами Δх и Δу. Вер попадания в каждый такой прямоугольник равна 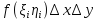, где 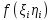- координаты точки, принадлеж прямоугольнику. Тогда вер попадания точки в область D  есть предел интегральной суммы 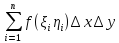, т.е. .

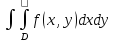Отыскание плотностей вероятности составляющих двумерной СВ. По определению плотности распределения: Аналогично находится