
- •Случайные события. Алгебра событий.
- •Классич определел вероятности. Основные св-ва вероятности.
- •Теор умнож вер. Независимые события.
- •Формула полной вероятности.
- •Биномиальное распределение.
- •Равномерное распредел вероятностей.Равномерный закон распределения.
- •Равномерное распредел на пл-ти.
- •В чем состоит схема расчета показателей эффективности одноканальной смо с ограниченной очередью?
Предмет тер вера. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет тер вера. Осн. интуитивным понятием классической теории вер является случайное событие. События, которые могут произойти в результате опыта, можно подразделить на три вида: а) достоверное событие – событие, которое всегда происходит при провед. опыта; б) невозможное событие – событие, которое в результате опыта произойти не может; в) случ событие – событие, которое может либо произойти, либо не произойти.
Случайные события. Алгебра событий.
Случ событие – событие, которое может либо произойти, либо не произойти.
Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий назыв событие, заключ в том, что произошло хотя бы одно из этих событий.
Произвед АВ соб. А и В назыв событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произвед нескольких событий назыв соб, заключ в том, что произошли все эти события.
Разностью А\B соб А и В назыв событие, состоящее в том, что А произошло, а В – нет.
События А и В назыв совместными, если они могут произойти оба в результате одного опыта. В противном случае события назыв несовместными.
Говорят, что события А1, А2,…,Ап образуют полную группу, если в результате опыта обязател. произойдет хотя бы одно из событий этой группы.
События назыв равновозможными, если нет оснований считать, что одно из них явл более возможным, чем другое.
Относительная
частота и вероятность случайного
события. Статическое определ вероятности.
Для
этого введем вначале понятие относительной
частоты
W(A)
события A
как отношения числа опытов, в которых
наблюдалось событие А, к общему количеству
проведенных испытаний:
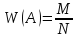 , где N
– общее число опытов, М
– число появлений события А.
Статистической вероятн события
считают его относительную частоту или
число, близкое к ней.
, где N
– общее число опытов, М
– число появлений события А.
Статистической вероятн события
считают его относительную частоту или
число, близкое к ней.
Классич определел вероятности. Основные св-ва вероятности.
Если все события, которые могут произойти в рез-те данного опыта, а) попарно несовместны; б) равновозможны; в) образуют полную группу, то говорят, что имеет место схема случаев.
Вероятностью
события А называется
отношение числа исходов опыта,
благоприятных этому событию, к числу
возможных исходов:
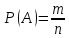 -
классическое
определение вероятности,
где n-число
возможных исходов, m-
число благоприятных исходов.
-
классическое
определение вероятности,
где n-число
возможных исходов, m-
число благоприятных исходов.
Свойства вероятности.
1. Вероятн достоверн. события= 1.
2. Вероятн. невозможного соб=0. 3. Вер. случ события есть положит число, заключенное м-ду 0 и 1.
Основные
формулы комбинаторики. Комбинаторика
– наука, изучающая комбинации, которые
можно составить по определ правилам из
элементов некоторого конечного множества.
Перестановки
–
это комбинации, составленные из всех п
элементов данного множества и отличающиеся
только порядком их располож. Число всех
возможных перестановок Рn=n!
Размещения
– комбинации из т
элементов множества, содержащего п
различных элементов, отличающиеся либо
составом элементов, либо их порядком.
Число всех возможных размещений
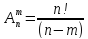 .
Сочетания
– неупорядоченные наборы из т
элементов множества, содержащего п
различных элементов (то есть наборы,
отличающиеся только составом элементов).
Число сочетаний
.
Сочетания
– неупорядоченные наборы из т
элементов множества, содержащего п
различных элементов (то есть наборы,
отличающиеся только составом элементов).
Число сочетаний

Геометрические
вероятности. Одним
из недостатков классического определения
вероятности является то, что оно
неприменимо к испытаниям с бесконечным
количеством исходов. В таких случаях
можно воспользоваться понятием
геометрической
вероятности.
Пусть на отрезок L
наудачу брошена точка. Это означает,
что точка обязательно попадет на отрезок
L
и с равной возможностью может совпасть
с любой точкой этого отрезка. При этом
вероятность попадания точки на любую
часть отрезка L
не
зависит от расположения этой части на
отрезке и пропорциональна его длине.
Тогда вероятность того, что брошенная
точка попадет на отрезок l,
являющийся частью отрезка L,вычисл
по формуле:
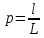 ,где l
–
длина отрезка
l,
а L
–
длина отрезка L.
,где l
–
длина отрезка
l,
а L
–
длина отрезка L.
Теор слож вер. Противоположн события. Условные вероятности.
Теор сложения.Вер р(А + В) суммы событий А и В равна
Р (А + В ) = р (А) + р (В) – р (АВ).
Противоположн
событиями
называют2несовместных события, образующих
полную группу. Если одно из них назвать
А,
то второе принято обозначать
![]() .
.
