
- •Лабораторные работы
- •Содержание
- •2 Теоретические сведения по выполняемым
- •Введение
- •Глава 1 обзор виртуальных лабораторий
- •1.1 Star
- •1.2 Ewb
- •1.3 Simulink
- •1.4 Краткие сведения о пакетах Multisim и Mathcad
- •1.4.1 Multisim
- •1.4.2 Mathcad
- •Глава 2 теоретические сведения по выполняемым лабораторным работам
- •2.1 Гармонические осцилляторы
- •2.2 Сложение гармонических колебаний
- •2.3 Ангармонический осциллятор
- •2.4 Параметрические колебания
- •2.5 Нелинейные волны
- •2.6 Хаотические колебания
- •Глава 3 экспериментальная часть
- •3.1 Гармонические осцилляторы
- •3.1.1 Лабораторная работа «Исследование гармонических колебаний»
- •3.1.2 Лабораторная работа «Исследование затухающих гармонических колебаний»
- •3.1.3 Лабораторная работа «Исследование частотных свойств резонансных контуров»
- •3.2 Сложение гармонических колебаний
- •3.2.1 Лабораторная работа «Сложение однонаправленных колебаний»
- •3.2.2 Лабораторная работа «Сложение перпендикулярных колебаний»
- •3.3 Ангармонические осцилляторы
- •3.3.2 Лабораторная работа «Осциллятор Ван-дер-Поля»
- •3.4 Лабораторная работа «Параметрические колебания»
- •3.4.1 Лабораторная работа «Исследование параметрического усилителя»
- •3.5 Лабораторная работа «Нелинейные волны»
- •3.5.1 Лабораторная работа «Солитоны»
- •3.6 Лабораторная работа «Хаотические колебания»
- •3.6.1 Лабораторная работа «Осциллятор Лоренца»
- •3.6.2 Лабораторная работа «Генератор шума»
- •Заключение
- •Литература
2.5 Нелинейные волны
Наиболее известными и хорошо исследованными нелинейными уравнениями математической физики являются уравнения, описывающие распространение волн в нелинейных средах [14]. Решениями таких уравнений могут быть ударные волны или солитоны – уединенные волны, обладающие свойствами частиц.
Уравнение Буссинеска:
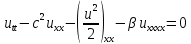 . (2.44)
. (2.44)
Уравнение Кортевега-де Фриза:
 . (2.45)
. (2.45)
Уравнение синус – Гордона:
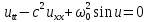 . (2.46)
. (2.46)
Нелинейное уравнение Шредингера:
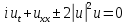 . (2.47)
. (2.47)
В качестве первого шага при исследовании нелинейных волновых уравнений часто ищут решения в виде стационарных бегущих волн, то есть волн, форма которых не зависит от времени.
Рассмотрим уравнение Кортевега-де Фриса (2.45).
Будем искать решение уравнения (2.45) в виде:
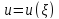 , (2.48)
, (2.48)
где
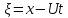 ,
,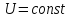 .
.
Преобразовав, имеем:
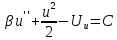 . (2.49)
. (2.49)
Введем новую переменную:
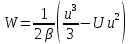 . (2.50)
. (2.50)
Тогда:
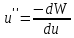 . (2.51)
. (2.51)
Получили
уравнение осциллятора с потенциальной
энергией W.
Тогда
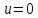 – седло, точка
– седло, точка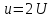 – центр (рис. 2.6).
– центр (рис. 2.6).
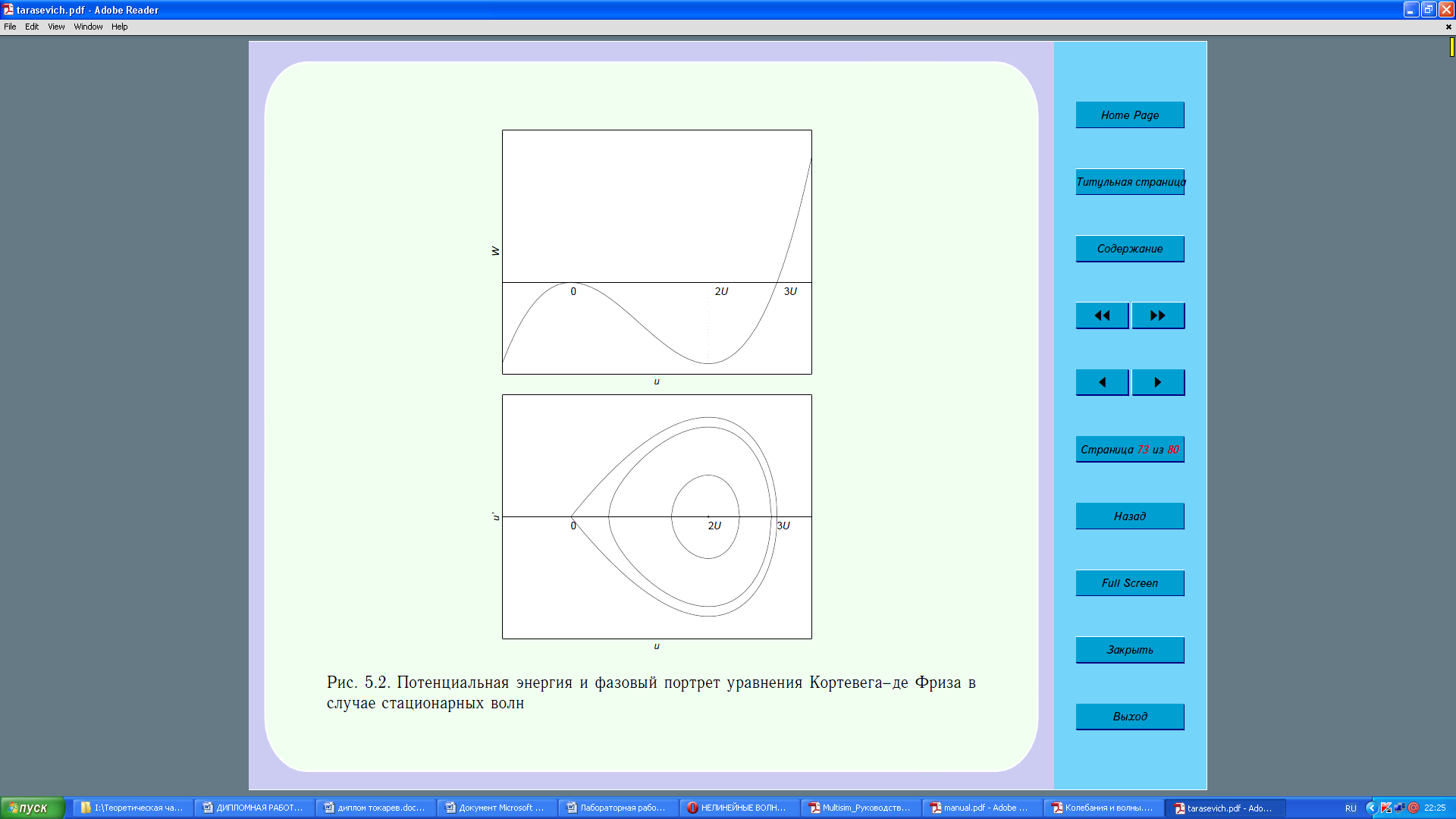
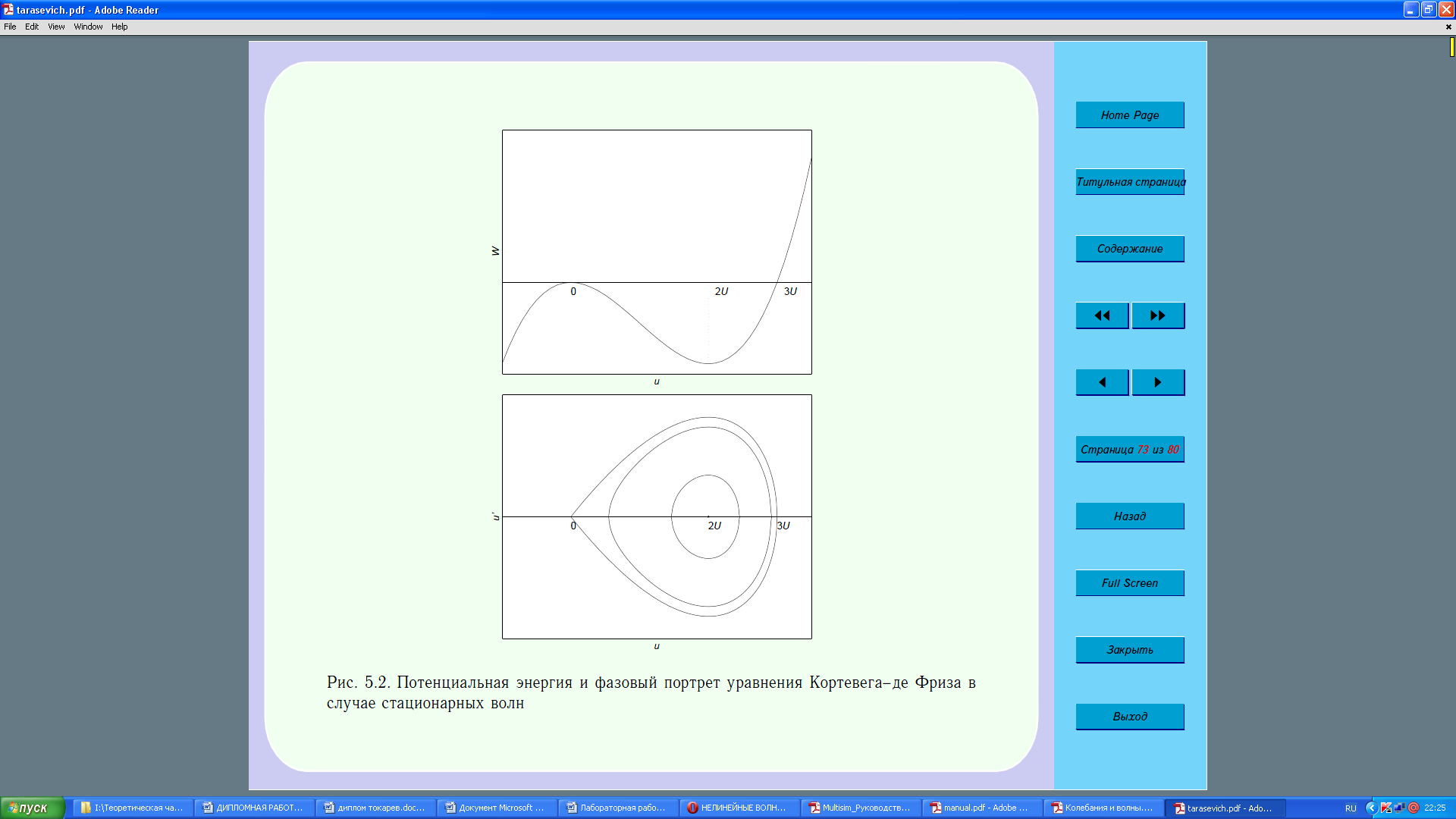
Рис. 2.6 – Потенциальная энергия и фазовый портрет уравнения Кортевега-де Фриза в случае стационарных волн
Волны малой амплитуды будут иметь форму близкую к синусоидальной. Волны большой амплитуды сильно нелинейны, их называют кноидальными. Движению по сепаратрисе соответствует уединенная волна – солитон.
Преобразовав уравнение (2.51) получаем:
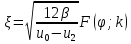 , (2.52)
, (2.52)
где
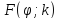 - неполный эллиптический интеграл
первого рода.
- неполный эллиптический интеграл
первого рода.
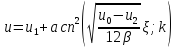 . (2.53)
. (2.53)
Рассмотрим
случай малых колебаний вблизи дна
потенциальной ямы. Тогда
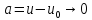 ,
,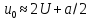 ,
,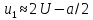 ,
,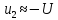 ,
,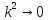 .
Тогда:
.
Тогда:
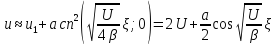 . (2.54)
. (2.54)
Получено уравнение гармонической волны (рис. 2.6).
Рассмотрим
предельный случай
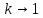 .
Тогда
.
Тогда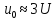 ,
,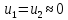 .
.
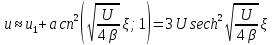 . (2.55)
. (2.55)
Получено
решение в виде солитона – уединенной
волны – с амплитудой
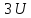 и шириной
и шириной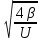 (рис. 2.7).
(рис. 2.7).
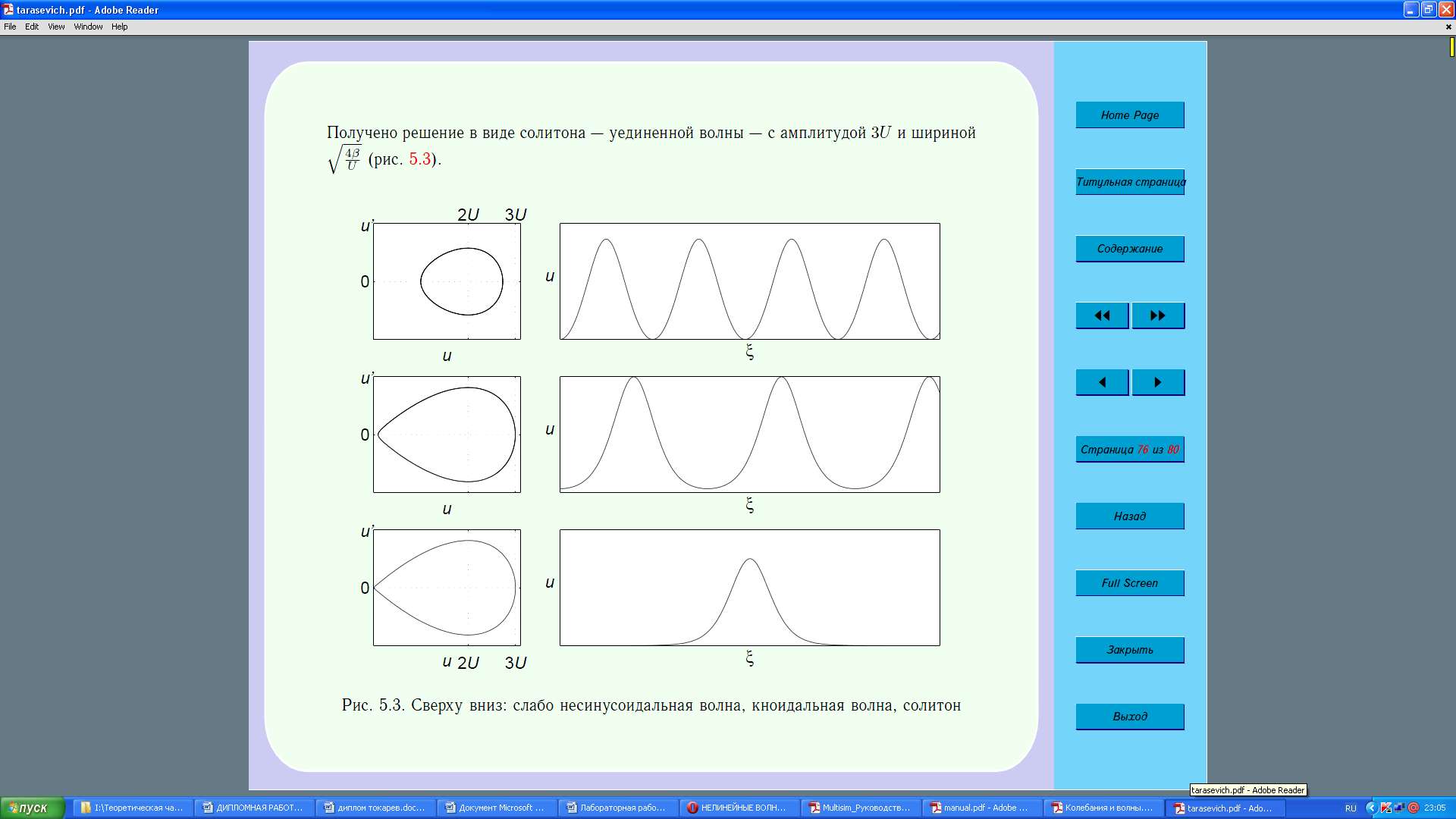
Рис. 2.7 – Сверху вниз: слабо несинусоидальная волна, кноидальная волна, солитон
2.6 Хаотические колебания
Хаотические колебания – это неупорядоченные движения, которые возникают в совершенно детерминированных нелинейных динамических системах различной природы и не связаны с действием на эти системы случайных внешних сил, в том числе и случайных шумов. Представляют собой новый класс движений, который связан часто с состоянием, получившим название странный аттрактор.
Аттрактор Лоренца – это трехмерная система нелинейных автономных дифференциальных уравнений первого порядка вида:
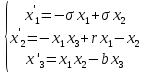 , (2.56)
, (2.56)
где
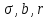 - параметры.
- параметры.
В
результате численного интегрирования
системы (2.56) Лоренц обнаружил, что при
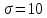 ,
,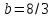 и
и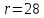 у этой динамической системы, с одной
стороны, наблюдается хаотическое,
нерегулярное поведение всех траекторий
(рис. 2.8), а, с другой стороны, все траектории
притягиваются к некоторому сложно
устроенному множеству – аттрактору.
у этой динамической системы, с одной
стороны, наблюдается хаотическое,
нерегулярное поведение всех траекторий
(рис. 2.8), а, с другой стороны, все траектории
притягиваются к некоторому сложно
устроенному множеству – аттрактору.
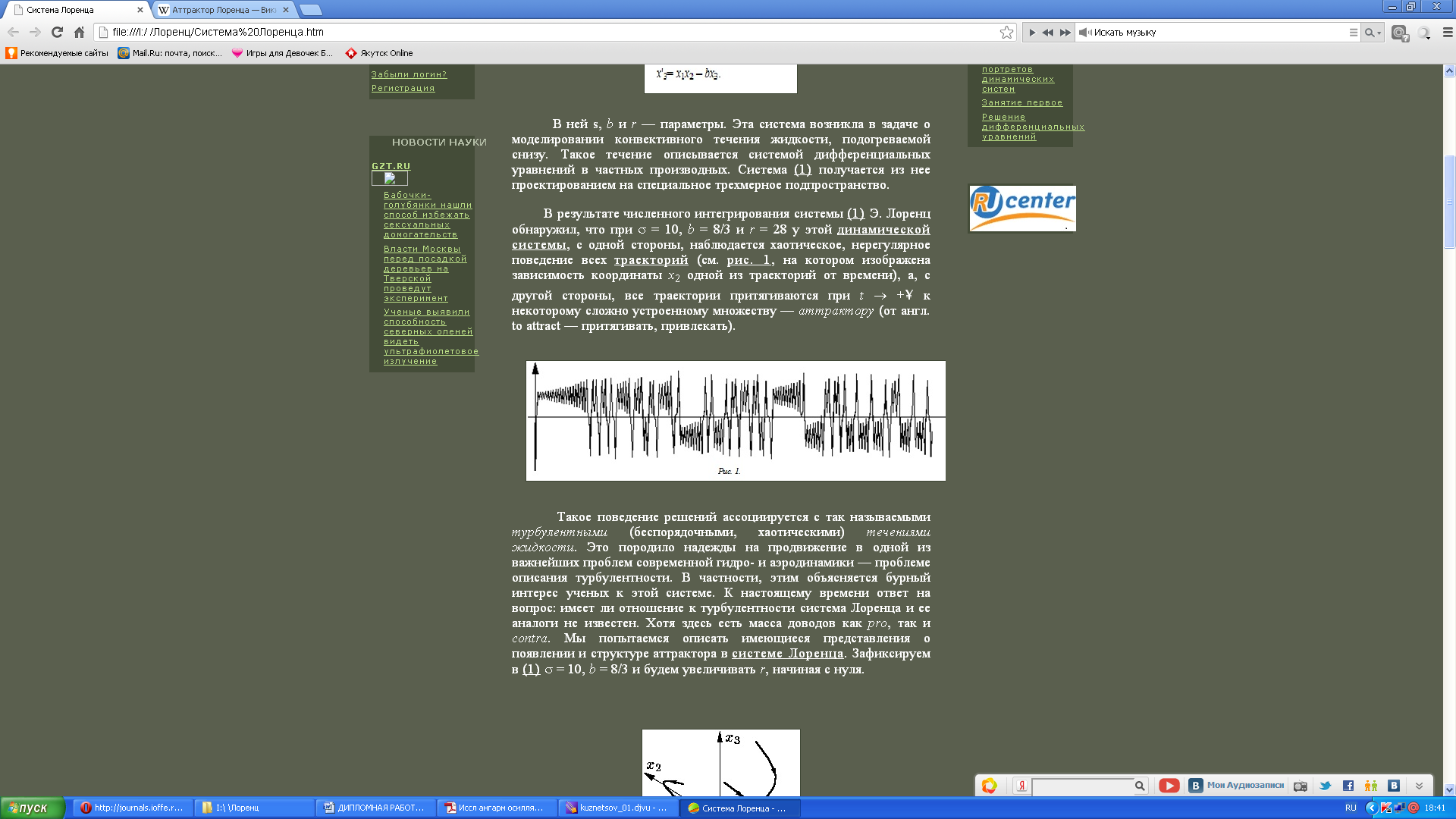
Рис.
2.8 – Зависимость координаты
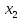 одной из траекторий от времени
одной из траекторий от времени
Зафиксируем
в (2.56)
 ,
,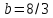 и будем увеличивать
и будем увеличивать ,
начиная с нуля. При
,
начиная с нуля. При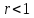 система Лоренца имеет асимптотически
устойчивую в целом стационарную точку
– начало координат. К ней притягиваются
все траектории (рис. 2.9).
система Лоренца имеет асимптотически
устойчивую в целом стационарную точку
– начало координат. К ней притягиваются
все траектории (рис. 2.9).
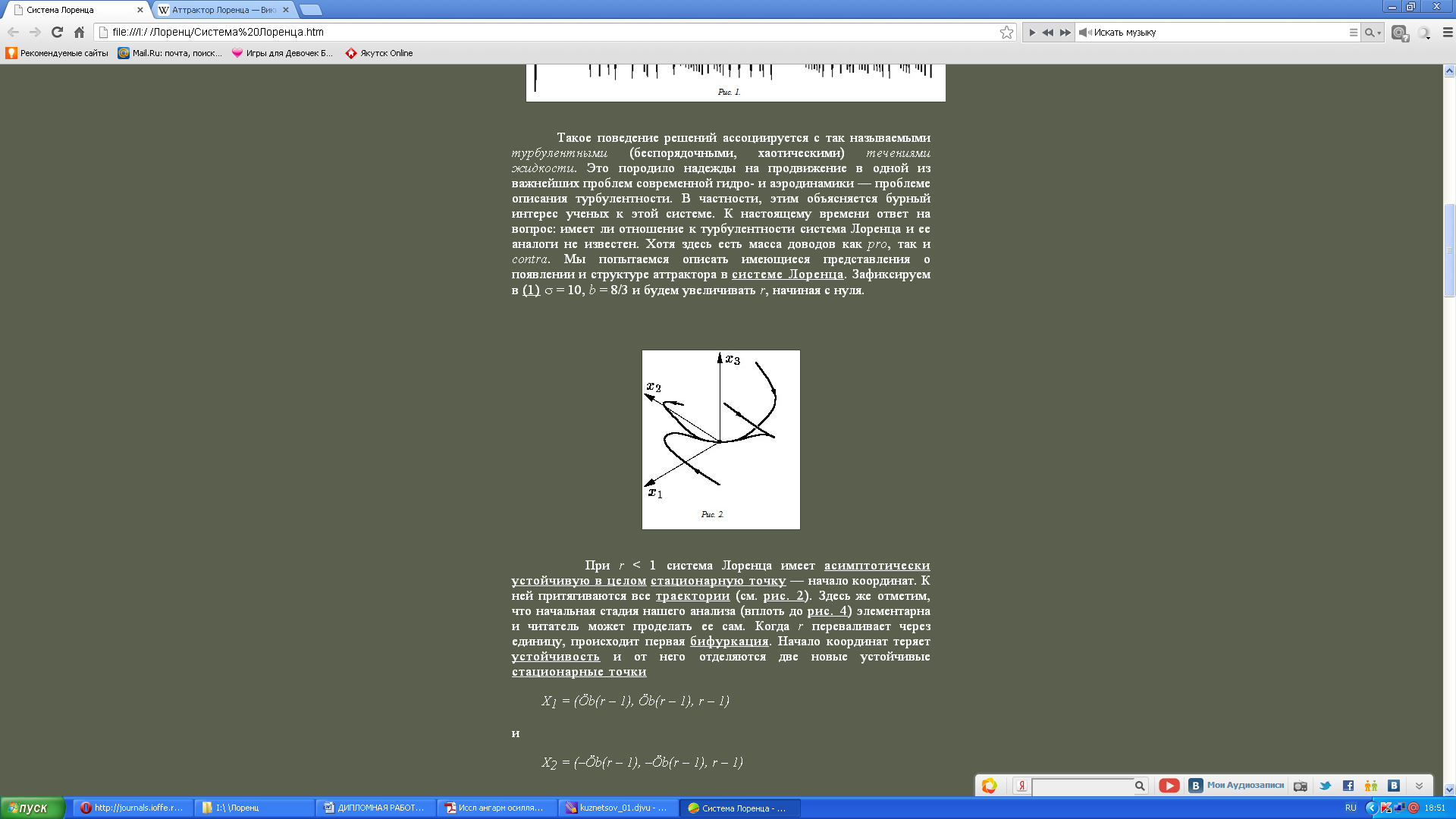
Рис. 2.9 – Траектории системы Лоренца
Когда
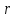 переваливает через единицу, происходит
первая бифуркация. Начало координат
теряет устойчивость и от него отделяются
две новые устойчивые стационарные
точки:
переваливает через единицу, происходит
первая бифуркация. Начало координат
теряет устойчивость и от него отделяются
две новые устойчивые стационарные
точки:
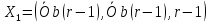 ,
,
 . (2.57)
. (2.57)
У линеаризованной в нулевой стационарной точке системы два отрицательных и одно положительное собственное значение. В соответствии с этим у нулевой стационарной точки есть двумерный входящий ус и одномерный выходящий (рис. 2.10).
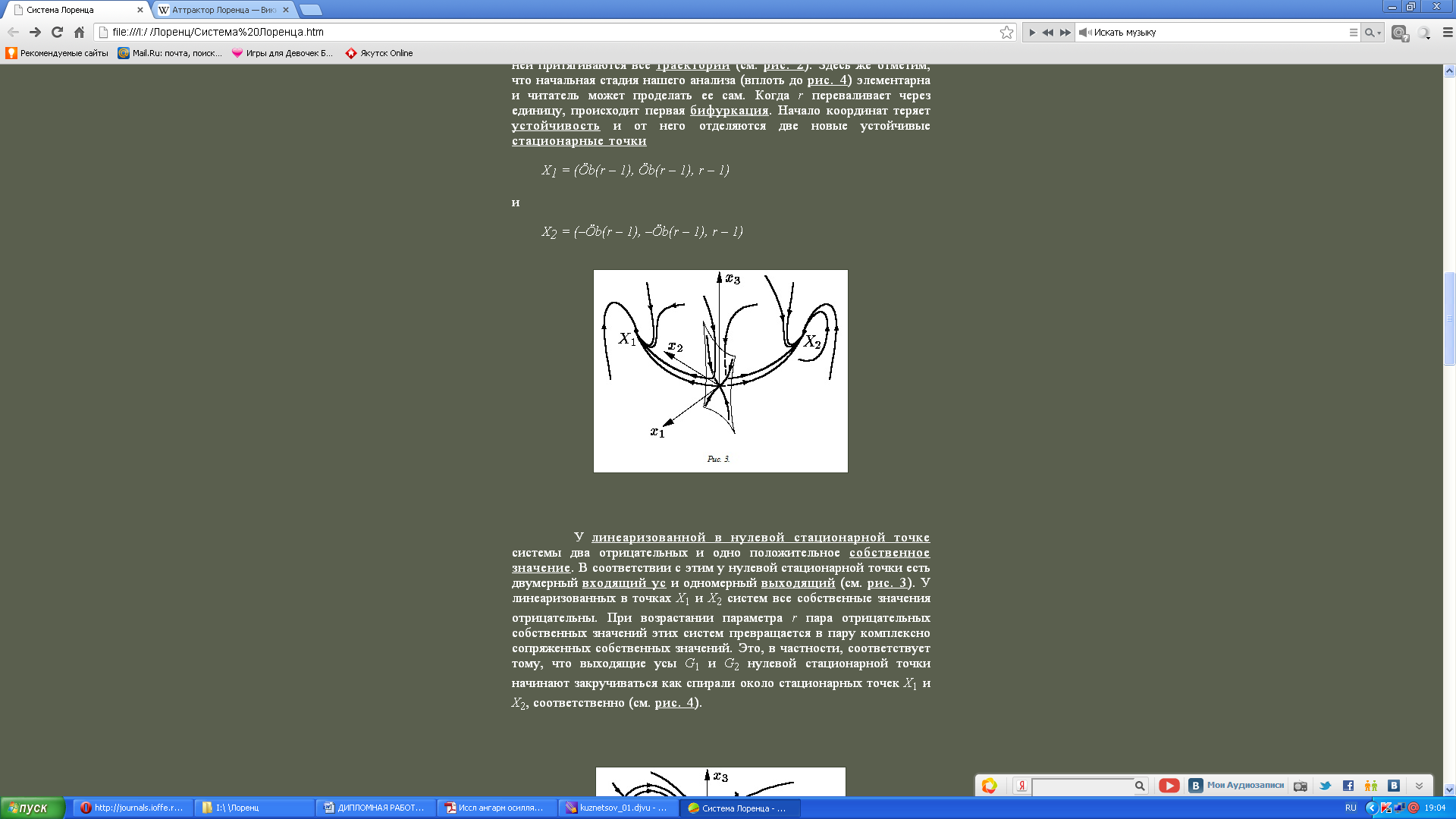
Рис. 2.10 – Траектории линеаризованной системы Лоренца
У
линеаризованных в точках
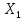 и
и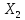 систем все собственные значения
отрицательны. При возрастании параметра
систем все собственные значения
отрицательны. При возрастании параметра пара отрицательных собственных значений
этих систем превращается в пару комплексно
сопряженных собственных значений. Это,
в частности, соответствует тому, что
выходящие усыG1
и G2
нулевой стационарной точки начинают
закручиваться как спирали около
стационарных точек
пара отрицательных собственных значений
этих систем превращается в пару комплексно
сопряженных собственных значений. Это,
в частности, соответствует тому, что
выходящие усыG1
и G2
нулевой стационарной точки начинают
закручиваться как спирали около
стационарных точек
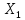 и
и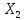 ,
соответственно (рис. 2.11).
,
соответственно (рис. 2.11).
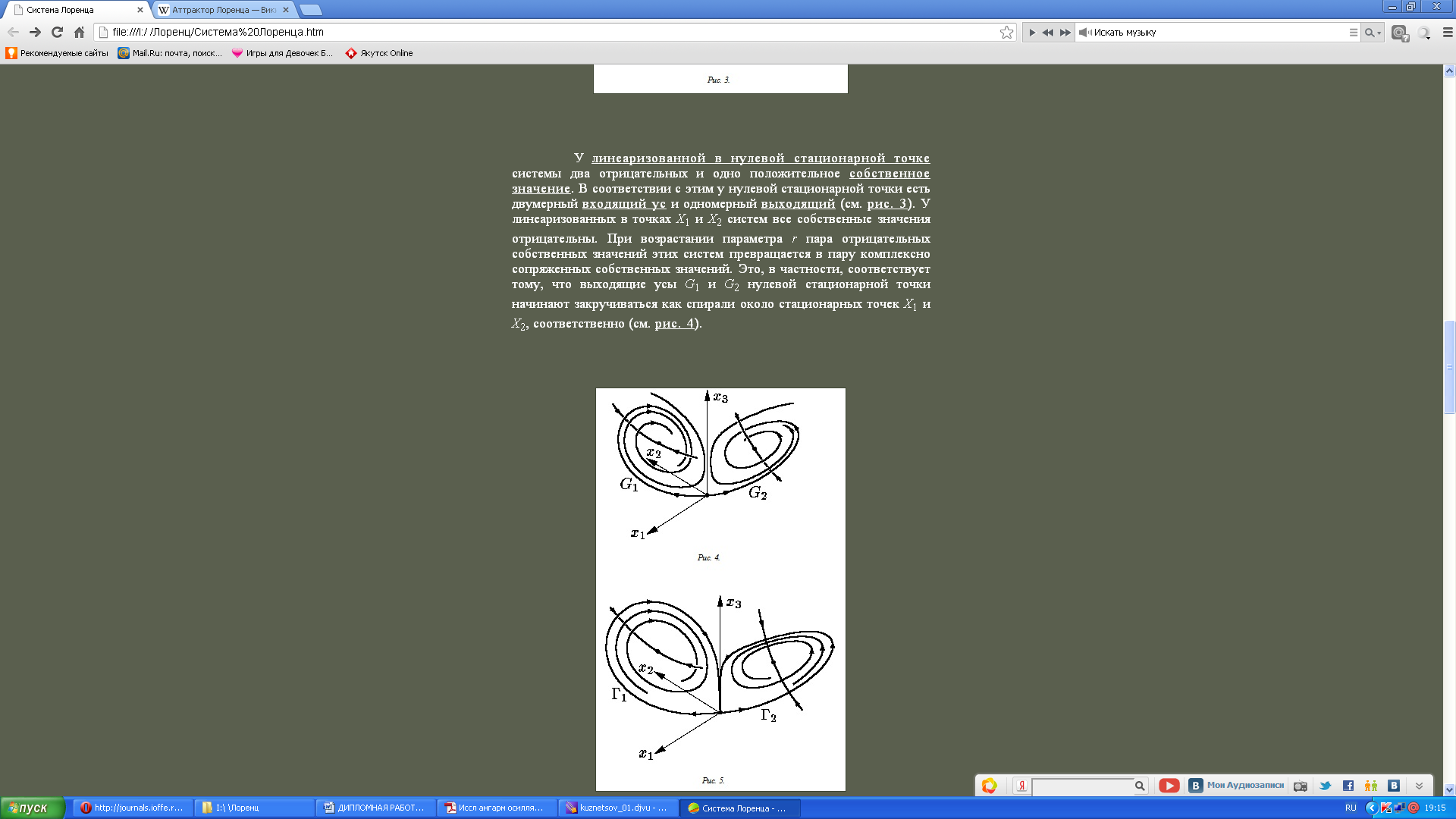
Рис.
2.11 – Траектории системы Лоренца при
возрастании
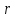
С
дальнейшим ростом
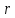 стационарные точки
стационарные точки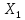 и
и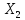 поднимаются выше (они лежат в плоскости
поднимаются выше (они лежат в плоскости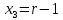 ),
а спиралевидные траектории «разбухают».
Это происходит до тех пор, пока при
),
а спиралевидные траектории «разбухают».
Это происходит до тех пор, пока при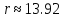 спирали, начинающиеся как выходящие
усы нуля, попадают на его входящий ус,
образуя две гомоклинические траектории
Г1
и Г2
(рис. 2.12).
спирали, начинающиеся как выходящие
усы нуля, попадают на его входящий ус,
образуя две гомоклинические траектории
Г1
и Г2
(рис. 2.12).
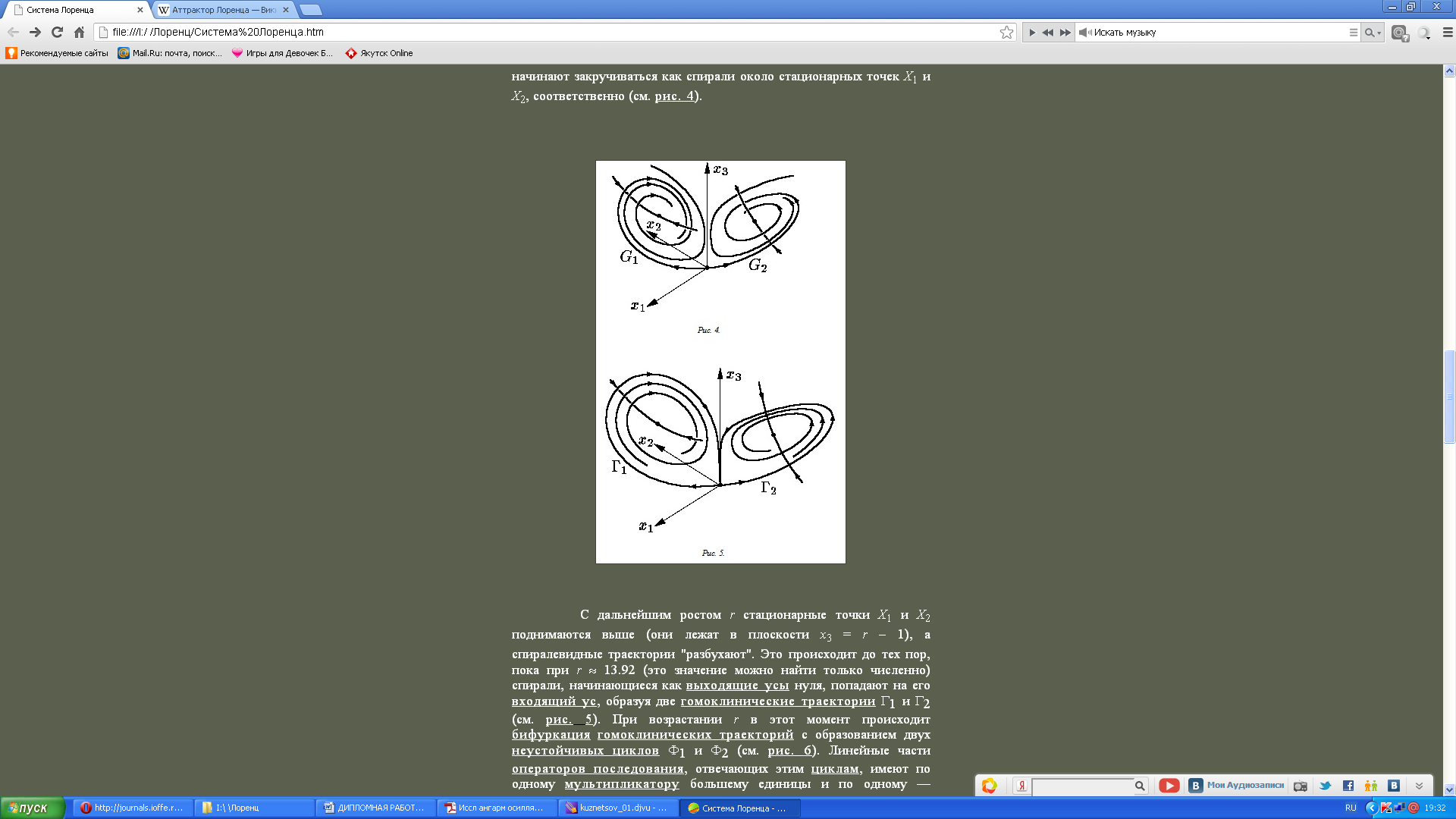
Рис. 2.12 – Гомоклинические траектории системы Лоренца
