
- •Лабораторные работы
- •Содержание
- •2 Теоретические сведения по выполняемым
- •Введение
- •Глава 1 обзор виртуальных лабораторий
- •1.1 Star
- •1.2 Ewb
- •1.3 Simulink
- •1.4 Краткие сведения о пакетах Multisim и Mathcad
- •1.4.1 Multisim
- •1.4.2 Mathcad
- •Глава 2 теоретические сведения по выполняемым лабораторным работам
- •2.1 Гармонические осцилляторы
- •2.2 Сложение гармонических колебаний
- •2.3 Ангармонический осциллятор
- •2.4 Параметрические колебания
- •2.5 Нелинейные волны
- •2.6 Хаотические колебания
- •Глава 3 экспериментальная часть
- •3.1 Гармонические осцилляторы
- •3.1.1 Лабораторная работа «Исследование гармонических колебаний»
- •3.1.2 Лабораторная работа «Исследование затухающих гармонических колебаний»
- •3.1.3 Лабораторная работа «Исследование частотных свойств резонансных контуров»
- •3.2 Сложение гармонических колебаний
- •3.2.1 Лабораторная работа «Сложение однонаправленных колебаний»
- •3.2.2 Лабораторная работа «Сложение перпендикулярных колебаний»
- •3.3 Ангармонические осцилляторы
- •3.3.2 Лабораторная работа «Осциллятор Ван-дер-Поля»
- •3.4 Лабораторная работа «Параметрические колебания»
- •3.4.1 Лабораторная работа «Исследование параметрического усилителя»
- •3.5 Лабораторная работа «Нелинейные волны»
- •3.5.1 Лабораторная работа «Солитоны»
- •3.6 Лабораторная работа «Хаотические колебания»
- •3.6.1 Лабораторная работа «Осциллятор Лоренца»
- •3.6.2 Лабораторная работа «Генератор шума»
- •Заключение
- •Литература
2.3 Ангармонический осциллятор
Уравнение колебаний физического маятника имеет вид [14]:
 , (2.30)
, (2.30)
где
 ;
;
 –масса
маятника;
–масса
маятника;
 –его
момент инерции относительно оси вращения;
–его
момент инерции относительно оси вращения;
 –расстояние
от точки подвеса до центра масс;
–расстояние
от точки подвеса до центра масс;
 –ускорение
свободного падения;
–ускорение
свободного падения;
 –угол
отклонения из положения равновесия.
–угол
отклонения из положения равновесия.
Разложение
 в ряд Тейлора:
в ряд Тейлора:
 =
= (2.31)
(2.31)
При
малых углах отклонения ( )
) и уравнение (2.30) переходит в уравнение
гармонического осциллятора (2.1). Для
уточнения решения можно учесть следующий
член в разложении (2.31), тогда:
и уравнение (2.30) переходит в уравнение
гармонического осциллятора (2.1). Для
уточнения решения можно учесть следующий
член в разложении (2.31), тогда:
 . (2.32)
. (2.32)
Полученное уравнение может быть решено методами теории возмущений в виде:
 . (2.33)
. (2.33)
Если
углы отклонения
 не очень велики, то правую часть уравнения
(2.33) можно считать малой поправкой
(возмущением). При возмущении равном
нулю уравнение (2.33) переходит в (2.1) и его
решение:
не очень велики, то правую часть уравнения
(2.33) можно считать малой поправкой
(возмущением). При возмущении равном
нулю уравнение (2.33) переходит в (2.1) и его
решение:
 . (2.34)
. (2.34)
Решением
возмущенного уравнения является
суперпозиция колебаний с частотами
 и
и .
Решение уравнения (2.30) будет содержать
набор высших гармоник. Наличие в спектре
колебаний с кратными частотами (гармоник)
– наиболее важная характерная черта
нелинейных колебаний.
.
Решение уравнения (2.30) будет содержать
набор высших гармоник. Наличие в спектре
колебаний с кратными частотами (гармоник)
– наиболее важная характерная черта
нелинейных колебаний.
В случае не очень больших колебаний период колебаний равен:
 . (2.35)
. (2.35)
Для произвольных углов:
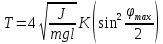 , (2.36)
, (2.36)
где
 , (2.37)
, (2.37)
- полный эллиптический интеграл первого рода.
Уравнение
(2.30) описывает ангармонический осциллятор.
Его решение можно представить в виде
суперпозиции нескольких гармонических
решений. Результаты решения уравнения
(2.30) представлены на рис. 2.4 (зависимость
 )
и на рис. 2.5 (зависимость
)
и на рис. 2.5 (зависимость ).
).

Рис.2.4
– Зависимость


Рис.2.5
– Зависимость

Любопытно поведение ангармонического осциллятора под действием внешней гармонической силы. Наличие в решении высших гармоник приводит к тому, что резонанс может наступить на различных частотах, кратных собственной частоте гармонического осциллятора. Неизохронность колебаний, то есть зависимость периода (частоты колебаний) от амплитуды приводит к тому, что при резонансе собственная частота осциллятора меняется, и он выходит из резонанса.
2.4 Параметрические колебания
Параметрическими колебаниями называются колебания, при которых происходит периодическое изменение какого-либо параметра колеблющейся системы. Если изменение параметра системы к увеличению амплитуды колебаний, то такой процесс называют параметрическим резонансом [15].
Параметрические явления можно рассмотреть на примере с качелями. Если качнуть качели, и сидящий на ней на корточках, в момент поднятия будет привставать, и как только качели перешли мертвую точку, будет садиться, в колебательный контур сообщится энергия равная изменению массы в этот момент. Для сидящего на качелях этот момент будет происходить по инерции, качели сами подкидывают тело, и приседание не вызовет затруднений так как на тело действует гравитация. Суммарная затраченная энергия будет больше, полученной. Но в сумме всех затраченных и полученных энергий кпд за единицу не перевалит. Таким образом мы создали параметрические колебания. Так же их можно создать меняя длину маятника.
Рассмотрим параметрические колебания математического маятника в общем случае, то есть при произвольном характере изменения параметра и больших колебаниях при наличии вязкого трения [14]. Уравнение движения маятника – уравнение динамики вращательного движения:
 . (2.38)
. (2.38)
Момент импульса:
 . (2.39)
. (2.39)
На
систему действует два момента сил:
момент силы тяжести -
 и момент силы трения –
и момент силы трения –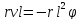 ,
где
,
где – коэффициент трения. Тогда уравнение
движения принимает вид:
– коэффициент трения. Тогда уравнение
движения принимает вид:
 . (2.40)
. (2.40)
Это
нелинейное дифференциальное уравнение
второго порядка описывает самый общий
случай параметрических колебаний. В
случае малых колебаний (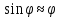 )
заменой переменных
)
заменой переменных ,
где
,
где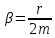 ,
уравнение приводится к виду:
,
уравнение приводится к виду:
 , (2.41)
, (2.41)
где
 и
и .
.
Уравнение
(2.41) – дифференциальное уравнение
второго порядка с периодическим
коэффициентом
 называется уравнением Хилла.
называется уравнением Хилла.
В частном случае, если:
 , (2.42)
, (2.42)
где
 ,
то
,
то и уравнение Хилла можно преобразовать
к уравнению Матьё:
и уравнение Хилла можно преобразовать
к уравнению Матьё:
 . (2.43)
. (2.43)
Считая,
что затухание отсутствует,
 и
и .
.
