Глава 2 теоретические сведения по выполняемым лабораторным работам

2.1 Гармонические осцилляторы

Гармонический осциллятор – это система, уравнение движения которой описывается дифференциальным уравнением:

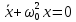, (2.1)

где - величина, совершающая колебания;

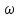–циклическая частота.

Колебания гармонического осциллятора есть важный пример периодического движения [10]. В качестве примеров гармонического осциллятора могут быть пружинный, физический и математический маятники, колебательный контур (для малых токов и напряжений).

1. Пружинный маятник - это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы:

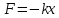, (2.2)

где 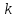- жесткость пружины.

Уравнение движения маятника имеет вид:

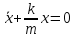. (2.3)

Из формулы (2.1) вытекает, что пружинный маятник совершает гармонические колебания по закону:

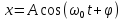, (2.4)

с циклической частотой:

, (2.5)

и периодом:

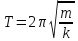. (2.6)

Формула (2.6) верна для упругих колебаний в границах, в которых выполняется закон Гука, т.е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2.5) и формулу потенциальной энергии, равна:

. (2.7)

2. Физический маятник - это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела (рис. 2.1).

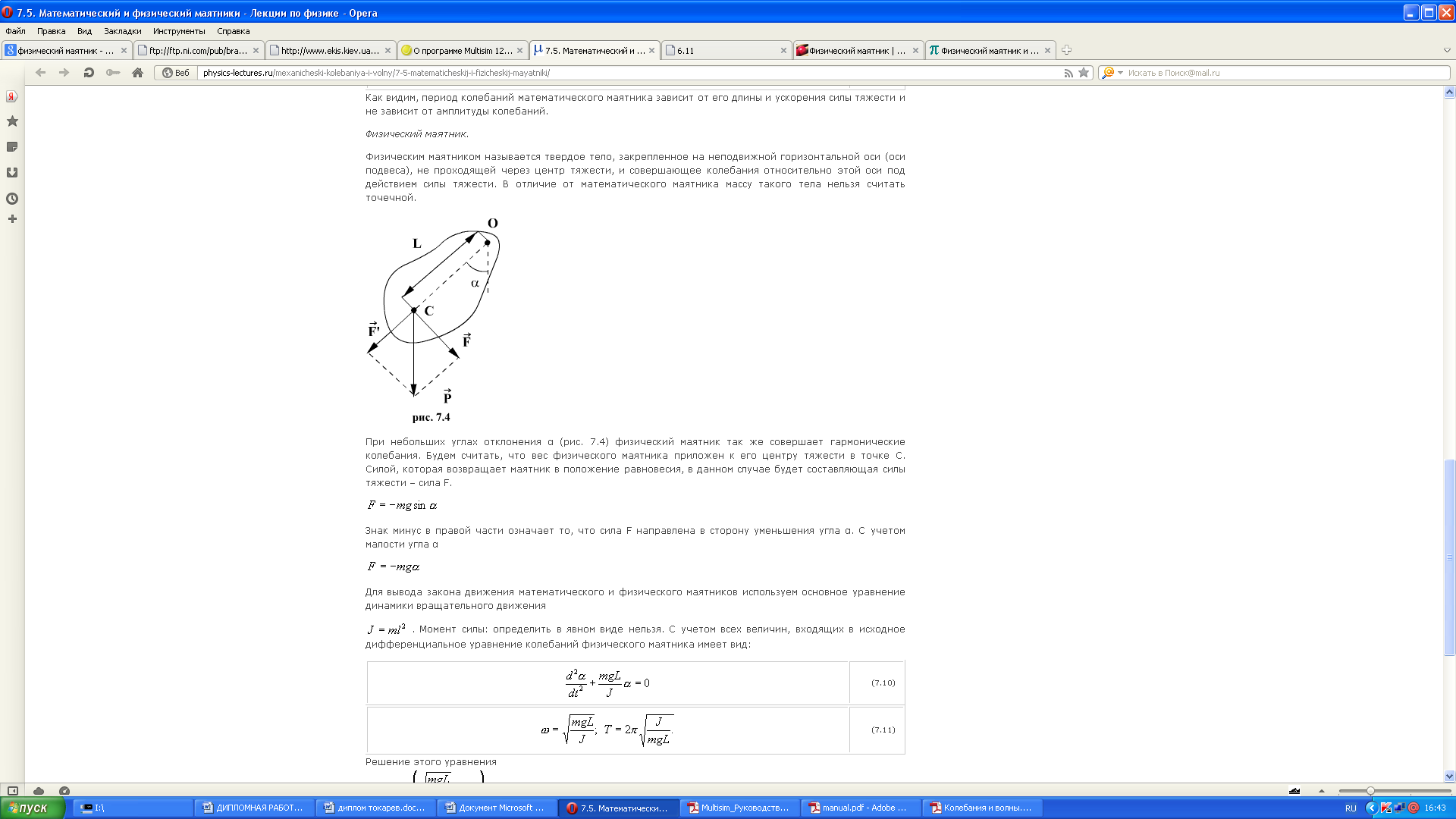
Рис. 2.1 – Физический маятник

Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы:

, (2.8)

где 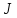- момент инерции маятника относительно оси, которая проходит через точку подвеса О;

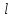- расстояние между осью и центром масс маятника;

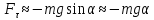–возвращающая сила (знак минус указывает на то, что направления ивсегда противоположны;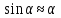поскольку колебания маятника считаются малыми, т.е. маятник из положения равновесия отклоняется на малые углы).

Уравнение (2.8) запишем как:

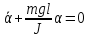. (2.9)

Принимая

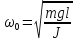, (2.10)

получим уравнение:

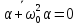, (2.11)

идентичное с (2.1), решение, которого (2.1) найдем и запишем как:

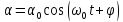. (2.12)

Из формулы (2.12) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой 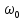и периодом:

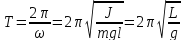, (2.13)

где введена величина 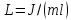- приведенная длина физического маятника.

Точка О' на продолжении прямой ОС, которая отстоит от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 2.1). Применяя теорему Штейнера для момента инерции оси, найдем:

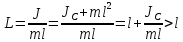, (2.14)

т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника.

3. Математический маятник - это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника:

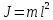, (2.15)

где 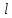- длина маятника.

Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке - центре масс, то, подставив (2.15) в (2.13), найдем выражение для периода малых колебаний математического маятника:

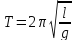. (2.16)

Сопоставляя формулы (2.13) и (2.16), видим, что если приведенная длина L физического маятника равна длине математического маятника, то периоды колебаний этих маятников одинаковы. Значит, приведенная длина физического маятника - это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника.