3.3.2 Лабораторная работа «Осциллятор Ван-дер-Поля»
Цель работы: исследование осциллятора Ван-дер-Поля на пакете Mathcad.
Заданные значения: µ=0,±1,±10; β=№ варианта от 1 до 25; y0 = 0,±1,±10.
Набрать на пакете Mathcad программу, приведенную на рисунке 3.23, и меняя значения µ, β, y0 получить временные и фазовые характеристики.
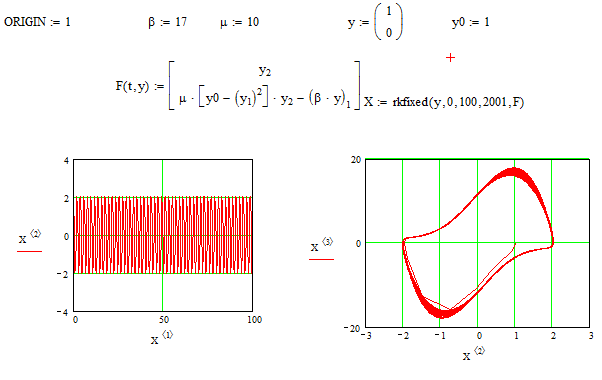
Рис. 3.23 – Программа осциллятора Ван-дер-Поля, где Х(1)- время, Х(2)- амплитуда, Х(3)- ускорение
Пример выполнения лабораторной работы:
Заданные значения: µ=0,±1,±10; β=±17; y0 = 0,±1,±10.
При β=17, μ=1, y0=1 (рис. 3.24).
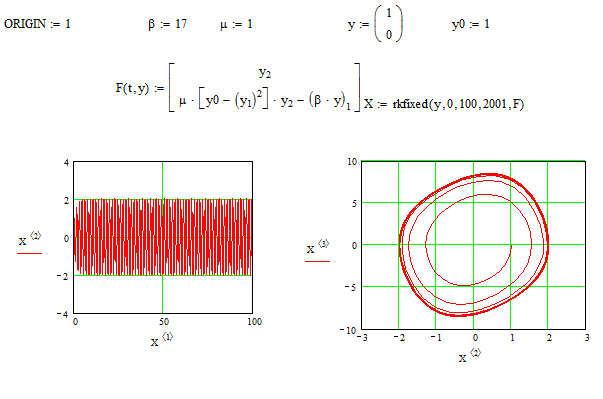
Рис. 3.24 - Программа осциллятора Ван-дер-Поля при β=17, μ=1, y0=1
При β=17, μ=1, y0=-1 (рис. 3.25).
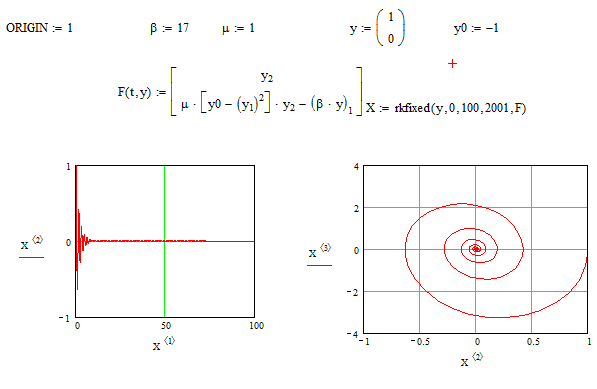
Рис. 3.25 - Программа осциллятора Ван-дер-Поля при β=17, μ=1, y0=-1
При β=17, μ=1, y0=10 (рис. 3.26).
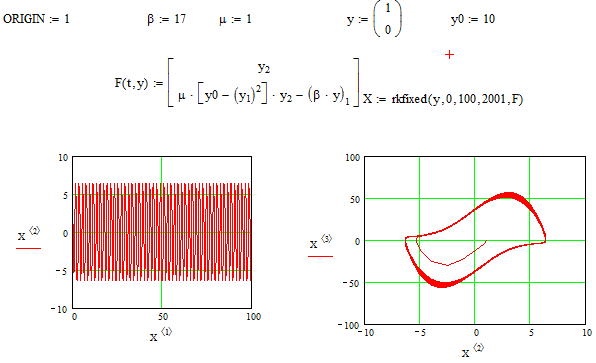
Рис. 3.26 - Программа осциллятора Ван-дер-Поля при β=17, μ=1, y0=10
При β=17, μ=1, y0=0 (рис. 3.27).
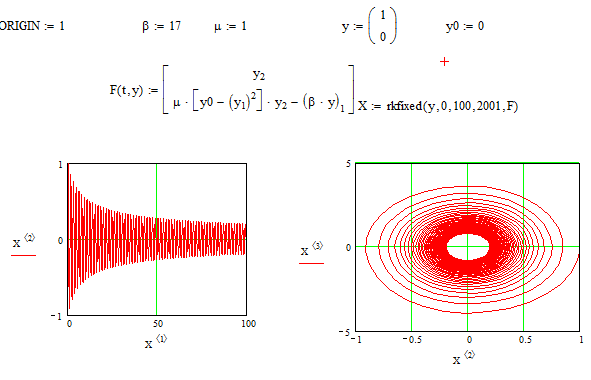
Рис. 3.27 - Программа осциллятора Ван-дер-Поля при β=17, μ=1, y0=0
При β=17, μ=-1, y0=1 (рис. 3.28).
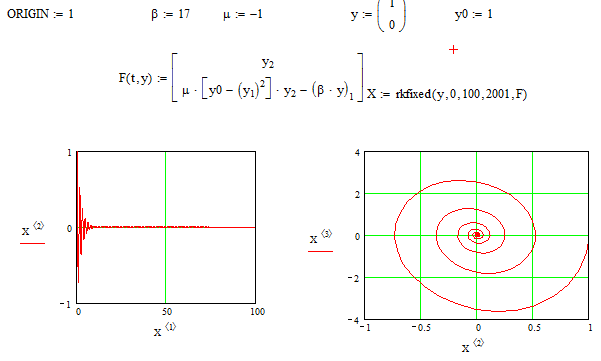
Рис. 3.28 - Программа осциллятора Ван-дер-Поля при β=17, μ=-1, y0=1
При β=17, μ=10, y0=1 (рис. 3.29).
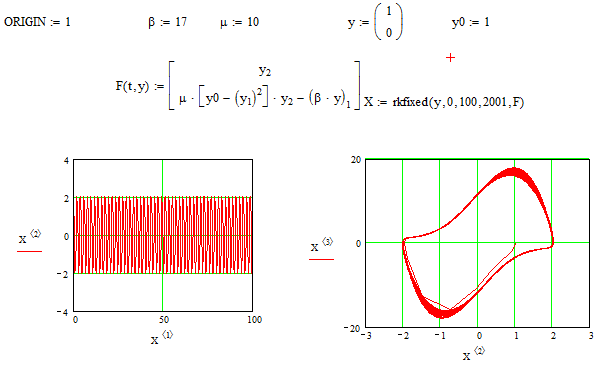
Рис. 3.29 - Программа осциллятора Ван-дер-Поля при β=17, μ=10, y0=1
При β=17, μ=10, y0=0 (рис. 3.30).
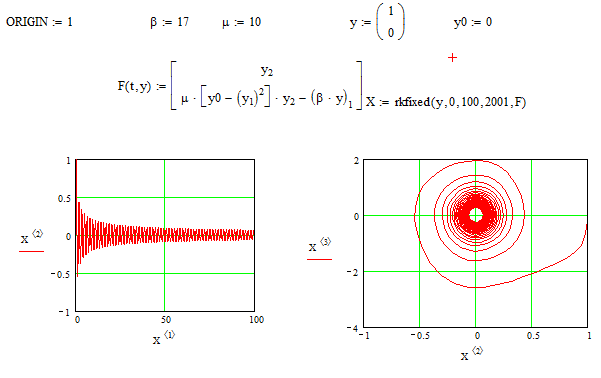
Рис. 3.30 - Программа осциллятора Ван-дер-Поля при β=17, μ=10, y0=0
Выводы:
Результаты исследования внести в таблицу 3.4.
Таблица 3.4 – Результаты исследования
|
β |
μ |
y0 |
Тип колебания |
|
17 |
1 |
1 |
Установившиеся гармонические |
|
17 |
1 |
-1 |
Затухающие гармонические |
|
17 |
1 |
10 |
Установившиеся релаксационные |
|
17 |
1 |
0 |
Затухающие гармонические |
|
17 |
-1 |
1 |
Затухающие гармонические |
|
17 |
10 |
1 |
Установившиеся релаксационные |
|
17 |
10 |
0 |
Затухающие гармонические |
Установившиеся релаксационные колебания возникают при μ=1 y0=10 и при μ=10 y0=1. Затухающие гармонические колебания возникают при μ=1 y0=-1, μ=1 y0=0, μ=-1 y0=1, μ=10 y0=0. При остальных значениях β, μ, y0 колебания отсутствуют.
3.4 Лабораторная работа «Параметрические колебания»
Рассмотрена лабораторная работа «Исследование параметрического усилителя».
Цель работы: изучение параметрического усиления.
Заданные значения элементов: R1=10Ohm, L1=50μH, E=10V, D1 - № варианта.
3.4.1 Лабораторная работа «Исследование параметрического усилителя»
Собрать схему параметрического усилителя, состоящую из R1-сопротивление, L1-индуктивность, D1 - варикап (рис. 3.31).
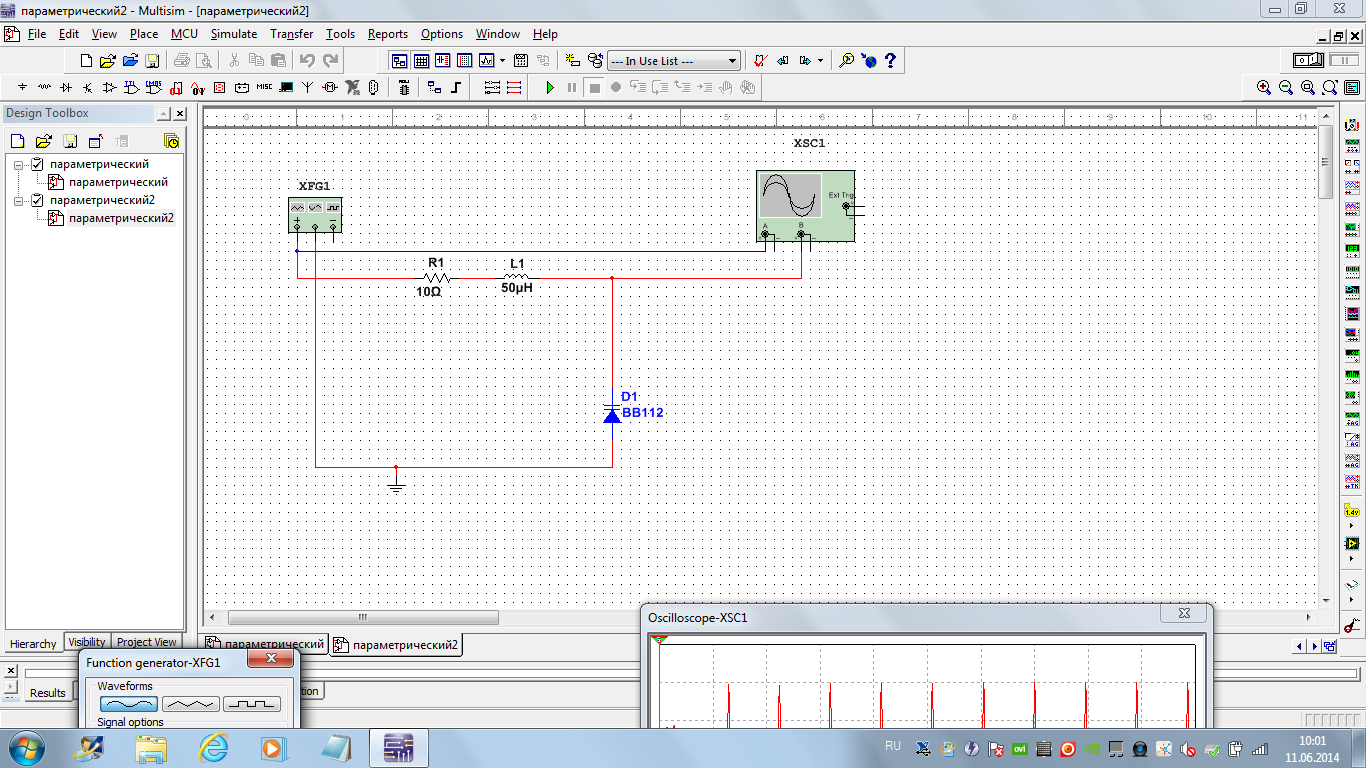
Рис. 3.31 – Схема параметрического усилителя
На вход подать синусоидальный сигнал и с помощью осциллографа найти частоту, в котором происходит максимальное усиление сигнала(рис. 3.32).
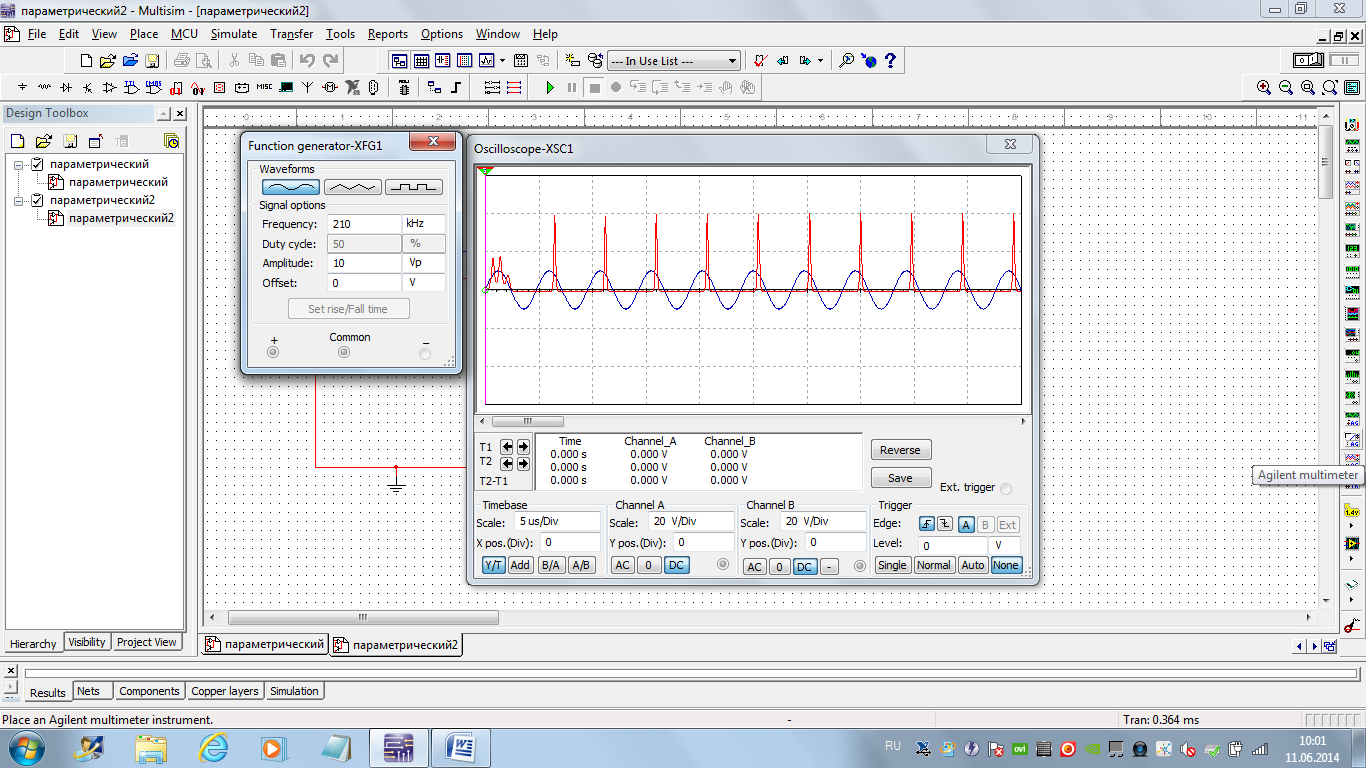
Рис. 3.32 – Осциллограмма входного и выходного сигнала
Вывод:
При подаче синусоидального сигнала с частотой, в котором происходит максимальное усиление сигнала, выходной сигнал имеет вид импульсов.
3.5 Лабораторная работа «Нелинейные волны»
Приведена лабораторная работа «Солитоны».
3.5.1 Лабораторная работа «Солитоны»
Цель работы: изучение солитонов на эквивалентной схеме линии передачи.
Заданные значения элементов: L1-L60=23μH, C1-C60=100pF, C61=10μF, E=10V.
Собрать эквивалентную схему, состоящую из 60 ячеек, включающих L1-L60 –катушки индуктивности, C1-C60 – ёмкости, C61 – ёмкость для сглаживания ВЧ пульсаций, D1-D60 – варикапы, R1 – сопротивление (рис.3.33).
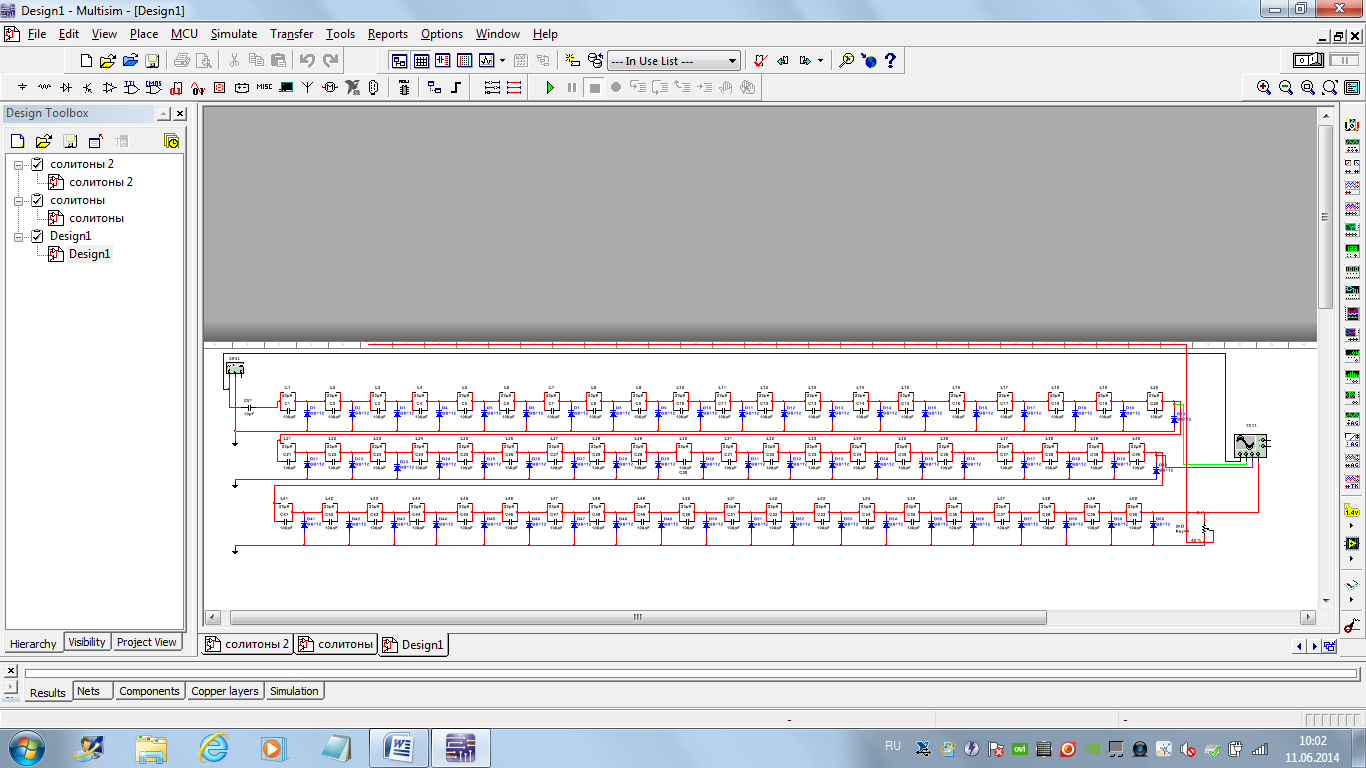
Рис. 3.33 – Эквивалентная схема исследуемой линии передачи
На вход подать прямоугольный сигнал и с помощью осциллографа найти частоту и длительность цикла, в котором наблюдаются солитоны (рис. 3.34)
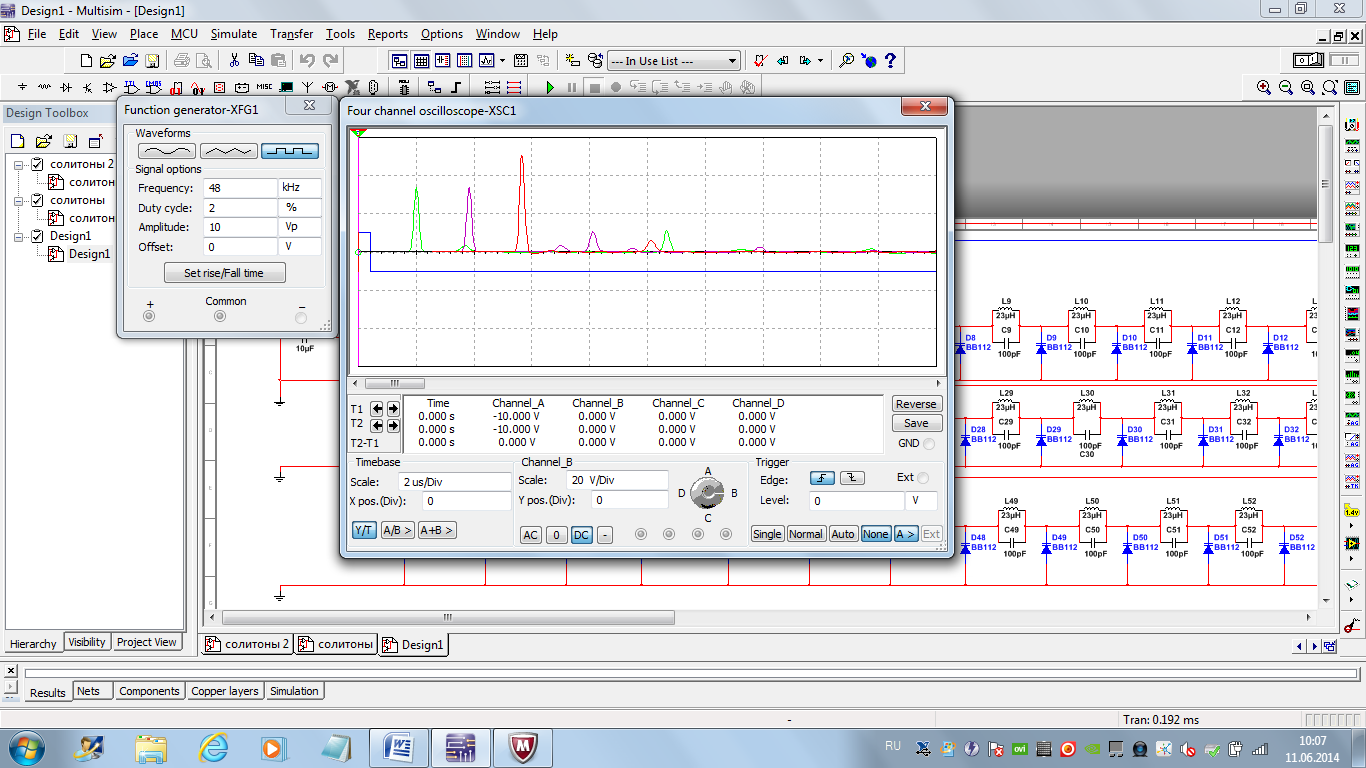
Рис. 3.34 – Осциллограмма: входной прямоугольный сигнал, сигнал на выходе 20 ячейки, сигнал на выходе 40 ячейки, сигнал на выходе 60 ячейки
Выводы:
При подаче прямоугольного сигнала на выходах 20, 40, 60 ячеек образуются солитоны с разными амплитудами. Длительность колебаний одинаковая.