Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ИДЗ по матем II семестр ФЭУ

.pdf

Скачиваний:

Добавлен:

03.05.2015

Размер:

224.39 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Индивидуальные задания

по математике

Дифференциальные уравнения

1. Найти общее решение дифференциального уравнения.

1.1. sec2 x tg y dx + sec2 y tg x dy = 0;

(

)

(

)

(

)

1.2.

+1 dx +

−1

y −1 dy = 0;

(

)

−

(

)

= 0;

1.3.

y +1 dx

x2 +1 dy

1.4.

y (1+ x2 )dy − x(1+ y2 )dx = 0;

1.5.

xy (1+ y2 )dx − (1+ x2 )dy = 0;

1.6.

1+ y2 + y

1+ x2 y′ = 0;

1.7.

(4 − x2 )cos y dy + 4sin y dx = 0;

1.8.

tg xsin2 y dx + cos2 xctg y dy = 0;

1.9.

sin x(cos y)−1 dx + esin y (cos x)−2 dy = 0;

1.10.

2xsin y dx − (1+ x2 )dy = 0;

1.11.

(x2 −1) y′ + 2xy2

= 0;

(

)(

)

−1

1.12.

y′ = 1+ y

1+ x

;

1.13.

1− y2 dx + y 1− x2 dy = 0;

1.14.

3ex tg y dx + (1− ex )sec2 y dy = 0;

1.15.

dy + y ctg x dx = 0;

1.16.

y′ =10x+y;

1.17.

y y′ = (1− 2x)

1.18.

1− y22

+ y′ = 0;

1−x

1.19.ex−y y′ =1;

1.20.y′ = y2 x−1 ( y −1)−1 ;

1.21.(xy2 + x)dx + (y − x2 y)dy = 0;

1.22.3ey tg x dy + (1− ey )sec2 x dx = 0;

1.23.sin x(cos y)−1 dx + esin y cos2 x dy = 0;

1.24.sin x sin y dx + cos x cos y dy = 0.

2.Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию.

2.1.

2(yy′x2 − xy2 )

= x3 exp{−(

)2 }; y(1) = 0;

2.2.

x2 y′ = y2 − xy;

y(1) = 2;

2.3.

ey x (x y′ − y) = x;

y(1) = 0;

2.4.

y − xy′ = xsin2

;

y(1) = π 2;

2.5.

y′ = (x2 + xy + y2 )x−2;

y(1) = 0;

2.6.

xy′ = y(1+ ln

);

y(1) = 2;

2.7.

y′ = ey x +

;

y(1) = 1;

2.8.

2x2 y′ = x2 + y2 ;

y(1) = 0;

2.9.

y − x y′ = xsin

;

y(1) = π 2;

2.10.

y2 + x2 y′ = x y y′;

y(1) = 1;

2.11.

xy′ − y = (x + y)ln

x+ y

;

y(1) = 1;

2.12.

y′ = y2 (xy − x2 )−1 ;

y(1) = 1;

2.13.

(y2 − x2 ) y′ + xy = y2 ;

y (1) = 1;

dx; y(1) = 1;

2.14.

xdy − ydx =

y2 − x2

2.15.

(x − y) dy = ydx;

y(1) = 1;

2.16.

y′ =

; y(1) = 1;

2.17.

y′ = (x + y)(x − y)−1 ;

y (1) = 0;

y(1) = 0;

2.18.

xy′ = y +

x2 + y2 ;

2.19.

xy′ = y ln

;

y(1) = 1;

2.20.

xy′ = y(1+ ln

);

y(1) = e−1 2 ;

2.21.

xy′ cos

= y cos

− x;

y(1) = π 2;

y (1) = 0;

2.22.

y′ =

x2 + y2

2.23.

y′ = sin

;

y(1) = π 2;

2.24.

y′ = x2 y2 + y

y(1) = 0.

3. Найти общее решение дифференциального уравнения.

3.1.

y sin x + y′ cos x = 1;

3.6.

y′ +

= 3x2 ;

3.2.

2xy′ − 6y + x2 = 0;

3.7.

−3x

;

3.3.

y′ + y tgx = sin 2x;

y′ + 3y = x

3.8.

y′ + y tgx = cos2 x;

3.4.

y′ + y cos x = cos x;

3.9.

y′ + y = cos x;

3.5.

y′ + y ctgx = 4 sin x;

3.10.

2y′ − 2y tg x = 3x;

3.11.	y′ +	3	y = x2e3 x ;	3.18.	y′ + y = x + 2;
		x2
3.12.	y′ + y = sin x;			3.19.	y′ + xy = xe− x2 ;
3.13.	y′ +	3	y = 1 x2 ;	3.20.	xy′ − 2y = 4x4 ;
		2
		x			x( y′ − y) = ex ;
3.14.	y′ cos x + y sin x = 1;			3.21.
3.15.	y′ + y − x2 = 0;			3.22.	xy′ + y = ex;
3.16.	y′ + xy = exp{− x2 2};			3.23.	y = x( y′ − x cos x);
3.17.	y′ cos x − ysin x = cos2 x;			3.24.	xy′ = x3 − y.

4.Для дифференциального уравнения найти интегральную кривую, проходящую через точку M0(x0, y0).

y′ − y cos x = 2

cos x;

M0 (0, 4);

4.1.

4.2.

y′ + y cos x = y2 cos x;

M0 (0,1);

4.3.

y′ +

= x2 y3;

M0 (1,1);

4.4.

y′ + y tg x = y2 sin x;

M0 (0,1);

4.5.

y′ − xy (1− x2 )−1 = xy2 ;

M0 (0,1);

4.6.

xy′ = − y − xy2 ;

M0 (1,1);

4.7.

xy′ + y = xy2 ln x; M0 (1,1);

4.8.

ydy = (y2 x2 − x3 )dx;

M0 (1,1);

4.9.

xy′ + y = y2 ;

M0 (1, 2);

4.10.

y′ + y tgx = y3

cos x;

M0 (0,1);

y′ + y x =

M0 (4, 0);

4.11.

y′ + y sin2 x = 2

sin2 x; M0 (π 2, 4;)

4.12.

y′ −

y = 2

e−1 x ;

(1, e−2 );

4.13.

4.14.

2x y y′ = y2 − x;

M0 (1,1);

4.15.

y′ = y4 cos x + y tgx;

M0 (0, −1);

4.16.

y′ + 2xy = 2x3 y3;

M0 (0,1);

4.17.

y′ = y x +1

M0 (1, 0);

4.18.

y′ − xy = − y3 exp

{−x3 };

M0 (0,1);

4.19.

y′ + y x = −xy2 ;

M0 (1, 2);

4.20.

y′ = xy + x3 y3;

M0 (0,1);

y′ + yctgx =

;

M0 (π 2, 0);

4.21.

y sin x

4.22.

(1− x2 )dy − xydx = xy2dx;

M0 (0, −1);

4.23.

2xyy′ = y2 − x2 ;

M0 (0,1);

4.24.

xy′ = 3y − x4 y2 ;

M0 (1,1).

5. Найти общее решение дифференциального уравнения.

5.1.y′′ = sin2 x;

5.2.y′′ = cos2 x;

5.3.y′′ =1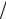sin2 x;

5.4.y′′ =1cos2 x;

5.5.y′′ = x + sin x;

5.6.y′′ = x2 + cos x;

5.7.y′′ = ln x;

5.8.y′′ = arctg x;

5.9.y′′ = (x +1)−2 ;

5.10.y′′ = (x +1)−3 ;

5.11.y′′ =1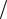x2 −1x;

5.12.y′′ = (x2 + 2)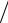(x2 +1);

5.13.y′′ = x;

5.14.y′′ = 2x;

5.15.y′′ = cos2 2x ;

5.16.y′′ = tg2 x;

5.17.y′′ = ctg2 x;

5.18.y′′ = 1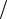(x − 2);

5.19.y′′ = 1(3 − x);

5.20.y′′ = cos x − cos 2x;

5.21.y′′ = sin (2x − 3);

5.22.y′′ = sin2 x2 ;

5.23.y′′ = 1cos2 x2 ;

5.24.y′′ = 1sin2 x2 .

6. Найти общее решение дифференциального уравнения.

6.1.y′′ + y′ctg x = 3cos x;

6.2.xy′′ = y′ + x2;

6.3.y′′ − 3 y′x = 2x3;

6.4.y′′ sin x = y′ cos x;

6.5.y′′ = y′x + x;

6.6.(x +1) y′′ − (x + 2) y′ = −x − 2;

6.7.xy′′ = y′;

6.8.y′′ + y′tg x = sin 2x;

6.9.xy′′ − y′ + x = 0;

6.10.x2 y′′ = ( y′)2 ;

6.11.y′′ (x2 +1) = 2xy′;

6.12.y′′ + 2x( y′)2 = 0;

6.13.xy′′ − y′ = ex x2;

6.14.xy′′ = y′ ln( y′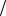x);

6.15.x3 y′′ + x2 y′ =1;

6.16.y′′x ln x = y′;

6.17.2xy′′ = y′;

6.18.y′′ − y′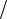(x −1) = x(x −1);

6.19.y′′ = y′ + x;

6.20.2xy′y′′ = ( y′)2 +1;

6.21.y′′ − 2y′ctg x = sin3 x;

6.22.y′′ = y′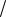x + x3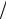y′;

6.23.y′′ = y′ ln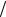 xx;

6.24.(1+ x2 ) y′′ = 1+ ( y′)2 .

7.Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям.

7.1.	2yy′′ = ( y′)2 +1; x = 1, y = 1, y′ = 0;

7.2.6yy′′ = 2 + 3( y′)2 ; x = 0, y = 25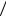12, y′ = 16;

7.3.y′′ = 1 y ; x = 0, y = 1, y′ = 2;

7.4.y3 y′′ = −1; x =1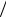2, y =1, y′ =1;

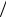7.5.3y′′ = 4y5; x = −34, y =1, y′ = 23;

7.6.	3y y′′ + 4y′ = 3( y′)2 ;	x = 0, y = −3, y′ = 1 3;
7.7.	4yy′′ = 4( y′)2 − 3y′;	x = 0, y = −2, y′ = 1 4;
		4

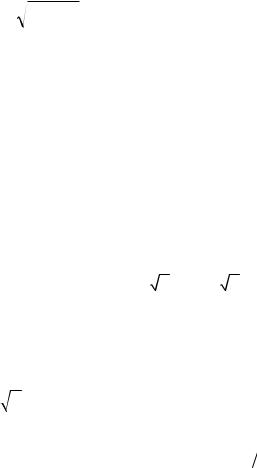
7.8.y′′ = 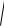1+ ( y′)2 ; x = 0, y = 1, y′ = 0;

7.9.yy′′ = ( y′)2 ; x = 0, y = 1, y′ = 1;

7.10. y′′ + 2( y′)2 (1− y) = 0; x = −1, y = 2, y′ = 1;

7.11.( y′′)2 = y′; x = 2, y = 2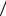3, y′ = 1;

7.12.yy′′ + ( y′)2 = 1; x = 0, y = 1, y′ = 1;

7.13.2y ( y′)3 + y′′ = 0; x = 0, y = 0, y′ = −3;

7.14.2y′′ = 3y2; x = −2, y =1, y′ = −1;

7.15. yy′′ = ( y′)2 − ( y′)3 ; x = 1, y = 1, y′ = −1;

7.16.y′′ = e2 y; x = 0, y = 0, y′ =1;

7.17.y3 y′′ = y4 −1; x = 0, y = 2; y′ = 12 ;

7.18. y′′( y −1) = 2( y′)2 ; x = 1, y = 2, y′ = −1;

7.19.y3 y′′ =1; x = −2, y =1, y′ = −1;

7.20.2yy′′ = ( y′)2 ; x = −1, y = 4, y′ = 1;

7.21.y′′ y = 14; x = 43, y = 1, y′ = 1;

7.22.y′′y′ = y2; x = −1, y =1, y′ =1;

7.23.	3yy′′ = 3( y′)2 − 4y′; x = 0, y = −3, y′ = 1 3;
7.24.	( y′′)2 − ( y′)2 = 1; x = 0, y = 1, y′ = 0.

Линейная алгебра

8. Вычислить определитель.

	1	1	0	3
8.1.	0	1	1	2	;
8.1.	2	1	2	1	;
	1	0	3	1
	1	1	1	4
	1	1	1	4
8.2.	1	1	2	1	;
8.2.	1	2	1	1	;
	4	1	1	1
	3	4		6	7
	3	4		6	7
8.3.	1	−2		3	4		;
8.3.	5	−1		2	4		;
	8	7		1	5
	1	1	4	1
	1	1	4	1
8.4.	2	1	3	0	;
8.4.	3	1	2	1	;
	4	1	1	0
	1	2	6	7
	1	2	6	7
8.5.	2	2	3	4	;
8.5.	3	3	3	4	;
	4	4	4	4
	3	1	1	1
	3	1	1	1
8.6.	1	2	1	1	;
	1	1	2	1
	1	1	1	3
	1	1		1	1
	1	1		1	1
8.7.	1	2		3	4		;
8.7.	1	4		10	20		;
	1	3		6	10
	1	2	3	4
	1	2	3	4
8.8.	2	3	4	1	;
	3	4	1	2
	4	1	2	3
	1	1		1	1
	1	1		1	1
8.9.	1	2		3	4		;
8.9.	1	4		9	16		;
	1	8		27	64
	1	2		3	4
	1	2		3	4
8.10.	−2	1 −4			3	;
8.10.	3 −4		−1		2	;
	4	3 −2 −1

	2	1	3	1
8.11.	4	3	7	3		;
8.11.	1	7	8	7		;
	3	9	12	6
	1	3	−1		1
	1	3	−1		1
8.12.	1	2	3	−1			;
8.12.	3	0	−1		1		;
	1	1	4	5
	2	1 −1		0
	2	1 −1		0
8.13.	3	5	4 −1		;
8.13.	0	2	1	3	;
	1 −1		3	1
	1	2	3 −1
	1	2	3 −1
8.14.	1	1 −1		1	;
8.14.	3	0	−1	2	;
	0	1	4 −1
	1	2	3	1
	1	2	3	1
8.15.	3	0 −1 −1			;
8.15.	7	1	1	3	;
	4	1	4 −1
	1	1	3 −1
	1	1	3 −1
8.16.	1	0 −1		1	;
8.16.	3	7	−1	1	;
	0	4	4 −1
	1	2	1 −1
	1	2	1 −1
8.17.	1	5	4	1	;
	3	0	7	1
	1	1	3	1
	2	1	3	0
	2	1	3	0
8.18.	3	5	4 −1		;
8.18.	0	2	1	3	;
	1 −1		4	4
	2	1	4	2
	2	1	4	2
8.19.	3	5	4 −1		;
8.19.	0	2	1	3	;
	3 −1		3	1
	2	1 −1		0
	2	1 −1		0
8.20.	2	3	2	3	;
8.20.	0	2	1	3	;
	1 −1		6	1

	2	-5	1	2
	2	-5	1	2
8.21.	3	5	4	-1		;
8.21.	0	2	1	3		;
	1 -6		3	1
	2	1	-1	1
	2	1	-1	1
8.22.	3	5	4	-1		;
8.22.	0	2	1	3		;
	5	-1	3 -9
	2	1 -1		0
	2	1 -1		0
8.23.	3	3	4 -1		;
8.23.	1	2	1	3	;
	1	-1	3	1

9.Найти значение полинома f(x) от матрицы A.

9.1. f (x) = 3x2 - 2x + 5,

æ	1 −2		3ö
A = ç	2	−4	1÷ ;
è	3	−5	2ø

9.2. f (x) = x3 - 7x2 - 2x + 5,

æ	5	2	−3ö
A = ç	1	3 −1÷ ;
è	2	2	−1ø

9.3.f (x) = x3 - x2 - 9x + 9,

æ 1 2 −2ö

=ç 1 0 3÷ ;

è 1 3 0øA

9.4.f (x) = x3 - 5x2 + 7x - 3,

æ 1 −2 0ö

=ç −2 1 0÷ ;

è 0 0 3øA

9.5. f (x) = 4x4 -10x3 + 3x2 ,

æ0 1 0ö

A = ç0 0 1÷ ;

è0 0 0ø

9.6. f (x) = x2 - 3x - 9,

æ	5	2	−3ö
A = ç	1	3	−1÷ ;
è	2	1 −1ø

	2	-2	-1	1
	2	-2	-1	1
8.24.	3	5	4	-1	.
8.24.	0	2	1	4	.
	1 -1		3	1

9.7. f (x) = x2 - 2x + 3,

æ 1 0 0ö

A = ç 0 1 2÷ ;

è 4 3 5ø

9.8. f (x) = 3x2 - x + 4,

æ	1 −1		2ö
A = ç	3	0	1÷ ;
è	0	2 −1ø
9.9. f (x) = (x -1)2 ,
æ	3	2	−1ö
A = ç	1	1	5÷ ;
è	2 −3		1ø

9.10. f (x) = (2x - 2)3 ,

æ	3	0	0ö
A = ç	−1	2	2÷ ;
è	0	1	1ø
9.11. f (x) = 2x3 + 3,
æ −1		2	1ö
A = ç	1	0	3÷ ;
è	2 −1		1ø

9.12. f (x) = x3 - x2 + 4,

æ	1	2	0ö
A = ç	−1	1	0÷ ;
è	2	0	−1ø

9.13.f (x) = x3 - 2x + 4,

æ	0	1	1ö
A = ç	−1	1	−3÷ ;
è	1	−1	0ø

9.14. f (x) = x3 - x + 5,

æ	1	0	0ö
A = ç	2	−1	0÷ ;
è	0	1	2ø

9.15. f (x) = 2x2 + x + 3,

æ	4	−2	0ö
A = ç	0	3 −1÷ ;
è	1	1	1ø

9.16.f (x) = 2x2 - x - 3,

æ 0 −1 1ö

=ç 1 −1 0÷ ;

è 0 2 −1øA

9.17.f (x) = x3 + 2x2 -1,

æ	1	2	0ö
A = ç	0	0	2÷ ;
è	1	2	−1ø

9.18. f (x) = x3 - 3x + 4,

æ	1	2	−1ö
A = ç	0	0	1÷ ;
è	2	−1	0ø

9.19.f (x) = x3 + 6x2 - 2x + 3,

	æ −1		0	1ö
	A = ç	0	1	1÷ ;
	è	1	1 −1ø
9.20.	f (x) = 3x2 + x -1,
	æ	1	0	1ö
	A = ç	−1	3	1÷ ;
	è	1	1	1ø
9.21.	f (x) = 2x2 + 3x +1,
	æ	1	0 −1ö
	A = ç	1	1	0÷ ;
	è −1		2	1ø
9.22.	f (x) = 3x2 + x -1,
	æ	1	2	−1ö
	A = ç	0	1 −2÷ ;
	è	2	1	0ø
9.23.	f (x) = (x + 2)3 ,
	æ	1	0	2ö
	A = ç	0	−2	1÷ ;
	è	1	1 −1ø
9.24.	f (x) = (3x +1)2 ,
	æ	1	−1	1ö
	A = ç	1	0	1÷ .
	è	0	2 −1ø

10.Найти матрицы, обратные данным; проверить правильность вычислений, перемножив взаимно обратные матрицы.

A = (

23 −−21),

æ 1 1 0ö

A = (45 33),

1 2 2ö

10.1.

B = ç 2 3 1÷ ;

10.5.

B = ç

1 −2÷ ;

è 4 1 0ø

è 2 −2 1ø

A = (31

42),

7ö

A = (−−21

æ 1

1 3ö

10.2.

B = ç

4÷ ;

10.6.

45), B = ç 0 0

1÷ ;

è 5 −2 −3ø

è 3 4 1ø

A = (53

77),

æ 3 −4

5ö

A = (−6Ѕ

04),

æ 2 1 5ö

10.3.

B = ç

−3

1÷ ;

10.7.

B = ç 3 2 0÷ ;

è 3 −5

−1ø

è 0 0 1ø

A = (−23 41),

æ 2 7

3ö

A = (53 12),

1ö

10.4.

B = ç 3 9

4÷ ;

10.8.

B = ç

1÷ ;

è 1 5 3ø

è 0

1 −1ø

			æ −2		1	0ö
10.9.	A = (13 79), B = ç			3	1	1÷ ;
			è	1	2	−1ø
	A = (43	22),	æ 2		1	1ö
10.10.	A = (43	22),	B = ç 3		0	1÷ ;
			è 0		1	4ø
	A = (24 −11),		æ		1	3	1ö
10.11.	A = (24 −11),		B = ç		4	1	1÷ ;
			è −5 −4 −1ø
	A = (−31 −21),		B =	æ	5	3 −1ö
10.12.	A = (−31 −21),		B =	ç	0	1	2÷ ;
				è −1		1	0ø
	A = (−72 −11),		B =	æ	1 −2		3ö
10.13.	A = (−72 −11),		B =	ç	3	−1	0÷ ;
				è	0	4	2ø
	A = (42	53),	æ9		7	6ö
10.14.	A = (42	53),	B = ç 1		1	2÷ ;
			è 1		1	1ø
	A = (−05	21),	B =	æ	1	3 −2ö
10.15.	A = (−05	21),	B =	ç	2	−1	1÷ ;
				è	3	2	0ø
	A = (−71 −−21),		B =	æ	1 −1		2ö
10.16.	A = (−71 −−21),		B =	ç	2	4 −1÷ ;
				è	4	2	0ø

	A = (	21 −21),				æ	5	−6	4ö
10.17.	A = (	21 −21),			B = ç		3	−3	2÷ ;
						è	4	−5	2ø
	A = (	21 −63),				æ −1 −1			2ö
10.18.	A = (	21 −63),			B = ç		0	5 −3÷ ;
						è −1		4	0ø
	A = (	31 −42),				æ	2	3	1ö
10.19.	A = (	31 −42),			B = ç		4 −1		1÷ ;
						è	5	1	1ø
	A = (	−11	01),			æ	4	−3	2ö
10.20.	A = (	−11	01),		B = ç		6	−2	3÷ ;
						è	5	−3	2ø
	A = (	−11	72),			æ	5	−6	4ö
10.21.	A = (	−11	72),		B = ç		3	−3	2÷ ;
						è	4	−5	2ø
	A = (	12 13),			æ	4	5	1ö
10.22.	A = (	12 13),		B = ç		3	4	0÷ ;
					è	1	1 −1ø
	A = (	51	−23),			æ 2 3 5ö
10.23.	A = (	51	−23),		B = ç 3 7			4÷ ;
						è 1 2 2ø
	A = (11 01),				æ	2	1 −1ö
10.24.	A = (11 01),			B = ç		1	2	1÷ .
					è	1 −2		0ø

11.Методом Гаусса найти общее решение и какое-нибудь частное решение (если таковые существуют).

ì3x + 2x

+ x

+ x - 3x

= -2,

ì2x

- x

+ x

= 1,

11.1.

+ 2x3

+ 2x4

+ 6x5

= 23,

11.5.

ï8x1

+ 12x2

- 9x3

+ 8x4

= 3,

= 7,

í4x1

6x2

+ 3x3

- 2x4

= 3,

î5x1

4x2

3x3

3x4

= 12;

î2x1

3x2

+ 9x3

- 7x4

= 3;

ì3x

+ 2x

+ 5x

+ 4x

= 3,

ì2x

- x - x + 3x = 1,

11.6.

ï2x11

+ 3x22

+ 6x33

+ 8x44

= 5,

- 6x2

- 9x3

- 20x4

= -11,

11.2.

ï4x1

2x2

í6x

- 3x

î4x1

+ 4x3

ï2x1

+ 2x3

- 12x4

= 10;

ì2x

- x + 5x - 6x

= 1,

ì 2x

- x

+ 3x - 2x

= 4,

11.3.

ï2x1

- x2

- 3x3

+ 4x4

= 5,

11.7.

4x1

- 2x2

+ 5x3

+ x4

= 7,

í2x1

= 3,

2x1

- x2

+ 8x4

= 2,

î4x1

2x2

2x3

3x4

= 2;

î14x1

- 7x2

+ 22x3

- 19x4

= 29;

ì2x

+ 7x

+ 3x + x

= 5,

11.4.

x11

+ 3x22

+ 5x33

- 2x44

= 3,

ì2x - 3x + 5x + 7x = 1,

+ 5x2

- 9x3

+ 8x4

= 1,

= 2,

11.8.

ï4x1

6x2

+ 2x3

3x4

î5x1

+ 18x2

+ 4x3

+ 5x4

= 12;

í2x

- 3x

- 11x

- 15x

= 1,

ï6x1

- 9x2

- x3

- x4

= 3;

	ì3x + 3x - 2x						- 4x	= 1,
11.9.	ï2x1		- x2		+ 3x3		- 4x4	= 3,
	í	x1	- 14x2		+ 21x3		- 8x4	= 12,
	ï9x1		+ 18x2		- 19x3		- 8x4	= -1;
	î	1		2		3	4
	ì3x		- 2x	+ 5x		+ 4x		= 2,
11.10.	ï6x1		- 4x2	+ 4x3		+ 3x4		= 3,
	í9x1		- 6x2	+ 3x3		+ 2x4		= 4,
	ï3x1		- 2x2	- 13x3		- 11x4		= -1;
	î	1	2		3		4

ì3x + 4x + x + 2x = 3,

= 7,

11.11.

í6x1

+ 8x2

+ 2x3

5x4

ï9x

+ 12x

+ 3x

+ 10x

= 13;

ì5x - 5x + 8x - 7x = 3,

= 2,

11.12.

- x2

2x3

- x

+ x

- 2x

= 1;

ì5x

- 3x

+ 2x

+ 4x

= 3,

11.13.

ï4x1

- 2x2

+ 3x3

+ 7x4

= 1,

í8x1

- 6x2

5x4

= 9,

ï7x1

- 3x2

+ 7x3

+ 17x4

= 0;

ì2x + x - x - x + x

= 1,

11.14.

- x2

+ x3

+ x4

- 2x5

= 0,

3x1

+ 3x2

- 3x3

- 3x4

+ 4x5

= 2,

ï4x1

+ 5x2

- 5x3

- 5x4

+ 7x5

= 3;

ì2x - 3x + 5x + 7x = 1,

= 2,

11.15.

í4x1

- 6x2

2x3

3x4

ï2x

- 3x

- 11x

- 15x

= 1;

ì3x - 2x + 5x + 4x = 2,

= 3,

11.16.

í6x1

- 4x2

4x3

+ 3x4

ï9x

- 6x

+ 3x

+ 2x

= 4;

ì2x

- x

+ x

+ 2x

+ 3x

= 2,

11.17.

ï6x1

- 3x2

+ 2x3

+ 4x4

+ 5x5

= 3,

í6x1

- 3x2

+ 4x3

+ 8x4

+ 13x5

= 9,

ï4x1

- 2x2

+ x3

+ x4

+ 2x5

= 1;

	ì6x		+ 4x	+ 5x	+ 2x	+ 3x	= 1,
11.18.	ï3x1		+ 2x2	+ 4x3	+ x4	+ 2x5	= 3,
11.18.	í3x1		+ 2x2	- 2x3	+ x4	5	= -7,
	ï9x1		+ 6x2	+ x3	+ 3x4	+ 2x	= 2;
	î	1	2	3	4	5
	ì8x		+ 5x	- 10x - 3x		= 37,
11.19.	ï	x1	+ 5x2	+ 3x3	+ 2x4	= 13,
11.19.	í	x1	+ x2	3	4	= 5,
	ï	1	2	- 2x3 + x4 = -2;
	î3x1		- 2x2	- 2x3 + x4 = -2;

ì 8x1 - x2 - x3 + 3x4 = 30,

11.20.ïí 5x1 - 5x2 - x3 - 2x4 = 1,

ï10x1 + 3x2 + 2x4 = 51, î 3x1 + 2x2 + x4 = 19;

	ì3x		+ x	+ 2x		+		2x	= 27,
11.21.	ï4x1		+ 3x2			-		x4	= 50,
	í9x1		+ 7x2	- 6x3		+ 17x4			= 93,
	ï2x1		+ 2x2	- 7x3		+		7x4	= 12;
	î	1	2		3			4
	ì5x		+ 5x	+	7x		-	4x		= -19,
11.22.	ï5x1		+ 6x2	+ 24x3			- 14x4			= -74,
	í2x1		+ 4x2	+	x3				4	= -17,
	ï	1	2		3		+ 2x4
	î		x2	-	3x3					= 1;

ì 2x1 - 4x2 + 2x3 + x4 = -23,

11.23.ïí10x1 - 9x2 + 7x3 - 5x4 = -37, ï 10x2 + 2x4 = 96, î 4x1 + 3x2 + = 62;x3

	ì5x		+ 3x	+	x	-	x	=	37,
11.24.	ï5x1		2	+ 18x3		+ 2x4		= 122,
11.24.	í6x1		+ 2x	+	5x3	+	x4	=	64,
	ï2x1		+ x2	+	3x3		4	=	28.
	î	1	2		3

12. Методом Гаусса решить систему однородных уравнений.

ì x

+ 2x

+ 4x

- 3x

= 0,

ì5x

+ 6x

- 2x

+ 7x

+ 4x

= 0,

12.1.

3x1

+ 5x2

+ 6x3

- 4x4

= 0,

12.3.

ï2x1

+ 3x2

- x3

+ 4x4

+ 2x5

= 0,

í4x1

+ 5x2

- 2x3

+ 3x4

= 0,

í7x1

+ 9x2

- 3x3

+ 5x4

+ 6x5

= 0,

3x1

+ 8x2

+ 24x3

- 19x4

= 0;

ï5x1

+ 9x2

- 3x3

+ x4

+ 6x5

= 0;

ì3x

+ 2x

+ x

+ 3x

+ 5x

= 0,

12.2.

ï6x11

+ 4x22

+ 3x33

+ 5x44

+ 7x55

= 0,

+ 4x

+ x

+ 2x

+ 3x = 0,

+ 6x2

+ 5x3

+ 7x4

+ 9x5

= 0,

ï9x1

12.4.

ï5x1

7x2

3x4

+ 4x5

î3x1

+ 2x2

+ 4x4

+ 8x5

= 0;

í4x

+ 2x

+ 5x

= 0,

ï7x1

+ 10x2

+ x3

+ 6x4

+ 5x5

= 0;

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.2015953.54 Кб70ИДЗ Мех поступ и вращат движения. сент.2014-1.docx
#
29.03.20151.01 Mб204ИДЗ Мех поступ и вращат движения.docx
#
13.03.2016618.64 Кб123ИДЗ МКТ и ТД - сентябрь 2015.docx
#
09.09.2019483.84 Кб1ИДЗ Мт-201.doc
#
23.02.20152.64 Mб23ИДЗ по матану.pdf
#
03.05.2015224.39 Кб8ИДЗ по матем II семестр ФЭУ.pdf
#
22.02.2015949.62 Кб74ИДЗ № 1.docx
#
22.02.2015405.58 Кб142ИДЗ № 2.docx
#
18.09.20191.74 Mб20ИДЗ(теор.вер)рабоч.doc
#
22.02.201573.22 Кб15ИДЗ-ДУ.doc
#
22.02.2015218.11 Кб97ИДЗ-Механика-1.doc