
Nedelko_Sport_metrolog
.pdf
Генеральноесреднеесвероятностью0,95 покрываетсяинтервалом
(61,6; 63,4).
2.СРАВНЕНИЕСРЕДНИХПОКРИТЕРИЮСТЬЮДЕНТА
Впрактикетренерачастоприходитсясталкиватьсясосравнением среднихрезультатовдвухгруппспортсменов. Этосравнениеимеетцельюотделитьвлияниенарезультатсущественногофактора(уровняпрофессиональнойготовностиспортсменакучастиювсоревнованиях) от неизбежного присутствия элемента случайности. Рассмотрим три варианта:
сравнениедвухбольшихгрупп(n > 30) илиоднойбольшойиодной
малойгруппы(n ≤ 30) спопарнонезависимымизначениями; сравнениедвухмалыхгруппспопарнонезависимымизначениями; сравнениедвухмалыхгруппспопарнозависимымизначениями. Схема сравнения средних предполагает вычисление в каждом из
указанных случаев наблюдаемого значения критерия Стьюдента tнабл и сопоставлениеегоскритическимзначениемtкр, определяемымпотаблице(приложение4), гдеприведенызначенияtкр длятрехуровнейдоверительнойвероятностиγ = 0,95; 0,99; 0,999. Приэтомвозможныследующиеслучаисоотношенияtнабл иtкр, отображенныенасхемаха, б, виг
(рис. 2).
Вслучаяха, б, врасхождениесреднихследуетпризнатьзакономернымпоІ, ІІ, ІІІпорогунадежностисоответственно. Вслучаеграсхождениесреднихнеобходимосчитатьнесущественным.
tкр0,95 |
tкр0,99 |
tкр0,999 |
tкр0,95 |
tкр0,99 |
tкр0,999 |
|
|
t |
|
|
t |
|
tнабл |
|
|
|
tнабл |
|
а |
|
|
б |
|
tкр0,95 |
tкр0,99 |
tкр0,999 |
tкр0,95 |
tкр0,99 |
tкр0,999 |
|
|
t |
|
|
t |
|
|
tнабл |
tнабл |
|
|
|
в |
|
|
г |
|
Рис. 2. Схемысоотношенияtнабл иtкр
12

НаблюдаемоезначениекритерияСтьюдентаtнабл присравнениидвух группдлятрехописанныхслучаевопределяетсяпоформулам:
|
tнабл = |
|
|
|
x − y |
|
|
; |
|
(2.1) |
|||
|
|
|
|
||||||||||
|
|
S 2 |
|
|
S y2 |
|
|||||||
|
|
|
|
|
x |
+ |
|
|
|
|
|
|
|
|
|
|
nx |
ny |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
tнабл = |
x − y |
|
|
|
|
|
|
nxny (nx + ny − 2) |
; |
(2.2) |
|||
Sx2 (nx − 1) + S y2 (ny − 1) |
|
|
|
|
nx + ny |
||||||||
|
|
|
|
|
|
|
|
||||||
|
tнабл = z n(n − 1) . |
|
(2.3) |
||||||||||
|
|
n |
|
− z )2 |
|
|
|||||||
|
|
∑(zi |
|
|
|||||||||
i=1
Вформулах(2.1), (2.2) x , y – средниевгруппах; Sx2 , Sy2 – диспер-
|
1 |
n |
|
сиигрупп; nx , ny – объемыгрупп; вформуле(2.3) zi = xi − yi; z = |
∑ zi, |
||
|
|||
|
n i =1 |
||
п – объем группы.
Лабораторнаяработа№2
Задание1. Определитьразличиевскоростно-силовойподготовке спортсменов-спринтеров по их результатам в тройном прыжке. (Две большиегруппыспопарнонезависимымизначениями. Исходныеданные– приложение2, табл. 1).
Задание2. Определитьлучшуюгруппуспортсменовпопоказателю частоты сердечных сокращений (ЧСС) в состоянии покоя (Две малыегруппыспопарнонезависимымизначениями. Исходныеданные– приложение2, табл. 2).
Задание 3. Определить значимость различий в показателях количества подтягиваний на перекладине в группе спортсменов до начала и в конце периода тренировок силового характера (Две малые группы
13

с попарнозависимымизначениями. Исходныеданные– приложение2, табл. 3).
Пример выполнения лабораторной работы № 2
Задание 1
Результатывтройномпрыжке:
|
nx |
Sx |
y |
ny |
S y |
x |
870 см 46 21,5 см 915 см 39 27,2 см
Подсчитаем наблюдаемое значение критерия Стьюдента tнабл по формуле
tнабл = |
|
|
x − y |
|
|
= |
870 |
− 915 |
= 8,35 . |
|||||
|
|
|||||||||||||
Sx2 |
+ |
Sy2 |
21,52 |
+ |
27,22 |
|||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
46 |
39 |
|
|||
|
nx |
ny |
|
|
|
|||||||||
Числостепенейсвободы k = nx + ny |
− 2 = 46 + 39 − 2 = 83 . |
|||||||||||||
По таблице значений tγ |
|
(приложение 4) найдем tγ = t(γ; k )= |
||||||||||||
= t(0,999; 80)= 3,418. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку tнабл = 8,35 > tγ |
= 3,418, делаем вывод о том, что разли- |
|||||||||||||
чиевскоростно-силовойподготовкедвухгруппспортсменовсуществен- но. Втораягруппаспортсменов, где y = 915 см, наданныймоментготова лучше, чем первая, где x = 815 см.
Задание 2
РезультатыизмеренияЧСС(уд./мин):
xi |
70 |
72 |
73 |
68 |
69 |
nx |
= 5 |
yi |
81 |
69 |
75 |
80 |
82 |
ny |
= 5 |
ВычислениенаблюдаемогозначениякритерияСтьюдентаtнабл проведемпоформуле
tнабл = |
x − y |
|
nxny (nx + ny − 2) |
. |
|
Sx2 (nx − 1) + Sy2 (ny − 1) |
nx + ny |
||||
|
|
|
14
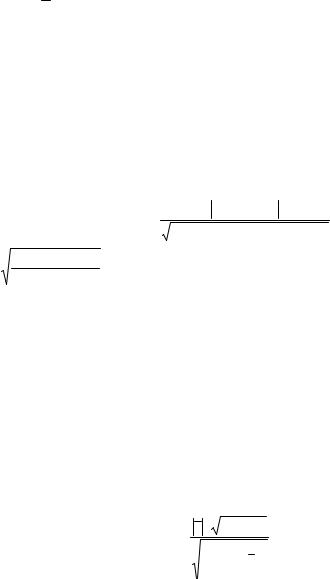
x = 15 (70 + 72 + 73 + 68 + 69)= 70,4;
Sx2 = 15 ((70 − 70,4)2 + (72 − 70,4)2 + (73 − 70,4)2 + (68 − 70,4)2 +(69 −
− 70,4)2 )= 3,44;
|
y = |
1 |
(91+ 69 + 75 + 80 + 82)= 77,4 ; |
|
||||
|
|
|
|
|||||
|
5 |
|
((81− 77,4)2 + (69 − 77,4)2 |
|
|
|
||
|
S y2 = |
1 |
+ (75 − 77,4)2 |
+ (80 − 77,4)2 + (82 − |
||||
|
|
|||||||
|
5 |
|
|
|
|
|||
− 77,4)2 )= 23,44. |
|
|
|
|||||
|
Такимобразом, tнабл = |
70,4 − 77,4 |
× |
|||||
|
|
|
||||||
|
|
|
|
|
3,44 (5 |
− 1) + 23,44 (5 − 1) |
||
× |
5 5 (5 + 5 − 2) = 3,02. |
|
|
|
||||
|
5 + 5 |
|
|
|
||||
|
Числостепенейсвободы k = nx |
+ ny − 2 = 5 + 5 − 2 = 8. |
||||||
|
По таблице значений tγ (приложение 4) |
найдем tγ = t(γ; k )= |
||||||
= t(0,95; 8)= 2,37. Таккак tнабл = 3,02 > tγ = 2,37 , делаемвывод, чторазличиевсредних x = 70,4 < y = 77,4 являетсясущественнымпопервомупорогунадежности(γ = 0,95).
Задание 3
Результатыподтягиваниянаперекладине:
|
xi |
10 |
11 |
12 |
11 |
15 |
|
n = 5 |
|
||
|
yi |
12 |
14 |
10 |
12 |
13 |
|
n = 5 |
|
||
НаблюдаемоезначениекритерияСтьюдентаtнаблвычислимпоформуле |
|||||||||||
|
|
|
|
|
tнабл = z n (n − 1) |
, |
|
||||
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
∑(zi − z)2 |
|
|
||
|
|
|
|
|
|
|
i =1 |
|
|
||
|
|
|
1 |
n |
|
|
|||||
где zi = xi − yi, z = |
|
∑ zi . |
|
|
|||||||
|
|
|
|
||||||||
|
|
|
n i =1 |
|
|
||||||
15
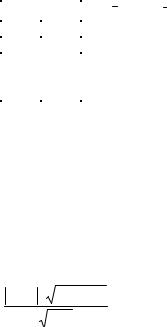
Составимтаблицу.
№ |
xi |
yi |
zi |
zi − |
z |
( zi − |
z |
)2 |
1 |
10 |
11 |
–1 |
–0,8 |
0,64 |
|||
2 |
11 |
14 |
–3 |
–2,8 |
7,84 |
|||
3 |
12 |
10 |
2 |
2,2 |
4,84 |
|||
4 |
11 |
12 |
–1 |
–0,8 |
0,64 |
|||
5 |
15 |
13 |
2 |
2,2 |
4,84 |
|||
Σ |
59 |
60 |
–1 |
|
|
18,8 |
||
Находимгрупповыесредние:
|
5 |
|
1 |
|
|
|
|
|
1 |
5 |
1 |
|
|
|
x = |
1 |
∑xi = |
59 = 11,8; |
y = |
∑ yi = |
60 |
= 12,0; |
|||||||
|
5 |
|
5 |
|||||||||||
|
5 i=1 |
|
|
|
|
|
5 i=1 |
|
|
|||||
|
|
|
|
|
|
5 |
1 |
|
|
|
|
|
|
|
|
|
|
z |
= |
1 |
∑zi = |
(−1) |
= −0,2 . |
|
|
|
|||
|
|
|
|
5 |
|
|
|
|||||||
|
|
|
|
|
|
5 i=1 |
|
|
|
|
|
|
||
Врезультатеполучим: |
|
|
|
|
|
|
|
|||||||
|
|
tнабл |
= |
− 0,2 |
5 (5 − 1) = 0,21. |
|
||||||||
|
|
|
|
|
|
18,8 |
|
|
|
|
|
|||
Определим число степеней свободы по формуле k = 2(n − 1)= = 2(5 − 1)= 8.
По таблице значений tнабл (приложение 4) найдем tγ = t(γ; k )=
= t(0,95; 8)= 2,37.
Заметим, что tнабл = 0,21 < tγ = 2,37 .
Это означает, что существенных различий в среднем количестве подтягиванийдотренировочногоцикла(x = 11,8) ипосленего( y = 12,0)
не обнаружено. Это может свидетельствовать, например, о неэффективноститренировочногопроцесса.
3.ТЕОРИЯКОРРЕЛЯЦИИ
Вспорте, в спортивной команде и в организме спортсмена существуетмноговзаимосвязеймеждуразличнымипризнаками. Например,
сувеличением количества занимающихся в каком-либо виде спорта
16
повышаются результаты; осложнения во взаимоотношениях между игрокамиоднойкомандыухудшаетеерезультативность; сповышением интенсивностинагрузкиуспортсменаповышаетсяпульс, увеличиваетсяскоростькровотокавработающихмышцах, уменьшаютсявнихэнергетические ресурсы и т. д.
СуществуютдвавидасвязимеждупеременнымиX иY: функциональная Y = f (X ), прикоторойкаждомузначениюX соот-
ветствуетединственноезначениеY;
статистическая, при которой на формирование переменных Y и X оказываютвлияниеразличныефакторы. Приэтомсредифакторовесть такие, которые одновременно влияют на переменную X и на переменную Y. В этом случае одному значению переменной X могут соответствоватьнесколькозначенийпеременнойY.
Частным случаем статистической зависимости является корреляционнаязависимость. ВэтомслучаекаждомузначениюX соответствует единственное значение среднего переменной Y: yx = f (x) или
xy = ϕ(y). Последниеуравненияназываютсяуравнениямирегрессии.
Теория корреляции ставит перед собой две задачи. Первая – установитьформукорреляционнойзависимости, тоестьопределитьконк-
ретныйвидфункций f (x) и ϕ(y). Вторая– определитьсилуилитесноту
корреляционнойсвязи.
Решениепервойзадачиначинаетсяспостроениякорреляционного поля– графика, накоторомввидеточекпоказаныпарызначенийY иX, полученныеврезультатеэксперимента.
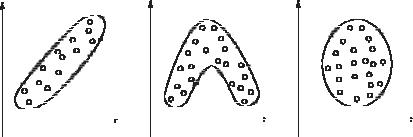
Корреляционноеполеможетвыглядетьтак, какпоказанонарис. 3.1.
y |
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|||
|
|
|
|
|
|
|
|
||||||||||||||
0 |
|
а |
0 |
|
б |
|
0 |
|
|
в |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
Рис. 3.1. Различныевидыкорреляционныхполей:
а, б – связь между переменными х и у скорее всего есть; в – связь отсутствует
17

Еслиустановлено, чтомеждупеременными Y иX имеетместолинейнаязависимость, тоуравнениерегрессииможнозаписатьввиде
|
∑(xi − x)(yi − y) |
|
|||
y = y + |
i |
(x − x); |
(3.1) |
||
∑(xi − x)2 |
|||||
|
i |
|
|
||
x = x + |
∑(xi − x)(yi − y) |
(y − y). |
(3.2) |
||
i |
|||||
|
|
|
|||
|
∑(yi − y)2 |
|
|
|
|
i
В формулах (3.1), (3.2) xi, yi – пары экспериментальных значений переменныхY иX; x , y – средниезначенияX иY соответственно.
Прямые, построенные по уравнениям (3.1) и (3.2), пересекаются в точке A(x, y).
ВопрососилеилитеснотелинейнойкорреляционнойсвязирешаетсяспомощьюкоэффициентакорреляцииПирсонаrxy иранговогокоэффициента Спирмена rs. Первому из них отдается предпочтение в случае, еслиизвестно, чтовыборочныеэкспериментальныеданныеподчиненынормальномузаконураспределения. Обакоэффициентаизменя-
ютсявпределахот (− 1) до (+ 1). Чемближекоэффициентыпомодулю
кединице, темболеесильнойявляетсялинейнаязависимость. Принято считать, чтоеслиуказанныекоэффициенты помодулюменьше0,3, то линейная связь между переменнымиX и Y весьма слаба. Однако заметим, близостькоэффициентовкнулюуказываетлишьнаотсутствиелинейнойсвязи. Можетслучиться, чтосвязьсуществует, ноносит, например, нелинейныйхарактер.
Величиныкоэффициентовкорреляциивычисляютсяпоформулам
∑(xi − x )(yi − y)
rxy = |
i |
, |
(3.1) |
|
∑(xi − x )2 |
||||
|
∑(yi − y)2 |
|
||
|
i |
i |
|
18

6∑(dxi − dyi )2
rs = 1− |
i |
|
, |
(3.2) |
n n2 |
|
|||
|
− 1 |
|
||
где dxi, dyi – ранги переменных X и Y; n – объем выборки.
Приведемпримервычисленияранговогокоэффициентакорреляции rs. Основныевычисления сведены втабл. 3.1.
Таблица 3.1
xi |
№x |
dxi |
yi |
№y |
dyi |
dxi −dyi |
(dxi −dyi )2 |
702 |
1 |
1 |
9,1 |
1 |
1 |
0 |
0 |
730 |
2 |
2 |
9,6 |
2 |
2 |
0 |
0 |
790 |
3 |
3 |
9,8 |
3 |
3 |
0 |
0 |
795 |
4 |
4 |
10,1 |
4 |
4 |
0 |
0 |
802 |
5 |
5 |
10,5 |
6 |
6,5 |
–1,5 |
2,25 |
820 |
6 |
6 |
10,5 |
7 |
6,5 |
–0,5 |
0,25 |
821 |
7 |
7 |
10,3 |
5 |
5 |
2 |
4,0 |
890 |
8 |
8 |
10,7 |
8 |
8 |
0 |
0 |
– |
Σ |
– |
– |
– |
– |
0 |
6,5 |
Замечание. В табл. 3.1 в столбце №у все значения yi пронумерованы в порядке возрастания. НаоснованииэтойнумерациииопределялисьрангипеременнойY.
Вычислимrs:
= − 6 6,5 =
r 1 0,92.
s |
8(82 − 1) |
|
Так как rs = 0,92 близок к единице, заключаем, что переменные X
и Y имеютсильнуюлинейнуювзаимосвязь.
Какправило, достоверностьнайденныхкоэффициентовкорреляции (существенностьихотличияотнуля) проверяютспривлечениемспециальныхтаблиц(приложение5).
Схемапроверкиследующая. Найденныекоэффициентысравниваются с критическими значениями из таблиц для трех уровней доверительнойвероятностиγ = 0,95; 0,99; 0,999. Еслинайденныйкоэффициент оказываетсябольшенаименьшеготабличного, токоэффициенткорреляциидостоверен; есликоэффициентоказываетсяменьшенаименьшего
19

табличного, тодостоверностьнайденногокоэффициентаподвергается сомнению.
Лабораторнаяработа№3
Задание1. Порезультатамтестированиягруппыспортсменовопределить, анализируякорреляционноеполе, существуетливзаимосвязь между показателем индекса Кетле (индекс массы тела) X и становой силыY.
Задание 2. Определить наличие взаимосвязи между показателем индекса Кетле X и становой силы Y у группы спортсменов с помощью расчетаранговогокоэффициентакорреляцииСпирменаикоэффициента корреляцииПирсона.
Задание 3. Найти уравнение регрессии для показателей индекса КетлеX истановойсилыY угруппыспортсменов. Провестиоценкукачества уравнения регрессии, вычисляя остаточные средние квадратическиеотклонения. Показатьпрямыерегрессиинарисунке.
Пример выполнения лабораторной работы № 3
Результатытестированияспортсменов(Сп).
X – индекс Кетле (кг/м2); Y – становая сила (кг).
Сп |
A |
B |
C |
D |
E |
F |
G |
H |
X |
19 |
21 |
23 |
24 |
25 |
29 |
30 |
32 |
Y |
94 |
92 |
96 |
100 |
100 |
98 |
102 |
120 |
Задание 1
Строимкорреляционноеполеиграфикэмпирическойрегрессии, как показанонарис. 3.2.
Анализируякорреляционноеполеиграфикэмпирическойрегрессии, можно сделать вывод о том, что с увеличением индекса Кетле растет истановаясила. Предполагаем, чтоэтидвевеличинысвязываетлинейнаязависимость.
Задание 2
ВычисляемранговыйкоэффициенткорреляцииСпирменапоформуле
|
n |
− dyi )2 |
|
|
6∑(dxi |
||
rs = 1− |
i =1 |
|
, |
n (n2 |
|
||
|
− 1) |
||
20

гдеdxi, dyi – рангипоперемен- |
120 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ным X и Y; n – число пар зна- |
|
|
|
|
|
|
|
|
|
|
|
|
x = 0,42y – 17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
чений(объемвыборки). |
|
|
|
|
|
|
|
|
|
|
|
|
|
y = 1,48x + 63 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Составимтаблицуопреде- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ленияранговдляпеременных |
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
X и Y (табл. 3.2.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подсчитаем rs: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
rs = 1− |
|
6 6,5 |
|
= 0,92 . |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
8(82 − 1) |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Так как |
rs = 0,92 весьма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
близоккединице, томеждупе- |
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ременными X и Y существует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
теснаяположительная линей- |
0 |
|
20 |
25 |
|
|
30 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
ная корреляционная зависи- |
|
|
Рис. 3.2. Корреляционноеполе: |
|||||||||||||||||||||||||||||||||||||||||||||
мость. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Достоверностькоэффици- |
|
1 – графикэмпирическойрегрессии; |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 и 3 – прямые линии регрессии |
|||||||||||||||||||||||||||||||||||||||||||||
ентакорреляцииСпирмена(су- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
щественность его отличия от нуля) проверим, сравнивая его с табличнымизначениямикритическихзначенийrs (приложение5). Втаблице
найдемкритическоезначение rsкр(γ; n)= rsкр(0,99; 8)= 0,881.
Таблица 3.2
xi |
№xi |
dxi |
yi |
№yi |
dyi |
dxi −dyi |
(dxi −dyi )2 |
19 |
1 |
1 |
94 |
2 |
2 |
–1 |
1 |
21 |
2 |
2 |
92 |
1 |
1 |
1 |
1 |
23 |
3 |
3 |
96 |
3 |
3 |
0 |
0 |
24 |
4 |
4 |
100 |
5 |
5,5 |
–1,5 |
2,25 |
25 |
5 |
5 |
100 |
6 |
5,5 |
–0,5 |
0,25 |
29 |
6 |
6 |
98 |
4 |
4 |
2 |
4,0 |
30 |
7 |
7 |
102 |
7 |
7 |
0 |
0 |
32 |
8 |
8 |
120 |
8 |
8 |
0 |
0 |
Σ |
– |
– |
– |
– |
– |
0 |
6,5 |
Поскольку rs > rsкр, делаем вывод о том, что с вероятностью 0,99 найденныйкоэффициентранговойкорреляцииотражаетсуществующую взаимосвязьмеждуиндексомКетлеистановойсилой. Подобнуюзакономерностьможнораспространитьинагенеральнуюсовокупность.
21
