
- •Технические характеристики
- •1.2 Конструкция и принцип действия подъёмника
- •Корректирование нагружаемой силы с учетом динамического воздействия.
- •Расчет определения центра масс и реакций на колесах на примере автомобиля КамАз - 65201
- •Расчет конструкции подъемника.
- •4.1 Расчёт нагрузок при неравномерном заезде автомобиля на подъёмник.
- •1.Средний диаметр винта и гайки:
- •3. Выполняем проверочный расчет винта на продольный изгиб по внутреннему сечению.
- •5. Расчет на прочность кронштейна поперечной балки
- •6. Расчет на прочность сварного шва.
- •7. Определение параметров электродвигателя (мотора-редуктора)
- •7. Эксплуатация, техническое обслуживание и правила техники безопасности.
- •7.1. Требования техники безопасности.
- •7.2. Эксплуатация подъемника.
Расчет конструкции подъемника.
4.1 Расчёт нагрузок при неравномерном заезде автомобиля на подъёмник.
При неравномерном заезде автомобиля на подъёмник (рис.2) нагрузка на опоры не будет распределяться поровну на обе опоры, а будет различной. Логично предположить , что возможно 4 варианта неравномерного заезда автомобиля на подъемник:
переезд и поперечное смещение влево
переезд и поперечное смещение вправо
не доезд и поперечное смещение влево
не доезд и поперечное смещение вправо
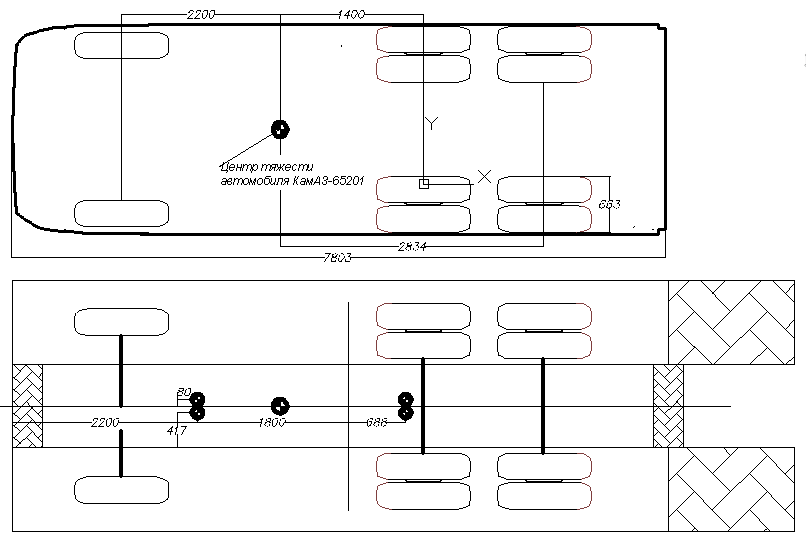
Определим максимально допустимые значения смещения автомобиля при неравномерной установке автомобиля на подъемник.
∆ХMAX – X - смещение по оси ОХ = 1800 мм,
∆ХMAX – У - смещение по оси ОУ = 80 мм.
Для расчета необходимо только два способа неравномерного положения автомобиля - при переезде и недоезде с продольным смещение в одну из сторон, так как расчеты будут аналогичны из-за симметричности платформ подъемника.

Схема сил при неравномерном заезде автомобиля.
 ,
,
 ,
где:
,
где:
 Н
- вес автомобиля с учетам динамических
напряжений;
Н
- вес автомобиля с учетам динамических
напряжений;
 м
- колея автомобиля;
м
- колея автомобиля;
 м
- допустимое смещение автомобиля от
продольной оси подъёмника,
м
- допустимое смещение автомобиля от
продольной оси подъёмника,
Дальнейший расчёт будем проводить с учётом несимметричной постановки автомобиля на подъёмник.
4.2 Расчёт нагрузок на платформу подъёмника.
Определяем реакции в опорах платформы:
Расчётная схема приведена на рисунке

Из
уравнения моментов относительно точки
А находим реакцию
 :
:
Для максимального нагружения:
 .
.
Из
уравнения проекций сил находим реакцию
 :
:
 .
.
4.3 Расчет силовой винтовой передачи
1


2
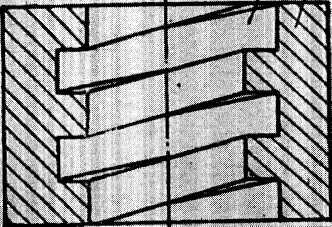
Трапецеидальная
резьба
в профиле – равнобокая трапеция с углом
профиля
(ГОСТ 9484-60); применяется
для силовых винтов, передающих движение
в обе стороны. Пример обозначения
трапецеидальной резьбы: ТРАП40
8.
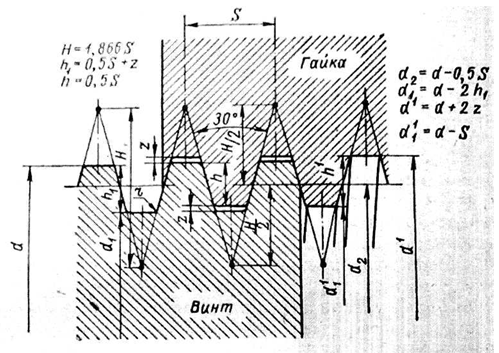
Упорная резьба (ГОСТ 10177-62) предназначена для винтов с большим односторонним усилием (домкраты, тиски).

Рис. 223.
Для грузовых винтов (домкратов, прессов и т. п.) применяется также прямоугольная резьба. Прямоугольная резьба имеет некоторые преимущества перед трапецеидальной (некоторый выигрыш в силе и больший к. п. д.), но она не стандартизована и применяется сравнительно редко по следующим причинам:
-нарезание прямоугольной резьбы сложнее, чем резьбы трапецеидальной (первая может быть нарезана только на токарном станке, а вторая - также и на резьбо-фрезерном - более производительном);
-прямоугольная резьба менее прочна, чем трапецеидальная;
-возникающие при износе зазоры не регулируются, в то время как осевые зазоры в трапецеидальной резьбе можно регулировать стягиванием половинок разрезной гайки.
1.Средний диаметр винта и гайки:

где : Q – вес, приходящийся на каждую стойку (максимальная нагрузка при несимметричной установке автомобиля)
k1 - отношение веса гайки h к среднему диаметру резьбы, принимаем
k1= h/d2 = 1,6
k2 – коэффициент, зависящий от вида резьбы, для трапецеидальной резьбы k2 = 0,5
[q] – допускаемое давление для резьбы, [q] = 10 МПа.
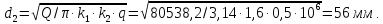 ,
,
С учетом запаса прочности, необходимого для ходового винта подъемника, принимаем трапецеидальную однозаходную правую резьбу с диаметром d2 = 56 мм и шагом h = 3 мм.
Принимаем материал винтовой коры:
для винта – Сталь 45;
для гайки – Бр ОЦС-6-6-3.
Проверяем условие самоторможения винта:
L< ρ,
где L – угол подъема винтовой линии,
ρ – угол трения, для винтовой пары сталь-бронза ρ = 4º.
L = arctg (p/(π * dcp ),
где р – шаг резьбы, р = 3 мм.
L = arctg (3/(3,14 * 56)) = 0,98 º,
так как 0,98 º< 4º, то условие самоторможения выполняется.
Коэффициент полезного действия винтовой пары
η = tg L/tg (L + ρ),
η = tg 0,98/tg (0,98 + 4) = 0,19
2. Выполним проверку винта на прочность с учетом совместного действия деформации сжатия и кручения.
Условие прочности:
σпр < [σ],
где σпр – приведенное напряжение от действия деформации сжатия и кручения
[σ] – допускаемое напряжение.
σпр = √(σсж2+4τ2),
где σсж – напряжение сжатия,
τ – касательное напряжение.
σсж = 4Q/(π * d22) ,
Q
= dcp2*π*k1*k2*[q]
= 0,0562*3,14*1,6*0,5*10*106
=
 Н
Н
σсж
= 4 * /3,14*0,0562
=
32,7*106
Па = 32,7 МПа,
/3,14*0,0562
=
32,7*106
Па = 32,7 МПа,
τ = Мкр/Wр ,
где Мкр – крутящий момент, прилагаемый к винту,
Wр – полярный момент сопротивления
Мкр = 0,5*Q*d22*tg(L+ρ)+Мп ,
где Мп – момент трения на опорах винта
Мп = 0,25*d2*Q*f0 ,
где f0 – коэффициент трения в подшипниках, f0=0,01
Мп
= 0,25*0,056* *0,01
= 11,3 Н*м
*0,01
= 11,3 Н*м
Мкр
= 0,5* *0,0562*tg(0,98
+ 4) + 11,3 = 22,3 Н*м
,
*0,0562*tg(0,98
+ 4) + 11,3 = 22,3 Н*м
,
Wp = π*dв3/16 ,
dв = d2-H1-ac ,
где Н1 – высота профиля, Н1= 5 мм,
aс – зазор по вершине резьбы, aс = 0,25.
dв = 56 - 5 - 0,25= 50,25 мм
Wр = 3,14*0,050253/16 = 25*10-6мм3
τ = 22,3/25*10-6 = 0,896 МПа
σпр = √(322+4*0,8962) = 32 МПа,
σпр = 32 МПа < [σ] = 160 МПа, - следовательно, условие прочности выполняется.
