10.3. Средние индексы из индивидуальных

Общие индексы могут быть рассчитаны не только как агрегатные, но и как средние из индивидуальных или групповых. Если агрегатный индекс нельзя вычислить, тогда его заменяет средний индекс, тождественный агрегатному.

Общий индекс по своему смыслу является средней величиной из индивидуальных индексов. При этом возникает вопрос, какую форму средней и какие веса в ней следует применить. Форму средней и систему весов выбирают на основании общего правила: агрегатный индекс это основная форма экономического индекса. Отсюда следует, что средний из индивидуальных индексов должен быть тождественен исходному агрегатному или средний индекс является преобразованной формой агрегатного индекса.

В статистической практике средние индексы рассчитываются преимущественно в форме среднего арифметического и среднего гармонического индексов: 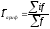и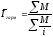

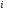- индивидуальные индексы,

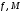- веса соответственно в среднем арифметическом и среднем гармоническом индексе.

1. Индекс физического объема

Индекс физического объема может быть преобразован в средний арифметический индекс. При этом должно соблюдаться тождество:

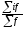
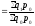
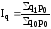; i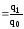,отсюда q₁=i∙q₀.

Заменим q₁ на произведение (i∙q₀) в формуле агрегатного индекса и получим .

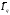
В таком виде агрегатный индекс физического объема услуг есть средняя арифметическая из индивидуальных индексов, взвешенных по стоимости услуг базисного года (q₀p₀).

Аналогично, определяя веса среднегармонического индекса физического объема, необходимо помнить о соблюдении условия:

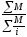
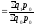
Тогда, выражая продукцию базисного периода как 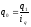, осуществляем замену в знаменателе агрегатного индекса физического объема. В результате получаем общийиндекс физического объема в форме среднего гармонического индекса: =

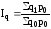Такое преобразование наглядно показывает тождество между агрегатным индексом и средним арифметическим и средним гармоническим индексами физического объема.

При решении конкретных задач выбор той или иной формы среднего индекса определяется прежде всего тем, какие имеются исходные данные.

2. Индекс цен

Средние арифметические и средние гармонические индексы являются модификациями агрегатных индексов, т.е. применительно к индексам цен должны соблюдаться следующие равенства:

А) по Ласпейресу:

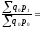
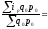
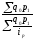
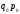- весами служит стоимость отдельных видов продукции базисного периода,

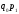- весами служит стоимость отдельных видов продукции базисного периода в отчетных ценах.

б) по Пааше

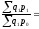
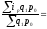
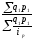
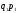- весами служит стоимость отдельных видов продукции отчетного периода.

Т.о. значения среднего арифметического и среднего гармонического индексов цен будут совпадать тогда, когда их веса определены из тождества одной и той же агрегатной формуле (по Ласпейресу или Пааше).

Однако средние индексы по Ласпейресу не тождественны одноименным средним индексам по Пааше, как не тождественны и сами агрегатные индексы цен Ласпейреса и Пааше. Поэтому при расчете общего индекса как среднего из индивидуальных необходимо указывать, модификацией какого агрегатного индекса является используемый средний индекс, т.к. это определяет его веса.