8.8. Теоретическое корреляционное отношение

Показателями тесноты корреляционной связи служат коэффициент и индекс корреляции.

Теснота связи между признаками измеряется с помощью показателей вариации результативного признака y.

Обратимся к рис. 8.1, на котором изображены три линии:

y – ломаная, называемая эмпирической линией регрессии, которая отражает фактические значения y при соответствующих значениях факторного признака х;

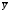–прямая линия, параллельная оси абсцисс, соответствующая среднему значению y при исключении влияния всех факторов;

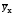–выравненная линия регрессии, характеризующая значения y при абстрагировании всех факторов, кроме фактора х.

Поскольку на y помимо х оказывают влияние и другие факторы, то линия y не совпадает с линией 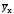. Это несовпадение свидетельствует о неполной связи между y и х.

Чтобы измерить, насколько связь близка к функциональной, исчисляют показатели тесноты связи. Для этого необходимо оценить вариацию результативного признака y, вызванную только влиянием признака х, и остаточную его вариацию, обусловленную прочими факторами.

Общая дисперсия результативного признака

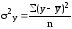
характеризует вариацию y под влиянием всех факторов.

Средний квадрат отклонений 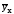от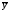

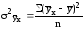
измеряет вариацию y только под влиянием фактора х – это факторная дисперсия. Средний квадрат отклонений y от

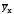
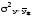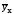= (y–)²/n

характеризует остаточную вариацию y под влиянием всех остальных факторов.

В математической статистике доказано, что

²_y = 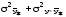, т.е..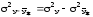

Поэтому эту дисперсию называют остаточной дисперсией, она характеризует вариацию y за счет остальных факторов, не включенных в уравнение регрессии.

Теснота связи между y и х измеряется отношением факторной дисперсии к общей дисперсии результативного признака, называемым теоретическим индексом детерминации, .

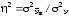Теоретический индекс детерминации характеризует долю вариации результативного признака под влиянием факторного признака в общей колеблемости результативного признака. Если между признаками имеется корреляционная связь, то по мере ее усиления, т.е. повышения тесноты связи между результативным и факторным признаками, индекс детерминации увеличивается, а по мере ослабления – уменьшается. Таким образом, индекс детерминации характеризует тесноту связи, близость корреляционной связи к функциональной.

Корень квадратный из индекса детерминации есть индекс корреляции или теоретическое корреляционное отношение. Индекс корреляции, или теоретическое корреляционное отношение, характеризует тесноту связи при любой форме зависимости. Остаточная дисперсия 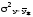необходима для выбора наилучшей функции, которая в наибольшей степени выравнивает (аппроксимирует) эмпирическую линию регрессии.Аппроксимирующую функцию выбирают по минимуму остаточной дисперсии или .

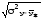Частным случаем индекса корреляции является линейный коэффициент корреляции r, который применяется для оценки тесноты связи при линейной зависимости.

При прямолинейной связи линейный коэффициент корреляции тождествен индексу корреляции, они численно равны: .

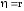Корреляционное отношение – универсальный показатель, применимое ко всем случаям корреляционной зависимости независимо от формы этой связи.

Следует различать эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается по аналитической группировке (или корреляционной таблице) как корень квадратный из отношения межгрупповой дисперсии результативного признака к общей дисперсии результативного признака. Теоретическое корреляционное определяется на основе выровненных (теоретических) значений результативного признака, рассчитанных по уравнению регрессии (для любой формы связи).

Эмпирическое и теоретическое корреляционное отношение определяются по формулам:

,

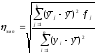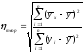
где 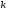- число групп по факторному признаку,- число единиц совокупности,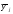- среднее значение признака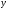в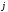-й группе;

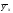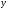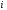- значение для-й единицы совокупности, рассчитанное по уравнению регрессии.