8.6. Показатели тесноты связи между двумя количественными признаками

Связь между количественными признаками измеряется через их вариацию. Измерить зависимость (связь) между двумя коррелируемыми величинами – значит определить, насколько вариация результативного признака обусловлена вариацией факторного признака.

В качестве показателей тесноты связи между количественными признаками, кроме коэффициента Фехнера, наиболее часто используются линейный коэффициент корреляции, коэффициент корреляции рангов, коэффициент конкордации, а также эмпирическое и теоретическое корреляционное отношение.

Линейный коэффициент корреляции

Линейный коэффициент корреляции r применяется для оценки тесноты связи при линейной зависимости.

Как и коэффициент Фехнера, линейный коэффициент вариации может быть построен на основе отклонений индивидуальных значений признаков и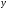от их средних величин. Но в отличие от коэффициента Фехнера в линейном коэффициенте корреляции учитываются не только знаки, но и значения отклонений (х–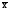) и (y–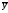). Чтобы обеспечить соизмеримость отклонений признакови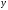по абсолютным размерам и единицам измерения, рассчитывают их нормированные отклонения:t_x = (x–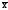)/_x; t_y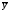 = (y–)/_y ,

где _x, _y – средние квадратические отклонения признаков х и y.

Линейный коэффициент корреляции представляет собой среднюю величину из произведения нормированных отклонений по обоим признакам: .

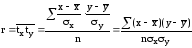Числитель последней формулы, деленный на , представляет собой среднее произведение отклонений значений двух признаков от их средних, называемое ихковариацией:

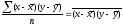
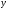Следовательно, можно сказать, что линейный коэффициент корреляции представляет собой частное от деления ковариации между ина произведение их средних квадратических отклонений.

Для упрощения расчетов линейного коэффициента корреляции пользуются преобразованной формулой:

.

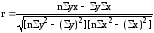Линейный коэффициент вариации можно рассчитать и по формуле: ,

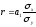где 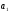- коэффициент регрессии в уравнении связи (см. ниже).

Коэффициент корреляции принимает значения от -1 до +1, показывая не только тесноту, но и направление связи. Знак "+" указывает на прямую зависимость между результативным и факторным признаками, знак «–» – на обратную зависимость между ними. Если r=0, то связь между признаками отсутствует. Чем ближе r к единице, тем теснее связь между рассматриваемыми признаками. Если 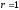, то это означаетфункциональную зависимость между и.

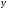8.7. Определение уравнения регрессии между двумя переменными

Применение корреляционно-регрессионного метода анализа явлений начнем с оценки парной корреляции и построения однофакторной модели зависимости результативного признака от факторного в виде уравнения корреляционной связи. Уравнение корреляционной связи часто называют уравнением регрессии, показывающим вид зависимости среднего значения результативного признака от факторного.

Определить уравнение регрессии – значит по эмпирическим данным математически описать изменения взаимно коррелируемых величин.

Уравнение регрессии можно назвать теоретической линией регрессии. Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими.

Аналитическая связь между результативным и факторным признаками может описываться уравнениями:

прямой 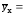a₀ + a₁x ;

гиперболы 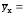a₀ + a₁/x ;

параболы 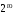порядка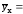a₀ + a₁x +a₂x² ;

степенной функции 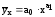и т.д.

Прежде чем приступить к построению модели – уравнения регрессии, необходимо выбрать тип функции, т.е. форму корреляционной связи. Определить в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками – одна из основных задач регрессионного анализа.

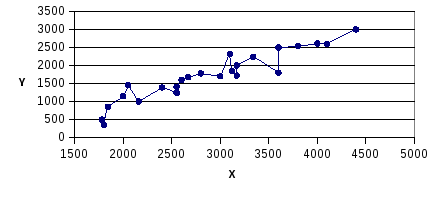
Некоторые данные о форме связи можно получить из графика эмпирической линии регрессии. Если на корреляционном поле соединить точки отрезками прямой, то получится ломаная линия с некоторой тенденцией к росту или снижению, которая и называется эмпирической линией регрессии. На рис. 8.1 представлена в качестве примера эмпирическая линия регрессии заработной платы работников предприятия от их производительности труда.

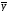
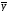
y

y

Рис. 8.1. График корреляционной зависимости заработной платы (y)

и производительности труда (x)

Изломы эмпирической линии регрессии y обусловлены тем, что на результативный показатель оказывают влияние кроме х другие факторы. Если отвлечься (абстрагироваться) от влияния других факторов, кроме х, то можно сделать вывод о виде аналитической функции y_x, в определенной степени отражающей характер зависимости между y и х. В данном случае можно склониться к прямолинейной форме связи.

После выбора вида зависимости приступают к расчету параметров аналитического уравнения корреляционной связи (уравнения регрессии).

Параметры находят на основе метода наименьших квадратов.

Метод наименьших квадратов заключается в минимизации квадратов отклонений фактических данных y от теоретических 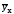(выравненных по уравнению регрессии):.

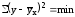Для нахождения параметров уравнения прямой 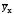= а₀+а₁х используется система нормальных уравнений вида

a₀n+a₁x=y,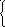

a₀x+a₁x²=xy,

где n – объем исследуемой совокупности (число единиц наблюдения).

Решение этой системы относительно а₀ и а₁ позволяет определить параметры уравнения регрессии:

; .

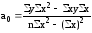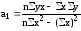Параметр 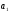в уравнении линейной регрессии называетсякоэффициентом регрессии.

Коэффициент регрессии показывает, на сколько (в абсолютном выражении) изменяется значение результативного признака при изменении факторного признака на единицу.

По уравнению регрессии можно найти выровненные теоретические значения результативного признака при соответствующих значениях фактора х. Отклонения фактических значений y от теоретических 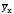обусловлены тем, что регрессия y строилась только по одному фактору х, в то время как в действительности y зависит от множества факторов.