8.3. Изучение связи между двумя атрибутивными (качественными, описательными) признаками

Для определения тесноты связи двух качественных признаков (c альтернативной вариацией признака), каждый из которых состоит из двух групп, рассчитывают коэффициенты ассоциации 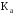и контингенции 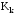на основе построения таблицы сопряженности:

a	b	a + b
c	d	c + d
a + c	b + d	a + b + c + d

Таблица сопряженности размерностью 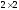называется «таблицей 4-х полей», частоты признака в полях таблицы обозначим соответственно.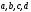

Таблица показывает связь между двумя явлениями с альтернативной вариацией признака.

Коэффициенты ассоциации служит для определения тесноты связи двух признаков с альтернативной вариацией, и рассчитывается по формуле:.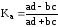

Недостаток коэффициента ассоциации: если в одной из 4-х клеток таблицы частота равна нулю, значение коэффициента ассоциации по модулю будет равно единице, что преувеличивает меру действительной связи.

Коэффициент контингенции 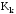служит для определения тесноты связи двух качественных признаков, каждый из которых состоит из двух групп, и рассчитывается по формуле:.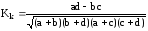

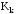Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается существенной, если ≥0,5;≥0,3.

8.4. Измерение связи по таблицам взаимной сопряженности

Если каждый из качественных признаков состоит из большого числа групп (более двух), то теснота связи измеряется на основе таблицы сопряженности с помощью коэффициентов взаимной сопряженности Пирсона и Чупрова.

Таблица сопряженности в этом случае имеет вид:

Y X	I	II	III	Всего
I			nxy	nx
II				nx
III				nx
Итого	ny	ny	ny	n

Коэффициент взаимной сопряженности Пирсона ;

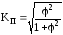где 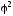– показатель взаимной сопряженности:;

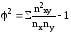n_xy – частота каждой клетки таблицы взаимной сопряженности, (т.е. частоты взаимного сочетания 2-х атрибутивных (описательных) признаков);

n_x, n_y – итоговые частоты соответствующих строк и столбцов.

Недостаток коэффициента Пирсона в том, что он не достигает единицы и при полной связи признаков, а лишь стремится к единице при увеличении числа групп.

Более совершенная мера связи предложена Чупровым.

Коэффициент взаимной сопряженности Чупрова ,

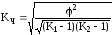К₁, К₂ – число строк и столбцов.

Коэффициент взаимной сопряженности Чупрова может достигать предельного значения, равного единице, только в случае квадратной таблицы (m=p): чем более несимметрична таблица, тем больше коэффициент Чупрова отличается от единицы при полной связи признаков. Как привило, коэффициент Чупрова гораздо строже оценивает тесноту связи, чем коэффициент Пирсона, слишком быстро приближающийся к единице.

8.5. Измерение тесноты связи между порядковыми переменными

Коэффициент корреляции рангов  (коэффициент Спирмена) учитывает согласованность рангов. (Ранг – порядковый номер, присваиваемый каждому значению факторного и результативного признака в ранжированном ряду).

Коэффициент Спирмена рассчитывается по формуле: ,

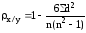где n – количество единиц совокупности; d – разность рангов по признакам х и y.

Порядок сопоставления рангов факторного и результативного показателей таков: единицы совокупности ранжируются по факторному и результативному признакам и каждой единице присваивается номер (место) в упорядоченном ряду признаков. Если встречаются в ряду одинаковые варианты по результативному и факторному признакам, то каждой из них присваивается среднее арифметическое значение их рангов, т.е. наблюдаются т.н. связанные ранги.

Коэффициент корреляции рангов может принимать значения от –1 до +1. Значение = +1 означает строгое изменение рангов в одном направлении, = –1 – в противоположном, при = 0 связь отсутствует.

Недостаток коэффициента корреляции рангов: одинаковым разностям рангов могут соответствовать неодинаковые разности значений признаков (количественных). Следовательно, для количественных признаков 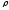является приближенной мерой тесноты связи.

Коэффициент конкордации (множественный коэффициент ранговой корреляции) применяют для определения тесноты связи между произвольным числом признаков:

,

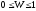
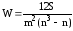где m – количество факторов, n – число единиц наблюдения (ранжируемых единиц),

S – отклонение суммы квадратов суммы рангов по всем факторам от среднего квадрата суммы рангов.