6.5. Малая выборка

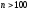В процессе оценки степени представительности данных выборочного наблюдения важное значение приобретает вопрос об объеме выборочной совокупности . При большом числе единиц выборочной совокупности () распределение случайных ошибок выборочной средней нормально или приближается к нормальному по мере увеличения числа наблюдений. Вероятность выхода ошибки за определенные пределы оценивается на основе таблиц интеграла Лапласа.

Но уже при 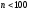возникает несоответствие между табличными значениями и вероятностью предела; при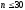погрешность становится значительной. Несоответствие обусловлено характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, т.к. распределение ошибок выборки при большой выборке всегда оказывается нормальным.

В выборках небольшого объема 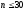характер распределения генеральной совокупности сказывается на распределении ошибок выборки. Поэтому для расчета ошибки выборки при небольшом объеме наблюдения (уже менее 100 единиц) отбор должен проводиться из совокупности, имеющей нормальное распределение.

Малой называют выборку, объем которой находится в пределах 5...30 ед.

Особенностью малой выборки является то, что ее случайные ошибки не подчиняются закону нормального распределения, а имеют особый закон распределения. Поэтому при оценке результатов малой выборки нельзя пользоваться формулами собственно случайного отбора.

Результаты малой выборки оцениваются по закону распределения вероятностей Стьюдента.

Английский математик Стьюдент доказал, что вероятность того, что |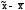|<t*,

является функцией от t* и n, где n – численность выборки, t* – отношение Стьюдента.

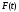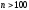В 1908 г. им было построено специальное распределение, которое позволяет и при малых выборках соотносить и доверительную вероятность. Притаблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при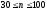различия незначительны. Поэтому приактически к малым выборкам относят выборки объемом менее 30 единиц.

Плотность вероятностей распределения Стьюдента описывается функцией ,

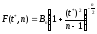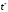- текущая переменная (критерий Стьюдента),

- объем выборки,

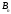- величина, зависящая лишь от .

При оценке результатов малой выборки величина генеральной дисперсии в расчетах не используется. Для определения возможных пределов ошибки пользуются так называемым критерием Стьюдента, определяемым по формул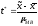е , где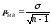- мера случайных колебаний выборочной средней в малой выборке.

Величина вычисляется на основе данных выборочного наблюдения: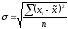

Данная величина используется лишь для исследуемой совокупности, а не в качестве приближенной оценки в генеральной совокупности.

Распределение Стьюдента имеет параметр «число степеней свободы» -

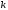
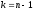
При небольшой численности выборки распределение Стьюдента отличается от нормального: большие величины критерия имеют здесь большую вероятность, чем при нормальном распределении. При увеличении объема выборки, а следовательно, и числа степеней свободы распределение Стьюдента быстро приближается к нормальному.

На практике пользуются таблицами распределения Стьюдента S(t*), в которых для различных n и t* приведены вероятности Р(t*). В табл. 10.1 даны значения доверительной вероятности Р(t*), рассчитанные для различных t* и k (k – число степеней свободы, равное n–1).

Таблица 10.1. Доверительная вероятность Р(t*)

t*	Степени свободы k
	4	5	6	7	8	9	10	15	20	
2,0 2,5 3,0	0,844 0,933 0,960	0,898 0,946 0,970	0,908 0,953 0,976	0,914 0,959 0,980	0,919 0,963 0,983	0,923 0,966 0,985	0,927 0,969 0,987	0,936 0,976 0,991	0,941 0,979 0,993	0,954 0,988 0,997

По этой таблице определяется двусторонний критерий, т.е. вероятность того, что фактическое значение t* по случайным причинам не будет больше табличного по абсолютной величине.

Средняя ошибка малой выборки рассчитывается по формуле _мв =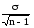или.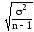

Предельная ошибка малой выборки равна _мв=t*∙ _мв.