
- •1. Предмет и метод статистики
- •1.1 Возникновение и определение статистики
- •1.2. Предмет статистики и особенности статистики как науки
- •1.3. Статистические закономерности
- •1.4. Признаки
- •1.5. Метод статистики
- •1.6. Организация государственной статистики в рф
- •2. Средние величины
- •3. Статистическое наблюдение
- •3.1. Понятие статистического наблюдения. Этапы его проведения
- •3.2. Методологические вопросы статистического наблюдения
- •3.3. Основные организационные формы, виды и способы статистического наблюдения
- •Статистическое наблюдение
- •3.4. Статистическая отчетность
- •3.5. Требования, предъявляемые к данным стат. Наблюдения
- •3 Этап сн: подготовка данных к обработке
- •4. Вариационные ряды и их характеристика
- •4.1. Вариация массовых явлений
- •4.2. Построение вариационного ряда. Виды рядов. Ранжирование данных
- •4.3. Определение числа групп и величины интервала
- •4.4. Плотность распределения
- •4.5. Графическое изображение вариационного ряда
- •4.6. Структурные средние
- •Мода распределения
- •Медиана распределения
- •4.7. Другие структурные характеристики вариационного ряда Квартили и децили распределения
- •4.8. Показатели размера и интенсивности вариации
- •4.9. Свойства дисперсии и способы ее расчета
- •4.10. Дисперсия альтернативного признака
- •4.11. Виды дисперсий и правило их сложения
- •4.12. Закономерности распределения
- •4.13. Закон нормального распределения
- •4.14. Моменты распределения
- •4.15. Асимметрия распределения
- •4.16. Эксцесс распределения
- •5. Статистическая сводка. Группировка данных наблюдений. Таблицы
- •5.1. Статистическая сводка
- •5.2. Группировка данных
- •5.3. Определение числа групп и величины интервалов
- •5.4. Виды группировок
- •Типологические группировки
- •Структурные группировки
- •Аналитические группировки
- •5.5. Классификации
- •5.6. Сопоставимость статистических группировок
- •5.7. Статистические таблицы
- •6. Выборочное наблюдение и его организация
- •6.1. Выборочное наблюдение. Принципы теории выборки
- •6.2. Ошибки репрезентативности. Ошибки выборки
- •6.3. Определение необходимого объема выборки
- •6.4. Виды отбора единиц в выборочную совокупность
- •6.5. Малая выборка
- •6.6. Моментные наблюдения
- •7. Статистические показатели
- •7.1. Сущность статистических показателей
- •Границы объекта:
- •Статистический показатель
- •7.2. Классификация статистических показателей
- •7.3. Абсолютные показатели
- •7.4. Относительные показатели
- •8. Статистические методы изучения взаимосвязи между явлениями
- •8.1. Понятие корреляционной зависимости
- •8.2. Методы выявления корреляционной связи
- •Метод группировок
- •8.3. Изучение связи между двумя атрибутивными (качественными, описательными) признаками
- •8.4. Измерение связи по таблицам взаимной сопряженности
- •8.5. Измерение тесноты связи между порядковыми переменными
- •8.6. Показатели тесноты связи между двумя количественными признаками
- •Линейный коэффициент корреляции
- •8.7. Определение уравнения регрессии между двумя переменными
- •8.8. Теоретическое корреляционное отношение
- •8.9. Множественная корреляция
- •9. Ряды динамики
- •9.1. Понятие о рядах динамики. Их виды
- •9.2. Сопоставимость уровней ряда.
- •9.3. Основные показатели рядов динамики
- •Методы выявления основной тенденции в рядах динамики
- •Выявление и измерение сезонных колебаний
- •Измерение колеблемости в рядах динамики
- •Автокорреляция в рядах динамики
- •Определение уравнения авторегрессии
- •Элементы прогнозирования
- •10. Виды и способы построения индексов
- •10.1. Понятие об индексах. Их виды
- •10.2. Агрегатные индексы
- •1. Агрегатный индекс физического объема.
- •2. Агрегатный индекс цен
- •10.3. Средние индексы из индивидуальных
- •1. Индекс физического объема
- •2. Индекс цен
- •10.4. Индексы переменного и постоянного составов. Индекс структурных сдвигов
- •Iпост .
- •10.5. Цепные и базисные индексы
- •10.6. Определение роли отдельных факторов в динамике результативных показателей
- •10.7. Территориальные индексы
5.3. Определение числа групп и величины интервалов
Вместе с выбором группировочного признака возникает задача определения количества групп, на которые следует подразделить изучаемое явление.
Число групп зависит от:
задач исследования
вида признака, положенного в основу группировки
численности совокупности
степени вариации признака
Единицы анализируемой совокупности могут быть разбиты по одному и тому же признаку на разное число групп. Например, при группировке населения по возрасту с целью определения трудовых ресурсов страны все население делится на три группы: население моложе трудоспособного возраста, трудоспособное население и население старше трудоспособного возраста. Если же анализируется продолжительность жизни, то строится более детальная группировка и выделяются группы по 5 лет.
При группировке по атрибутивному (описательному) признаку вопрос о количестве групп решается сравнительно просто – по количеству градаций, видов состояния этого признака.
Например, группировка населения по полу образует две группы, организаций связи по федеральным округам – 7 групп, по формам собственности – на пять групп: государственная, муниципальная, частная, смешанная, собственность иностранных юридических лиц.
Если атрибутивный (описательный) признак имеет множество наименований (например, профессия – в отрасли связи насчитывается несколько десятков их наименований), то для статистической характеристики состава работников образуют укрупненные группы (руководители, специалисты, рабочие, прочие). Такое объединение основано на изучении сущности производственных процессов.
Характеристика типов предприятий по их величине часто ограничивается тремя группами: мелкие, средние и крупные, а при изучении рентабельности – группы нерентабельных, рентабельных и высокорентабельных.
Группировки по количественному признаку очень разнообразны. При выборе числа групп в совокупности с количественным признаком необходимо, чтобы в каждую группу попало достаточное количество единиц совокупности. Только в этом случае обобщающие характеристики каждой группы (средние, относительные показатели) будут устойчивыми, неслучайными, характерными.
Сравнительно просто образуются группы по количественным признакам, имеющим дискретную (прерывную) вариацию и принимающим целые значения.
Если количественный признак изменяется в широких пределах и имеет множество различных значений, то каждая группа образуется в виде интервалов.
Группировка может быть выполнена с равными и неравными интервалами.
Равные интервалы употребляются в тех случаях, когда признак изменяется более или менее равномерно в ограниченных пределах, например масса письма, посылки, заработная плата определенной категории работников.
Величина интервала зависит от размаха варьирования признака и численности изучаемой совокупности и в случае равных интервалов может определятся по формуле Стерджесса.
Формула Стерджесса служит для определения величины интервала:
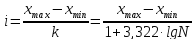
где i – интервал, т.е. разница между максимальным xmax и минимальным xmin значениями признака в каждой группе; N – численность единиц совокупности; k – число групп, которое оптимально при величине 1+3,322 lg N.
Недостаток формулы Стерджесса состоит в том, что её применение дает хорошие результаты для большой совокупности единиц и когда распределение единиц по признаку, положенному в основание группировки, близко к нормальному.
Число групп можно определить также по следующей номограмме:
|
Численность единиц совокупности |
15..24 |
25..44 |
45..89 |
90..179 |
180..359 |
360..719 |
720..1439 |
|
Число групп |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Другим способом выполнения группировки является использование среднего квадратического отклонения . Если величина интервала равна 0,5, то совокупность разбивается на 12 групп, если 2/3 или, то совокупность делится на 9 или 6 групп.
При
 ,
,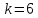 интервалы групп выглядят следующим
образом:
интервалы групп выглядят следующим
образом:
от
 до
до
от
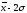 до
до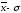
от
 до
до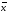
от
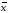 до
до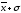
от
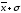 до
до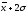
от
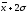 до
до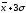
Однако при определении групп данными методами возможно получение пустых или малочисленных групп. Если размах вариации признака совокупности велик и его значения варьируют неравномерно, то используют группировку с неравными интервалами.
Неравные интервалы употребляются в тех случаях, когда признак изменяется неравномерно. Из неравных интервалов чаще всего употребляются прогрессивно возрастающие или убывающие интервалы.
Величина интервалов,
изменяющихся в арифметической прогрессии,
определяется по формуле:
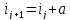 ,
,
в геометрической
прогрессии:
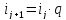
где a – постоянная величина (положительная для прогрессивно-возрастающих интервалов, отрицательная – для прогрессивно-убывающих);
q – константа – положительное число (для прогрессивно-возрастающих интервалов q > 1, для прогрессивно-убывающих – q < 1).
Например, необходимо построить группировку предприятий отрасли по показателю выручки от реализации продукции, который варьирует от 500 млн. руб. до 4000 млн. руб. в год, то строить группировку с равными интервалами нецелесообразно, т.к. как правило, совокупность предприятий любой отрасли промышленности и торговли включает большое число малых предприятий, имеющих небольшую выручку. С ростом выручки от реализации продукции значительно снижается число предприятий. Т.о. распределение числа предприятий по величине выручки является неравномерным. Поэтому следует построить группировку с неравными интервалами.
Таблица
Группировка предприятий с неравными интервалами
|
№ группы |
Интервал |
|
I II III IV V |
500-800 800-1300 1300-2000 2000-2900 2900-4000 |
Величина каждого последующего интервала у этой группировки больше предыдущего на 200 млн. руб., т.е. увеличивается в арифметической прогрессии.
При образовании интервалов важное значение имеет точное обозначение границ.
Например, группы предприятий по численности работников: 200 – 600, 600 – 1000. Такая запись предполагает, что единица, у которой значение признака совпадает с верхней границей интервала, относится к следующей группе.
Обычно границы интервалов обозначаются указанием значений признака «от» и «до» (в нашем примере – 200 – 599, 600 -999). Характер такого обозначения говорит, что в группу включаются все значения признака в указанных границах.
После определения группировочного признака и границ групп строится ряд распределения.
Статистический ряд распределения – это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку. В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по описательным (качественным) признакам. Вариационными называют ряды распределения, построенные по количественному признаку.
