4.16. Эксцесс распределения

Для характеристики степени отклонения симметричного распределения от нормального по ординате используется показатель островершинности, крутизны распределения, называемый эксцессом: Ex = (₄/⁴) – 3,

где ⁴ – центральный момент четвертого порядка.

Для нормального распределения Ех=0, т.е. ₄/⁴=3.

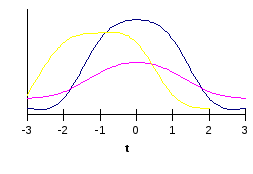
У высоковершинных (по сравнению с нормальным) кривых эксцесс положительный, у низковершинных отрицательный (рис. 4.4).

Рис. 4.4. Характеристика распределений в соответствии с эксцессом: 1 – высоковершинное, 2 – нормальное, 3 – низковершинное.

Часто эксцесс интерпретируется как «крутизна» распределения, но это неточно и неполно. График распределения может выглядеть сколь угодно крутым в зависимости от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Для того чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной ) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными.

Показатели эксцесса и асимметрии необходимы в статистическом анализе для определения неоднородности совокупности, асимметричности распределения и близости эмпирического распределения к нормальному закону. При значительных отклонениях показателей асимметрии и эксцесса от нуля нельзя признать совокупность однородной, а распределение близким к нормальному.

Чтобы оценить существенность эксцесса распределения, рассчитывают среднюю квадратическую ошибку эксцесса:

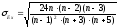
Распределение можно считать нормальным, а точнее говоря, не следует отвергать гипотезу о сходстве фактического распределения с нормальным, если:

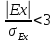
5. Статистическая сводка. Группировка данных наблюдений. Таблицы

5.1. Статистическая сводка

Статистическая сводка является второй стадией статистического исследования.

Статистическая сводка состоит в систематизации первичных данных, образовании статистической совокупности и получении итоговых абсолютных обобщающих показателей, группировке данных по количественным и качественным признакам и представлении их в табличной и графической формах.

На этой стадии переходят от изучения отдельных единиц к изучению их совокупности. Результатом сводки является сводная характеристика всей совокупности (всего объекта).

По глубине обработки данных сводка может быть простой и сложной.

Простая сводка предусматривает суммирование значений признаков и получение итогов по совокупности единиц наблюдения.

Простая сводка применяется в качественно однородной совокупности единиц и чаще всего выступает не самостоятельно, а как один из этапов сложной сводки.

Сложная сводка предполагает сначала распределение отдельных единиц изучаемого объекта по группам, а затем уже статистическую характеристику каждой группы и в целом всего объекта.

В подавляющем большинстве случаев применяется сложная сводка, поэтому статистическая сводка в широком понимании включает комплекс статистических приемов, направленных на группировку и характеристику изучаемого явления обобщающими абсолютными показателями.

Статистическая сводка проводится по определенной программе, разрабатываемой исходя из целей и задач статистического исследования. В программе сводки предусматриваются: выбор группировочных признаков, определение порядка формирования групп, разработка показателей для характеристики групп и явления (объекта) в целом; подсчет групповых и общих итогов; оформление конечных результатов сводки в статистических таблицах.

Как правило, программа сводки задается в виде макетов статистических таблиц и часто бывает известна уже в период проведения статистического наблюдения. Так, в формах статистической отчетности уже заложены важнейшие экономико-статистические группировки.

Организационно статистическая сводка может быть выполнена децентрализованно и централизованно.

При децентрализованной сводке материалы статистического наблюдения обрабатываются в несколько этапов в разрезе территориальных или административных единиц.

Например, децентрализованно обрабатываются данные статистической отчетности предприятий. Сводка начинается непосредственно на предприятиях, которые передают данные в местные статистические органы и региональные офисы предприятий, где они сводятся в масштабе округа (области, края, республики). Затем осуществляется сводка в масштабе субъекта Российской Федерации (округа) и, наконец, в целом по стране.

При такой организации сводки облегчается контроль полноты и достоверности данных, а также устранение ошибок, допущенных в статистических материалах, так как низовое структурное подразделение, приславшее материалы, находится близко от места обработки статистических данных и необходимые справки могут быть быстро получены.

Централизованная сводка осуществляется в одном месте, куда представляют данные наблюдения все отчетные единицы. Материалы единовременных обследований обрабатываются преимущественно централизованно.

Этот способ сводки обеспечивает единый подход в обработке всего материала и открывает более широкие возможности автоматизации счетных работ и применения информационных технологий в обработке результатов.

Таким образом, каждая форма сводки имеет свои преимущества и недостатки.

Децентрализованная сводка оказывается очень медленной, не обеспечивает всего комплекса группировок, очень трудоемка. Поэтому создаются автоматизированные системы обработки статистической информации в территориальных вычислительных центрах субъектов Российской Федерации. При таком способе обработки статистических данных предприятия направляют по сети Интернет в эти центры свои первичные данные для их сводки и группировки.