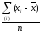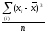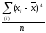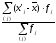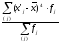- •1. Предмет и метод статистики
- •1.1 Возникновение и определение статистики
- •1.2. Предмет статистики и особенности статистики как науки
- •1.3. Статистические закономерности
- •1.4. Признаки
- •1.5. Метод статистики
- •1.6. Организация государственной статистики в рф
- •2. Средние величины
- •3. Статистическое наблюдение
- •3.1. Понятие статистического наблюдения. Этапы его проведения
- •3.2. Методологические вопросы статистического наблюдения
- •3.3. Основные организационные формы, виды и способы статистического наблюдения
- •Статистическое наблюдение
- •3.4. Статистическая отчетность
- •3.5. Требования, предъявляемые к данным стат. Наблюдения
- •3 Этап сн: подготовка данных к обработке
- •4. Вариационные ряды и их характеристика
- •4.1. Вариация массовых явлений
- •4.2. Построение вариационного ряда. Виды рядов. Ранжирование данных
- •4.3. Определение числа групп и величины интервала
- •4.4. Плотность распределения
- •4.5. Графическое изображение вариационного ряда
- •4.6. Структурные средние
- •Мода распределения
- •Медиана распределения
- •4.7. Другие структурные характеристики вариационного ряда Квартили и децили распределения
- •4.8. Показатели размера и интенсивности вариации
- •4.9. Свойства дисперсии и способы ее расчета
- •4.10. Дисперсия альтернативного признака
- •4.11. Виды дисперсий и правило их сложения
- •4.12. Закономерности распределения
- •4.13. Закон нормального распределения
- •4.14. Моменты распределения
- •4.15. Асимметрия распределения
- •4.16. Эксцесс распределения
- •5. Статистическая сводка. Группировка данных наблюдений. Таблицы
- •5.1. Статистическая сводка
- •5.2. Группировка данных
- •5.3. Определение числа групп и величины интервалов
- •5.4. Виды группировок
- •Типологические группировки
- •Структурные группировки
- •Аналитические группировки
- •5.5. Классификации
- •5.6. Сопоставимость статистических группировок
- •5.7. Статистические таблицы
- •6. Выборочное наблюдение и его организация
- •6.1. Выборочное наблюдение. Принципы теории выборки
- •6.2. Ошибки репрезентативности. Ошибки выборки
- •6.3. Определение необходимого объема выборки
- •6.4. Виды отбора единиц в выборочную совокупность
- •6.5. Малая выборка
- •6.6. Моментные наблюдения
- •7. Статистические показатели
- •7.1. Сущность статистических показателей
- •Границы объекта:
- •Статистический показатель
- •7.2. Классификация статистических показателей
- •7.3. Абсолютные показатели
- •7.4. Относительные показатели
- •8. Статистические методы изучения взаимосвязи между явлениями
- •8.1. Понятие корреляционной зависимости
- •8.2. Методы выявления корреляционной связи
- •Метод группировок
- •8.3. Изучение связи между двумя атрибутивными (качественными, описательными) признаками
- •8.4. Измерение связи по таблицам взаимной сопряженности
- •8.5. Измерение тесноты связи между порядковыми переменными
- •8.6. Показатели тесноты связи между двумя количественными признаками
- •Линейный коэффициент корреляции
- •8.7. Определение уравнения регрессии между двумя переменными
- •8.8. Теоретическое корреляционное отношение
- •8.9. Множественная корреляция
- •9. Ряды динамики
- •9.1. Понятие о рядах динамики. Их виды
- •9.2. Сопоставимость уровней ряда.
- •9.3. Основные показатели рядов динамики
- •Методы выявления основной тенденции в рядах динамики
- •Выявление и измерение сезонных колебаний
- •Измерение колеблемости в рядах динамики
- •Автокорреляция в рядах динамики
- •Определение уравнения авторегрессии
- •Элементы прогнозирования
- •10. Виды и способы построения индексов
- •10.1. Понятие об индексах. Их виды
- •10.2. Агрегатные индексы
- •1. Агрегатный индекс физического объема.
- •2. Агрегатный индекс цен
- •10.3. Средние индексы из индивидуальных
- •1. Индекс физического объема
- •2. Индекс цен
- •10.4. Индексы переменного и постоянного составов. Индекс структурных сдвигов
- •Iпост .
- •10.5. Цепные и базисные индексы
- •10.6. Определение роли отдельных факторов в динамике результативных показателей
- •10.7. Территориальные индексы
4.13. Закон нормального распределения
Закон нормального распределения характерен для распределения равновероятных событий, происходящих при взаимодействии множества случайных факторов.
Нормальное
распределение
характеризуется двумя существенными
параметрами, определяющими центр
группирования индивидуальных значений
и форму кривой: средней арифметической
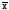 и средним квадратическим отклонением.
Кривые нормального распределения
различаются положением на оси абсцисс
центра распределения
и средним квадратическим отклонением.
Кривые нормального распределения
различаются положением на оси абсцисс
центра распределения
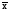 и разбросом вариант около этого центра
(рис. 4.1, 4.2).
и разбросом вариант около этого центра
(рис. 4.1, 4.2).
Нормальное распределение или закон Гаусса-Лапласа описывается уравнением
yt
=
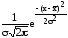 ,
,
где yt
– ордината кривой нормального
распределения, или частость (вероятность)
величины х нормального распределения;
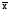 – математическое ожидание (среднее
значение) индивидуальных значений х.
– математическое ожидание (среднее
значение) индивидуальных значений х.
Если значения (х –
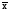 )
измерить (выразить) в величинах среднего
квадратического отклонения,
т.е. в стандартизованных (нормированных)
отклонениях t = (x –
)
измерить (выразить) в величинах среднего
квадратического отклонения,
т.е. в стандартизованных (нормированных)
отклонениях t = (x –
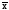 )/,
то формула примет вид yt
=
)/,
то формула примет вид yt
=
 .
.
Особенностью кривой
нормального распределения является ее
симметричность относительно центра
распределения – по обе стороны от ее
середины образуются две равномерно
убывающие ветви, асимптотически
приближающиеся к оси абсцисс. Поэтому
при нормальном распределении средняя,
мода и медиана совпадают:
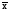 = Мо = Ме.
= Мо = Ме.
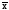 x
x
|
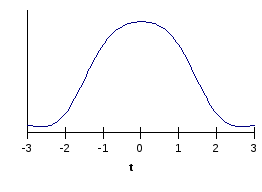
Рис. 4.1. Нормальное распределение |
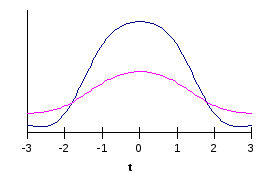
Рис. 4.2. Нормальное распределение с различными дисперсиями (12 < 22) |
Кривая нормального
распределения имеет две точки перегиба
(переход от выпуклости к вогнутости)
при отклонении вариантов от средней (х
–
 ),
равном среднему квадратическому
отклонению.
В пределах
),
равном среднему квадратическому
отклонению.
В пределах
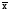
при нормальном распределении заключается
68,3%, в пределах
при нормальном распределении заключается
68,3%, в пределах
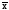 2
– 95,4%, в пределах
2
– 95,4%, в пределах
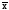 3
– 99,7% количества наблюдений или частот
ряда распределения. На практике почти
не встречаются отклонения, превышающие
3поэтому
приведенное соотношение называется
«правилом
трех сигм».
3
– 99,7% количества наблюдений или частот
ряда распределения. На практике почти
не встречаются отклонения, превышающие
3поэтому
приведенное соотношение называется
«правилом
трех сигм».
4.14. Моменты распределения
Средняя и дисперсия
это частные случаи более широкого
понятия обобщающих характеристик любого
распределения моментов.
Моментом распределения называется
средняя арифметическая тех или иных
степеней отклонений вариантов х от
некоторой постоянной величины А: z
=
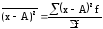 .
.
В зависимости от принятой величины А различают три вида моментов:
начальные
(при А=0)
 ,
,
центральные
(при
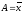 )
)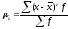 ,
,
условные
(при
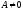 ,
,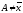 )
)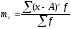 .
.
Как следует из формул моментов, начальный момент первого порядка представляет собой среднюю арифметическую.
Для дальнейшего изучения характера вариации используются средние значения разных степеней отклонений отдельных величин признака от его средней арифметической величины. Эти показатели получили название центральных моментов распределения.
Таблица
Центральные моменты
|
Порядок момента |
Формула | |
|
по несгруппированным данным |
по сгруппированным данным | |
|
Первый
(
Второй
(
Третий
(
Четвертый
(
|
|
|
Согласно свойству средней арифметической центральный момент первого порядка равен нулю, второй центральный момент представляет собой дисперсию. Величина третьего момента зависит, как и его знак, от преобладания положительных отклонений в кубе над отрицательными либо наоборот.
При нормальном и
любом другом строго симметричном
распределении сумма положительных
отклонений в кубе строго равна сумме
отрицательных отклонений в кубе (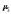 используется при оценке асимметрии).
Четвертый момент используется для
оценки эксцесса.
используется при оценке асимметрии).
Четвертый момент используется для
оценки эксцесса.
Условные моменты
самостоятельного значения не имеют,
ими пользуются для упрощения вычисления
центральных моментов:
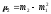 ,
,
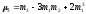 ,
,
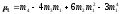 .
.
Рассмотренные нами ранее методы расчета средней арифметической и дисперсии способом отсчета от условного нуля или способом моментов свидетельствуют о существенном упрощении вычислительных операций.
Поскольку статистические характеристики наиболее часто рассчитываются для интервальных рядов распределения с равными интервалами, то отклонения х – А кратны величине интервала. Поэтому для исчисления условных моментов используется условная величина
m1
=
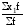 ;m2
=
;m2
=
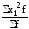 ;m3
=
;m3
=
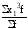 ;m4
=
;m4
=
 .
.
В этом случае центральные моменты корректируются на величину kz. Например:
2 = (m2 – m12)k2;
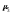 = (m3
– 3m1
m2
+ 2m13)k3.
= (m3
– 3m1
m2
+ 2m13)k3.

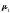 )
)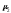 )
)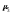 )
) )
)