4.9. Свойства дисперсии и способы ее расчета

В статистике наиболее часто мерой колеблемости признака служат дисперсия и среднее квадратическое отклонение. Дисперсия обладает рядом математических свойств, позволяющих упростить ее расчет.

1. Дисперсия постоянной величины равна нулю

2. Уменьшение всех значений признака на одну и ту же величину А не меняет величины дисперсии

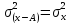
3. Уменьшение всех значений признака в к раз уменьшает дисперсию в к² раз

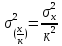
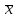4. Если вычислить дисперсию от любой величины А, в той или иной степени отличающейся от средней арифметической , то она всегда будет больше дисперсии, вычисленной от средней арифметической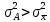

Дисперсия от А при этом будет больше на вполне определенную величину – на квадрат разности средней и величины А

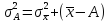или

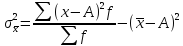
Из данного свойства следует важнейший вывод, что дисперсия от средней всегда меньше дисперсий от любых других величин, т.е. дисперсия от средней имеет свойство минимальности.

Если в последней формуле величину А приравнять к нулю, то получим

² = (x²f/f) – (xf/f)² = .

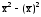Это упрощенный способ расчета дисперсии.

Это значит, что средний квадрат отклонений вариантов от средней величины равен среднему квадрату значений признака за вычетом квадрата среднего значения признака.

Кроме того, можно использовать для расчета дисперсии способ отсчета от условного нуля или способ моментов, который заключается в нахождении вариант, уменьшенных на условно постоянную величину А и в k раз, где k – интервал, т.е. х₁=(х – А)/k, и последующем расчете дисперсии по формуле

² .

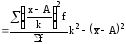Расчеты дисперсии различными способами дают одинаковые результаты, что позволяет исследователю выбрать наиболее эффективный способ.

4.10. Дисперсия альтернативного признака

В ряде случаев изучают не среднюю величину признака, а долю единиц, обладающих тем или иным признаком, например: долю прибыльных или убыточных подразделений предприятия, долю услуг, предоставленных с соблюдением или нарушением качества, и т.д.

Это примеры альтернативных вариаций, когда имеются лишь два взаимоисключающих варианта: наличие или отсутствие признака у данной единицы совокупности (1 наличие признака, 0 отсутствие). В таких случаях определяется дисперсия альтернативного признака.

Пусть доля единиц, обладающих данным признаком, равна р, а доля единиц, не обладающих этим признаком, 1–р, тогда 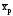=xf/f = [1∙p+0∙(1–p)]/(p+1–p) = p .

Естественно, средняя постоянной величины р есть сама эта величина, а дисперсия

²_p =  (x – 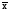)²f/f = [(1 – p)²p+(0 – p)²(1 – p)]/(p+1 – p) =

= (1 – p) p (1 – p+p)/1 = p(1 – p) ,

_p = .

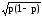Максимальное значение дисперсии альтернативного признака составляет 0,25 при р=0,5.

4.11. Виды дисперсий и правило их сложения

Для сгруппированной, т.е. разделенной на j групп, статистической совокупности можно вычислить три вида дисперсий:

• общую,

• внутригрупповые.

• межгрупповую.

Общая дисперсия характеризует колеблемость признака во всей изучаемой совокупности и определяется по формуле:

где x_i – значение признака i –й единицы совокупности,

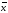- среднее значение признака в совокупности.

Для оценки колеблемости признака внутри каждой j –й группы вычисляют внутригрупповые дисперсии:

,

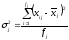где 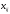- значение признака у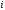-й единицы совокупности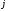-й группы,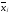- среднее значение признака в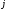- й группе,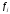- число единиц в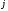- й группе.

Обобщенную характеристику внутригрупповой колеблемости вокруг групповых средних дает средняя величина из внутригрупповых дисперсий: .

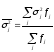Межгрупповая дисперсия показывает вариацию групповых средних вокруг средней величины признака в совокупности:

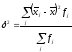
Между рассмотренными дисперсиями существует взаимосвязь, которая называется правилом сложения дисперсий: общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий.

.

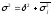Логика этого правила такова: общая вариация в совокупности складывается из вариации признака внутри отдельных групп и вариации между группами.