
- •1. Предмет и метод статистики
- •1.1 Возникновение и определение статистики
- •1.2. Предмет статистики и особенности статистики как науки
- •1.3. Статистические закономерности
- •1.4. Признаки
- •1.5. Метод статистики
- •1.6. Организация государственной статистики в рф
- •2. Средние величины
- •3. Статистическое наблюдение
- •3.1. Понятие статистического наблюдения. Этапы его проведения
- •3.2. Методологические вопросы статистического наблюдения
- •3.3. Основные организационные формы, виды и способы статистического наблюдения
- •Статистическое наблюдение
- •3.4. Статистическая отчетность
- •3.5. Требования, предъявляемые к данным стат. Наблюдения
- •3 Этап сн: подготовка данных к обработке
- •4. Вариационные ряды и их характеристика
- •4.1. Вариация массовых явлений
- •4.2. Построение вариационного ряда. Виды рядов. Ранжирование данных
- •4.3. Определение числа групп и величины интервала
- •4.4. Плотность распределения
- •4.5. Графическое изображение вариационного ряда
- •4.6. Структурные средние
- •Мода распределения
- •Медиана распределения
- •4.7. Другие структурные характеристики вариационного ряда Квартили и децили распределения
- •4.8. Показатели размера и интенсивности вариации
- •4.9. Свойства дисперсии и способы ее расчета
- •4.10. Дисперсия альтернативного признака
- •4.11. Виды дисперсий и правило их сложения
- •4.12. Закономерности распределения
- •4.13. Закон нормального распределения
- •4.14. Моменты распределения
- •4.15. Асимметрия распределения
- •4.16. Эксцесс распределения
- •5. Статистическая сводка. Группировка данных наблюдений. Таблицы
- •5.1. Статистическая сводка
- •5.2. Группировка данных
- •5.3. Определение числа групп и величины интервалов
- •5.4. Виды группировок
- •Типологические группировки
- •Структурные группировки
- •Аналитические группировки
- •5.5. Классификации
- •5.6. Сопоставимость статистических группировок
- •5.7. Статистические таблицы
- •6. Выборочное наблюдение и его организация
- •6.1. Выборочное наблюдение. Принципы теории выборки
- •6.2. Ошибки репрезентативности. Ошибки выборки
- •6.3. Определение необходимого объема выборки
- •6.4. Виды отбора единиц в выборочную совокупность
- •6.5. Малая выборка
- •6.6. Моментные наблюдения
- •7. Статистические показатели
- •7.1. Сущность статистических показателей
- •Границы объекта:
- •Статистический показатель
- •7.2. Классификация статистических показателей
- •7.3. Абсолютные показатели
- •7.4. Относительные показатели
- •8. Статистические методы изучения взаимосвязи между явлениями
- •8.1. Понятие корреляционной зависимости
- •8.2. Методы выявления корреляционной связи
- •Метод группировок
- •8.3. Изучение связи между двумя атрибутивными (качественными, описательными) признаками
- •8.4. Измерение связи по таблицам взаимной сопряженности
- •8.5. Измерение тесноты связи между порядковыми переменными
- •8.6. Показатели тесноты связи между двумя количественными признаками
- •Линейный коэффициент корреляции
- •8.7. Определение уравнения регрессии между двумя переменными
- •8.8. Теоретическое корреляционное отношение
- •8.9. Множественная корреляция
- •9. Ряды динамики
- •9.1. Понятие о рядах динамики. Их виды
- •9.2. Сопоставимость уровней ряда.
- •9.3. Основные показатели рядов динамики
- •Методы выявления основной тенденции в рядах динамики
- •Выявление и измерение сезонных колебаний
- •Измерение колеблемости в рядах динамики
- •Автокорреляция в рядах динамики
- •Определение уравнения авторегрессии
- •Элементы прогнозирования
- •10. Виды и способы построения индексов
- •10.1. Понятие об индексах. Их виды
- •10.2. Агрегатные индексы
- •1. Агрегатный индекс физического объема.
- •2. Агрегатный индекс цен
- •10.3. Средние индексы из индивидуальных
- •1. Индекс физического объема
- •2. Индекс цен
- •10.4. Индексы переменного и постоянного составов. Индекс структурных сдвигов
- •Iпост .
- •10.5. Цепные и базисные индексы
- •10.6. Определение роли отдельных факторов в динамике результативных показателей
- •10.7. Территориальные индексы
4.7. Другие структурные характеристики вариационного ряда Квартили и децили распределения
Квартили – это значения признака, делящие ранжированный ряд на четыре равновеликие части. Первый квартиль (Q1) определяет ¼ часть совокупности с наименьшими значениями признака, третий квартиль(Q3) отсекает ¼ часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1, 25% единиц заключены между Q1 и Q2, 25% – между Q2 и Q3, остальные 25% превосходят Q3. Вторым квартилем является медиана. Для расчета квартилей в интервальном вариационном ряду применяют формулы:
Q1
=
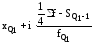 ,Q3
=
,Q3
=
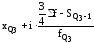 ,
,
где
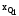 ,
,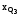 – нижняя граница интервала, содержащего
первый, третий квартиль (интервал
определяется по накопленной частоте,
первой превышающей 25%, 75%);i
– величина интервала;
– нижняя граница интервала, содержащего
первый, третий квартиль (интервал
определяется по накопленной частоте,
первой превышающей 25%, 75%);i
– величина интервала;
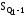 ,
,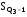 – накопленная частота интервала,
предшествующего интервалу, содержащему
первый, третий квартиль;
– накопленная частота интервала,
предшествующего интервалу, содержащему
первый, третий квартиль;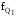 ,
,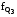 – частота интервала, содержащего первый,
третий квартиль.
– частота интервала, содержащего первый,
третий квартиль.
Децили – варианты, делящие ранжированный ряд на десять равных частей. Первый дециль (d1) делит совокупность в соотношении 1/10 к 9/10, второй дециль (d2) – в соотношении 2/10 к 8/10 и т.д. Расчет децилей осуществляется по той же схеме, что и медиана и квартили:
D1
=
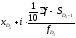 ,D2
=
,D2
=
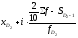 .
.
В социально-экономических исследованиях часто используется коэффициент децильной дифференциации
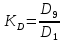
Значения признака, делящие ряд на сто частей, называются перцентилями.
4.8. Показатели размера и интенсивности вариации
Средняя величина, давая обобщающую характеристику вариационного ряда, не показывает, как располагаются около нее варианты признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. А от размера и распределения отклонений вариант зависят типичность и надежность средних характеристик
Следовательно, при характеристике вариационных рядов средние должны быть дополнены показателями вариации, измеряющими отклонения признаков от средней.
Вариация - различие значений признака у отдельных единиц совокупности в один и тот же период или момент времени.
Вариация вызвана воздействием каких-либо факторов на социально-экономические явления или процессы, причем характер этого воздействия определяет характер колеблемости, изменчивости признака. Поэтому анализ показателей вариации позволяет оценить влияние факторов и условий на изменчивость признаков.
Вариация прибыли и рентабельности предприятий обусловлена широким кругом внешних и внутренних факторов. Анализируя вариацию, мы можем определить доминирующие факторы. Например, на предприятиях с минимальной рентабельностью – узкие места, на предприятиях с максимальной рентабельностью – изучение опыта.
Статистический анализ вариации включает:
построение вариационного ряда
графическое изображение ряда
расчет показателей центра распределения и структурных характеристик вариационного ряда
расчет показателей размера и интенсивности вариации
оценка вариационного ряда на асимметрию и эксцесс.
Абсолютные показатели вариации
Наиболее простой характеристикой вариации является размах вариации, исчисляемый разностью между наибольшим и наименьшим значениями варьирующего признака:
R = xmax–xmin.
Этот показатель дает самое общее представление о колеблемости признака, его значение определяется только двумя крайними значениями, тогда как колеблемость признака в целом складывается из всех значений совокупности. Размах вариации предназначен для измерения колеблемости признаков в совокупностях с небольшой численностью единиц.
Для характеристики вариации необходимо знать не только размах значений признака, но и обобщенные (суммарные) отклонения всех значений признака от какого-то типичного для изучаемой совокупности значения. В качестве такового обычно используется средняя арифметическая.
Характеристика
вариации признака на основе отклонений
его значений от средней может быть дана
с помощью среднего
линейного отклонения,
рассчитываемого на основе абсолютных
отклонений вариантов от их средней:
l
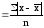 ,l
,l
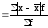 .
.
Первая формула применяется для несистематизированных данных, вторая – в вариационных рядах.
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней арифметической:
простая дисперсия
2
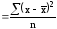 ;
;
взвешенная дисперсия
2
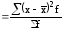 .
.
Корень квадратный из дисперсии представляет собой среднее квадратическое отклонение:
=
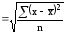 ;
=
;
=
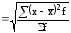 .
.
Размах вариации, среднее квадратическое отклонение, среднее линейное отклонение измеряет абсолютную меру колеблемости признака и выражается в тех же единицах измерения, что и варианты. Дисперсия единицы измерения не имеет.
В зарубежной статистической практике среднее квадратическое отклонение называется стандартным отклонением и применяется в различных стандартах.
Еще одним показателем силы вариации, характеризующим ее не по всей совокупности, а лишь в центральной части, служит среднее квартильное расстояние, т.е. средняя величина разности между квартилями:
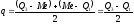
Относительные показатели вариации
Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем более для разных признаков необходимы относительные показатели вариации. Они вычисляются как отношения абсолютных показателей силы вариации, рассмотренных ранее, к средней арифметической величине признака.
Т.о. получаем следующие относительные показатели вариации:
1. относительный
размах вариации (коэффициент осцилляции)
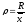 ,
,
2. относительное
отклонение по модулю (коэффициент
вариации по среднему линейному отклонению,
линейный коэффициент вариации)
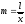 ,
,
3. коэффициент
вариации (коэффициент вариации по
среднему квадратическому отклонению)
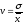 .
.
Коэффициент вариации по среднему квадратическому отклонению в статистике играет важную роль. Из теории математической статистики известно, что можно говорить об однородности изучаемой совокупности, если выдерживается неравенство
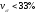
|
Коэффициент вариации, % |
Степень однородности совокупности |
|
Менее 30 |
однородная |
|
30 - 60 |
средняя |
|
60 и более |
неоднородная |
Поэтому коэффициент вариации по среднему квадратическому отклонению является критерием типичности средней и однородности совокупности.
4. относительное
квартильное расстояние
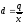 .
.
