4.6. Структурные средние

Помимо степенных средних в статистике связи также используются структурные средние: мода, медиана.

Являясь важнейшей обобщающей характеристикой вариационного ряда степенная средняя величина характеризует центр распределения.

Вспомним важнейшее свойство средней: (x–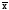)f = 0. Т.е. в средней величине индивидуальные отклонения единиц совокупности от средней взаимопогашаются – проявление закона больших чисел.

Однако значение средней может не совпадать ни с одной из реально существующих вариант, например, средний тарифный разряд равен 3,6, хотя разряд рабочего не может быть дробным числом. Поэтому наряду со средней для анализа рядов распределения целесообразно применять значения конкретных вариант, которые в упорядоченном ряду занимают определенное положение. К таким значениям относятся модаимедиана, называемые структурными средними рядов распределения.

Мода распределения

В вариационном ряду модой является вариант, обладающий наибольшей частотой или частостью. Этот показатель применяется в тех случаях, когда необходимо охарактеризовать наиболее часто встречающееся значение признака, наиболее распространенный вид услуг связи, преобладающую форму организации труда, типичную конфигурации информационных и телекоммуникационных сетей.

В ряде случаев мода является более эффективной характеристикой, чем средняя. Например, при оценке качества предоставления услуг, надежности работы технических средств распределение единиц совокупности в этих рядах имеет асимметрию, сдвиг влево или вправо от центра распределения, поэтому типичной характеристикой является не средняя, а мода как наиболее часто встречающееся значение показателя.

В дискретных рядах моду находят очень просто по наибольшей частоте. Так, в приведенном в таблице 4.1 распределении работников по тарифному разряду наиболее распространенным является 4-й разряд как наиболее часто встречающийся.

Обычно встречаются ряды с одним модальным значением признака. Если два или несколько (и даже несколько различных, но больших, чем соседние) значений признака имеются в вариационном ряду, он считается соответственно бимодальным или мультимодальным. Это говорит о неоднородности совокупности.

В интервальном вариационном ряду, тем более при непрерывной вариации признака, строго говоря, каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака - точечную моду.

Т.о. в интервальном ряду с равными интервалами мода рассчитывается на основе интерполяции модального интервала по следующей формуле: Mo = x_Mo + i ,

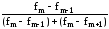где х_Мо – начальная граница модального интервала;

i – величина модального интервала;

f_m-1, f_m, f_m+1 – частоты интервалов предшествующего модальному, модального и следующего за модальным.

Мода в рядах с неравными интервалами определяется через плотности распределения (абсолютные или относительные): Mo = x_Mo + i ,

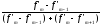Медиана распределения

Медианой является вариант, делящий численность вариационного ряда на две равные части. Другими словами, этот вариант расположен в середине ранжированного ряда, при этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой больше.

Главное свойство медианы: сумма отклонений вариант от медианы по модулю меньше, чем от любой другой величины

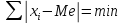
Для определения медианы в ранжированных рядах необходимо придать всем единицам ряда порядковые номера.

В рядах с нечетным количеством членов ряда медианой является значение признака члена ряда, имеющего порядковый номер середины ряда (n+1)/2.

Например, в ряду с количеством членов ряда 101 номер медианной варианты 51-й: (101+1)/2=51, т.е. медианой является вариант, стоящий в середине ряда, с номером 51.

В рядах с четным числом членов ряда медианой является среднее значение признака двух вариантов, имеющих номера n/2 и n/2+1.

Так, если в ряду 100 членов ряда, то медианой является среднее значение признака 2-х вариант: 50-й и 51-й.

Однако в рядах с большим числом единиц совокупности и незначительным различием в значениях рядом стоящих вариантов медианой обычно считается значение признака варианты с порядковым номером n/2 (чтобы медианой было значение признака конкретной варианты).

Определение медианы в дискретном ряду.

Медианой в дискретном ряду считают значение признака в той группе, в которой накопленная частота (частость) первая превышает половину численности ряда ().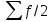

Нахождению медианы в интервальном ряду предшествует определение медианного интервала, накопленная (кумулятивная) частота которого равна или превышает полусумму всех частот ряда. Затем медиана рассчитывается по формуле Ме = х_Me + i ,

где х_Me – начальная граница медианного интервала;

i – величина медианного интервала;

f – численность ряда;

S_m-1 – сумма накопленных частот интервалов, предшествующих медианному;

f_m – частота медианного интервала.

В зависимости от цели исследования, свойств и закономерности распределения совокупности могут использоваться либо одна из обобщающих характеристик: средняя, мода, медиана, либо для сравнения – все три. Для средней арифметической характерно, что все отклонения от неё в сумме дают нуль, для медианы – сумма отклонений от неё по модулю является минимальной, мода представляет собой значение признака, которое наиболее часто встречается.