4.5. Графическое изображение вариационного ряда

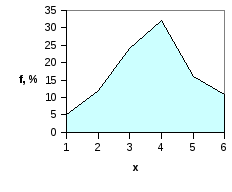
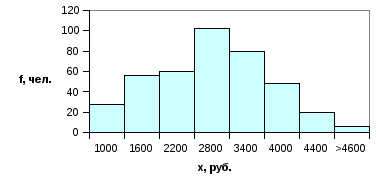
Простейшим методом анализа рядов распределения является их графическое изображение, позволяющее раскрыть характер распределения единиц совокупности при изменении варьирующего признака, сопоставить несколько рядов и сравнить с теоретическим распределением. Вариационные ряды наглядно представляются в виде полигона и гистограммы распределения.

Полигон и гистограмма распределения являются графическим представлением вариационного ряда распределения. Полигон и гистограмма одинаковы по назначению и сходны по принципам построения: на оси абсцисс откладываются значения вариантов х, на оси ординат частоты или плотности распределения f. Различие между ними заключается в способе обозначения частот. На полигоне частоты отмечаются точками, ориентированными по обеим осям координат, полученные точки соединяются отрезками прямой и образуют эмпирическую кривую распределения – график зависимости частоты или плотности распределения от значения признака. На гистограмме частоты выражаются высотой прямоугольников, построенных на отрезках оси абсцисс, ширина прямоугольников равна величине интервала. Если середины верхних сторон прямоугольников, соответствующие серединам интервалов, соединить отрезками прямой линии, то гистограмма преобразуется в полигон распределения. На рис. Г.13 изображен полигон распределения рабочих связи по тарифному разряду (дискретный ряд), на рис. Г.14 полигон и гистограмма распределения работников связи по размеру заработной платы (интервальный ряд).

Рис. Г.13. Полигон распределения (f) рабочих связи по тарифному разряду (х)

Рис. Г.14. Полигон (1) и гистограмма (2) распределения работников связи (f) по размеру заработной платы (х)

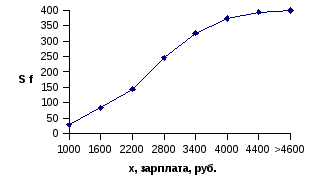
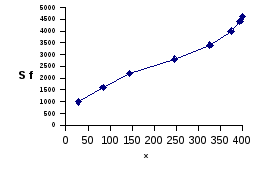
С помощью графического изображения рядов в виде полигона и гистограммы можно сравнивать распределение единиц совокупности по различным признакам. Такое сравнение облегчается построением кумуляты или огивы распределения (кривых накопленных сумм). Они удобны для анализа характера и сопоставления различных рядов распределения, что особенно важно при многофакторном анализе социально-экономических явлений.

Кумулята и огива распределения являются графическим отражением вариационного ряда распределния. Кумулята, или кривая сумм, строится по накопленным частотам, т.е. на оси ординат откладываются нарастающие итоги частот (рис.Г.7,а). Если на оси ординат отложить данные вариантов, а на оси абсцисс накопленные частоты, то получим огиву график, обратный кумуляте (рис. Г.7,б). Кумулята характеризуется монотонным возрастанием, причем изменение накопленных частот имеет определенную закономерность: сначала они возрастают медленно, затем ускоренно, в конце снова резко замедляют темп изменения до достижения конечной точки, равной количеству единиц изучаемой совокупности. Такая закономерность типична для нормального закона распределения, который характеризуется преобладанием частот со средним уровнем признака и их незначительным количеством с крайними значениями (минимальным и максимальным) признаков.

а) б)

Рис. Г.7. Кумулята (а) и огива (б) распределения работников связи

по уровню заработной платы