4.3. Определение числа групп и величины интервала

Число групп в дискретном вариационном ряду определяется числом реально существующих значений варьирующего признака. Если признак принимает дискретные значения, но их число очень велико (например, численность работников на 1 января в разных предприятиях отрасли), то строится интервальный вариационный ряд.

Интервальный вариационный ряд строится и для изучения непрерывных признаков, которые могут принимать любые, как целые, так и дробные значения. Например, доход на 1 жителя, рентабельность предприятия, все вторичные признаки, значения которых рассчитываются путем деления величины одного первичного признака на величину другого.

Интервальные вариационные ряды бывают

1. с равными интервалами,

2. с неравными интервалами.

Наиболее часто используются два вида интервальных вариационных рядов: равноинтервальный и равночастотный.

Равноинервальный ряд применяется, если вариация признака не очень сильна, т.е. для однородной совокупности, распределение которой по данному признаку близко к нормальному закону. Ряд с неравными интервалами и в частности равночастотный ряд применяется, если вариация признака очень сильна.

При построении равноинтервального ряда число групп выбирается так, чтобы в достаточной мере отразились разнообразие значений признака в совокупности и в то же время закономерность распределения, а его форма не искажалась случайными колебаниями частот. Если групп слишком мало, не проявится закономерность вариации; если групп будет слишком много, случайные скачки частот исказят форму распределения.

Чаще всего число групп в вариационном ряду определяют по формуле американского статистика Стерджесса:

,

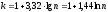где 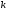- число групп,- число единиц совокупности.

Зная число групп, можно определить величину интервала: .

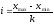Равночастотный вариационный ряд необходим при очень сильной вариации признака потому, что при равноинтервальном распределении большая часть единиц совокупности окажется в крайней группе (первой или последней). Часть групп не будет включать ни одной единицы совокупности. Число групп равночастотного ряда часто принимают равным 10, т.е. в каждой группе содержится 10% единиц совокупности. Такие группы называют децильными. Так, например, группируют домохозяйства по данным выборочного бюджетного обследования доходов населения России и субъектов федерации органы Госкомстата. Децильные группы применяются также для изучения распределения банков, промышленных компаний по размерам их активов или собственного капитала.

4.4. Плотность распределения

Частоты интервальных вариационных рядов зависят от характера распределения единиц совокупности и величины интервала. Частота будет тем больше, чем шире интервал. Поэтому при неравных интервалах частоты не дают представления о характере распределения и непосредственно несопоставимы.

Если мы имеем дело с вариационным рядом с неравными интервалами, то для сопоставимости нужно частоты, или частости, привести к единице интервала. Полученное отношение называется плотностью распределения:

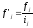или ,

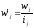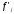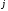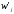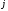где - абсолютная плотность распределения в-м интервале;- относительная плотность распределения в-м интервале;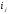- ширин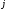а-го интервала.