3 Этап сн: подготовка данных к обработке
Ошибки наблюдения (регистрации) выявляются при хорошей организации статистического контроля. После получения статистических формуляров следует прежде всего провести проверку полноты собранных данных, т.е. определить, все ли отчетные единицы заполнили статистические формуляры и значения всех ли показателей отражены в них.
Следующим этапом контроля точности информации является арифметический контроль. Он основывается на использовании количественных взаимосвязей между различными показателями. Если арифметический контроль показывает, что количественная зависимость не выполняется, это свидетельствует о недостоверности собранных данных. Поэтому в программу статистического наблюдения целесообразно включать показатели, которые дают возможность провести арифметический контроль, для этой же цели в формуляры включаются контрольные суммы.
Логический контроль, также как и арифметический, основывается на знании взаимосвязей между показателями, но не количественных, а логических. Например, человек в возрасте 6 лет не может иметь среднего образования. Поэтому если в бланке переписи имеются обе записи, то это показывает, что одна из них не соответствует действительности.
4. Вариационные ряды и их характеристика
4.1. Вариация массовых явлений
Вариацией значений какого-либо признака в совокупности называется его различие его значений у разных единиц данной совокупности в один и тот же период или момент времени.
В отличие от вариации значений признака у разных единиц совокупности, различие значений признака у одной и той же единицы совокупности в разные периоды или моменты времени следует называть изменениями или колебаниями во времени. Методы их изучения и измерения принципиально отличаются от методов измерения вариации.
Причиной вариации являются разные условия существования разных единиц совокупности. Вариация присуща всем без исключения явлениям природы и общества, кроме законодательно закрепленных нормативных значений отдельных социальных признаков: не варьирует признак «число президентов, премьер-министров страны». Неварьирующие признаки не представляют интереса для статистики; предметом изучения статистики является вариация.
Для изучения вариации статистикой разработаны специальные методы исследования, система показателей, с помощью которой вариация измеряется, характеризуются ее свойства.
4.2. Построение вариационного ряда. Виды рядов. Ранжирование данных
Первым этапом статистического изучения вариации является построение вариационного ряда – упорядочение единиц совокупности по возрастающим или по убывающим значениям признака и подсчет числа единиц с тем или иным значением признака.
Ряды распределения характеризуются двумя основными элементами:
вариантами х, т.е. отдельными значениями группировочного признака,
частотами f , представляющими собой количество тех или иных вариант, встречающих в данной совокупности.
Существует три формы вариационного рядя:
ранжированный,
дискретный,
интервальный.
Вариационный ряд часто называют рядом распределения (распределения частот при изменении вариант). Ряд распределения представляет собой структурную группировку.
Ранжированный ряд – это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.
Если численность единиц совокупности достаточно велика, ранжированный ряд становится громоздким. В таких случаях вариационный ряд строится с помощью группировки единиц совокупности по значениям изучаемого признака, т.е. осуществляется подсчет единиц с тем или иным значением признака.
Если признак принимает небольшое число значений, строится дискретный вариационный ряд.
Таблица 4.1
Распределение работников предприятия по тарифному разряду
|
Тарифный разряд |
1 |
2 |
3 |
4 |
5 |
6 |
Итого |
|
Численность, чел |
25 |
60 |
120 |
160 |
80 |
55 |
500 |
Дискретный
вариационный ряд
– это таблица, состоящая из двух строк
или граф: конкретных значений варьирующего
признака
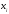и числа единиц совокупности с данным
значением признака
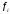- частот (или долей этого числа в общей
численности совокупности (частостей)).
Частость –
относительное выражение частоты
Интервальный вариационный ряд - это таблица, состоящая из двух строк или граф – интервалов признака, вариация которого изучается, и числа единиц совокупности, попадающих в данный интервал (частот), или долей этого числа от общей численности совокупности (частостей).
В интервальных рядах частоты относятся не к отдельному значению признака, как в дискретных рядах, а ко всему интервалу.