5.0. Гармонический источник. Представление схемы электрической цепи схемой квазипостоянных токов в комплексной системе представления

5.1. Понятие гармонической функции

Из всего множества гармонических функций, выделим тригонометрические гармонические функции и определим их специфику по отношению к общему определению рассматриваемых функций следующим образом:

• область независимой переменной принадлежит множеству действительных чисел на всей числовой оси ± ∞;

• область значений функции также лежит в в пределах ± ∞;

• в качестве независимой переменной используется время.

Функцию запишем в виде

u(t)=U_m SIN(2πf t) или u(t)= U_m COS(2πf t),

где U_m – постоянная, называемая амплитудой гармонической функции, f– постоянная, в данном случае её размерность с^-1. Эта постоянная носит название частоты, например, максимума данной функции на интервале времени 1с. Произведение 2πf есть также частота оборотов вектора длиной U_m в течении 1с. Принятое обозначение ω = 2πf.

Поскольку конкретность рассмотрения интервалов времени не может находиться на -∞, то для рассматриваемого интервала времени, в течении которого происходит применение данной функции вводят начало интервала принимаемого часто за нуль. Для того, чтобы сохранить непрерывность гармонической функции, в момент времени, принимаемого за нуль, вводят произвольное значение u(0). Соответствующее такому значению функции значение аргумента называют начальной фазой гармонической функции. В этом случае формула принимает вид

u(t)= U_m SIN(2πf t ±ψ) или u(t)= COS(2πf t ±ψ).

Здесь ψ обозначение начальной фазы.

3. Развитие модельных представлений в теории цепей. Операторный метод. Анализ переходного процесса в последовательном rlc-примитиве. Переходные характеристики

Рассмотрим схему последовательного RLC контура в операторной области

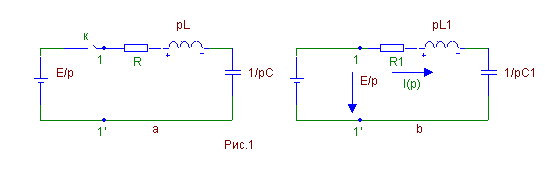
На рис.1а показана схема с разомкнутым ключом «К», а на рис.1б эта же цепь после замыкания ключа.

Момент времени замыкания ключа обозначим через 0 и составим выражение для тока I(р), определив его как отношение напряжения на узлах 1,1' к величине входного сопротивления цепи на этих же узлах.

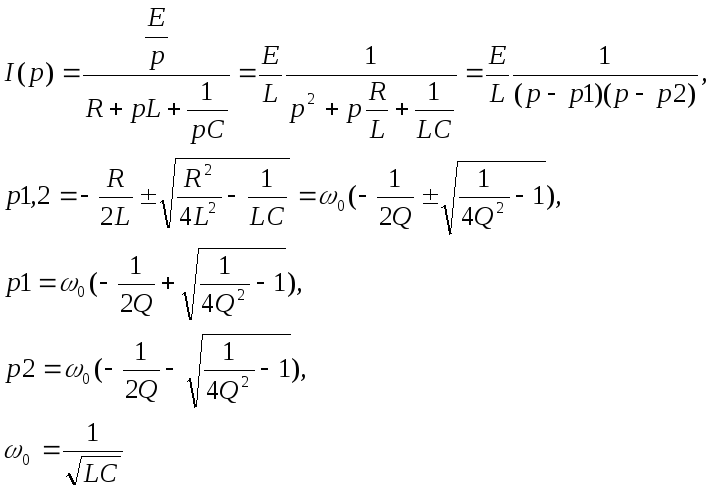(3.1)

Обратное преобразование из операторной области во временную получим из таблиц перехода

. (3.2)

Поскольку возможно три различных значений каждого корня, то формул для тока будет также три.

1. В случае 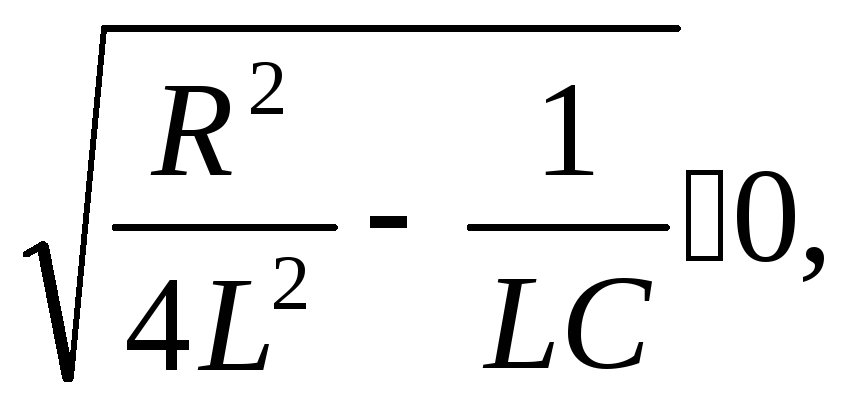каждый из корней есть действительное число. Это случай корней действительных и разных. Выражение для тока во временной области будет представлено формулой

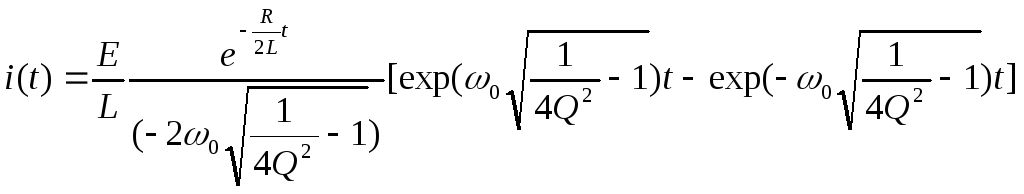(3.3)

2. В случае 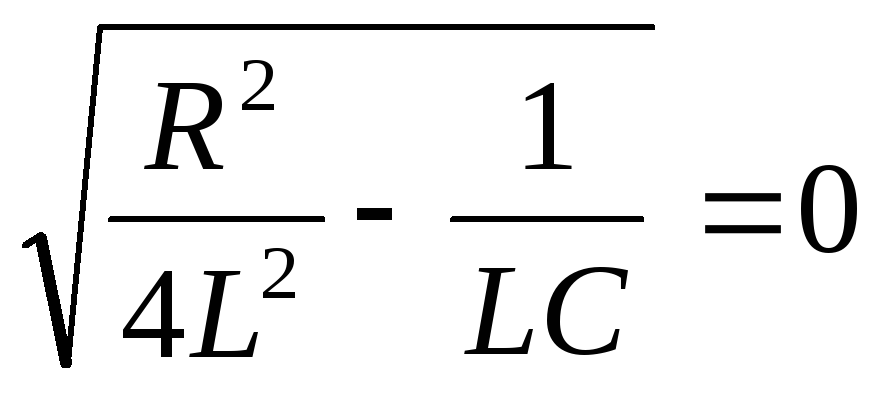, р1=р2=-R/2L. Это случай корней действительных и равных. Выражение для тока во временной области будет представлено несколько другой формулой, т.к. (3.2) в данном случае представимо отношением 0/0. После применения правила Лапиталя (p1=const‚ p2=var), ток во временной области выразим формулой

. (3.4)

3. В случае 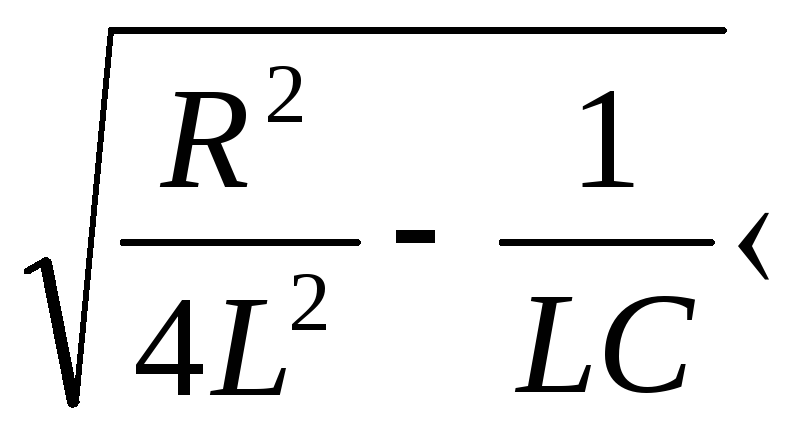0, получаем два комплексно-сопряжённых корня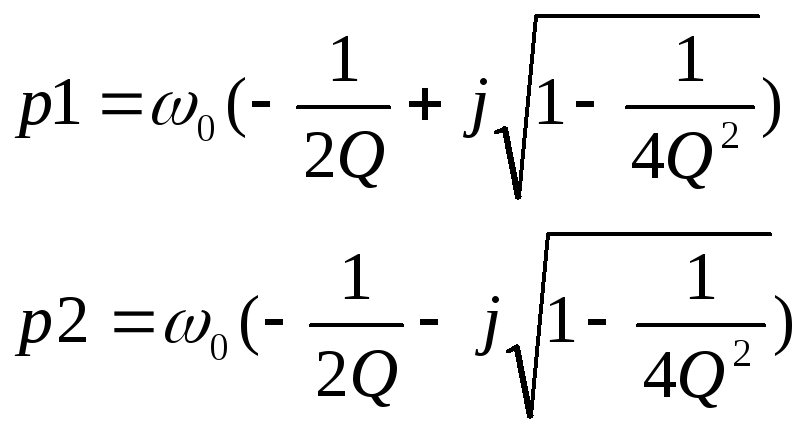,(3.5)

и формула тока может быть представлена выражением

(3.6)

Найдём характерные точки кривых (точка экстремумов, точки перехода через нуль), соответствующих трём рассмотренным случаям.

Случай корней действительных и разных.

Определим момент времени, при котором кривая имеет максимум:

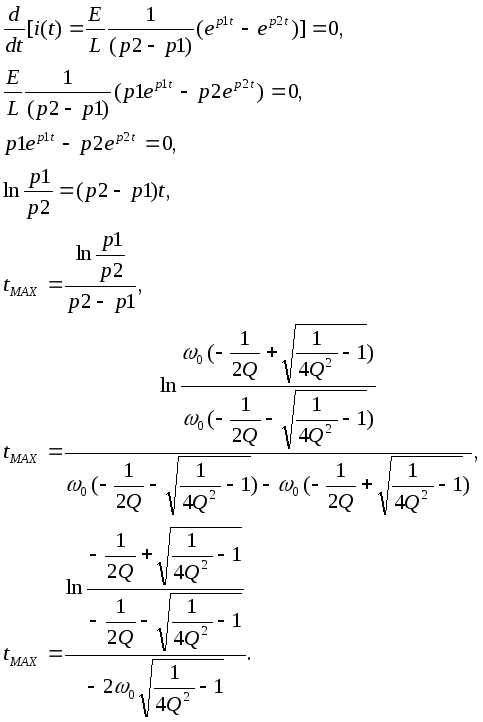(3.7)

Значение должно быть действительным положительным числом. В рассматриваемом случае Q < 0,5. Следовательно, в выражении под логарифмом числитель меньше чем знаменатель, и оба они отрицательные числа. Логарифм также будет иметь отрицательное значение. Отрицательным является также и знаменатель всего выражения.

Таким образом, получаем величину момента времени больше нуля.

График функции тока будет иметь один максимум.

Случай корней действительных и равных.

Определим момент времени, при котором кривая имеет максимум:

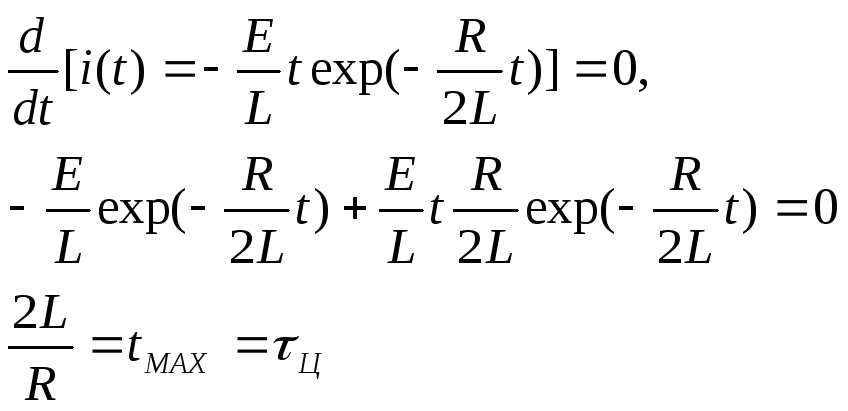(3.8)

Случай корней комплексно-сопряжённых.

Определим момент времени, при котором кривая имеет максимум:

(3.9)

Характер выражения (3.6) указывает на то, что график будет представлять импульс в виде затухающей «синусоиды». Поэтому полученное выражение определяет расстояние от начала графика, и этому значению будет соответствовать максимальная амплитуда, среди всех других амплитуд полупериодов затухающей «синусоиды».

Напряжение на выходе RLC-четырёхполюсника. Переходная характеристика

Очевидно, что величина тока, характер функции i1,1'(t) не изменяться при перестановке элементов R,L,C в рассматриваемом контуре, поэтому три полученных функций тока исчерпывают возможные решения.

Если будем рассматривать напряжение на узлах 2,2', то в зависимости от того, какой элемент из перечисленных находится между этими узлами, функция напряжения будет различной при одной и той же функции тока.

Таким образом, для каждого элемента будем иметь три различные функции, представляющие напряжение на указанных узлах.

Поскольку таких элементов в рассматриваемой цепи также три, то общее число функций, представляющих множество напряжений, равно девяти.

Формирование множества напряжений будем производить таким образом: для каждого варианта схемы рассмотрим возможные функции напряжения, используя три известные функции тока.

Возможные варианты напряжения на узлах 2,2, если элементом выхода является резистивный элемент

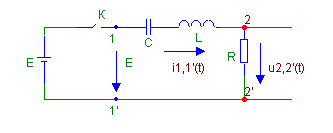
Рис.

Пусть добротность контура меньше 0,5. Это означает, что ток i1,1'(t) будет представлять собой после замыкания ключа К экспоненциальный импульс в соответствии с (3.6).

Напряжение на узлах 2,2' найдём по формуле u_2,2'(t) = Ri_1,1'(t):

. (3,10)

Видно, что характер функции напряжения не изменяется по сравнению с функцией тока т.к. R есть положительное вещественное число.

При t = 0 напряжение на выходе равняется нулю. Объясним это состояние на основе законов коммутации.

В момент замыкания ключа К (этот момент времени примем за нуль) на узлах 1,1' напряжение скачком изменилось до величины К, но ток остаётся равным нулю. Для индуктивного элемента закон коммутации для тока (ток скачком измениться не может) имеет вид

i_L(t_0-)= i_L(t₀)= i_L(t₀₊),

а т.к. в схеме последовательное соединение , то такой же ток имеет место и для каждого другого элемента. Поскольку при t<0 ток был равен нулю, то и в момент t=0 ток равен нулю, поэтому напряжение на R также равно нулю.

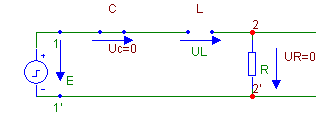
Рис.

Это же подтверждает и формула (3.10), если подставить значение t=0.

Очевидно, что при t→∞, выражение обращается в нуль. Объяснение также построим на применении метода эквивалентных схем.

При t>0 схема может быть представлена эквивалентной схемой.

Источник напряжения представляем источником постоянного напряжения и при t→∞ емкостной элемент может быть представлен элементом типа «разрыв», а индуктивный – элементом типа «короткое замыкание». Ток в цепи отсутствует и напряжение на R равно нулю.

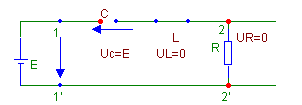
Рис.

Обратимся к случаю, когда добротность контура равна 0,5. Напряжение на узлах 2,2' можно определить в соответствии с приведенной выше формулой, используя выражение тока для корней действительных и равных:

. (3.11)

При t=0 напряжение равно нулю. Про t→∞ напряжение также стремиться к нулю. Объяснить это можно также, как это было сделано выше.

И, наконец, третий случай – добротность более 0,5:

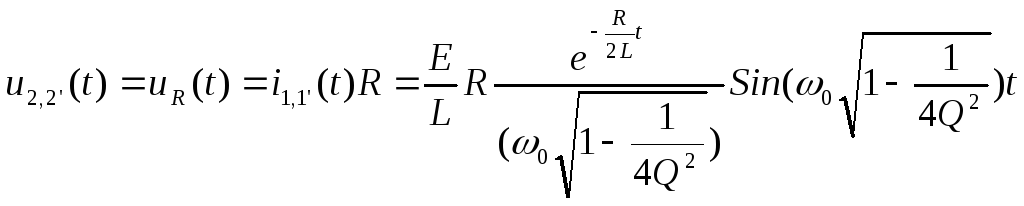. (3.12)

При t=0 и t→∞ напряжение нулевое. Пояснения теже.

Возможные варианты напряжения на узлах 2,2, если элементом выхода является индуктивный элемент

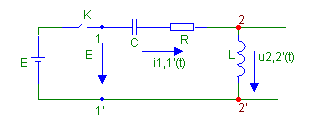
Рис.

Имея выражение для тока, напряжение на индуктивном элементе можно найти по формуле

Q<0,5

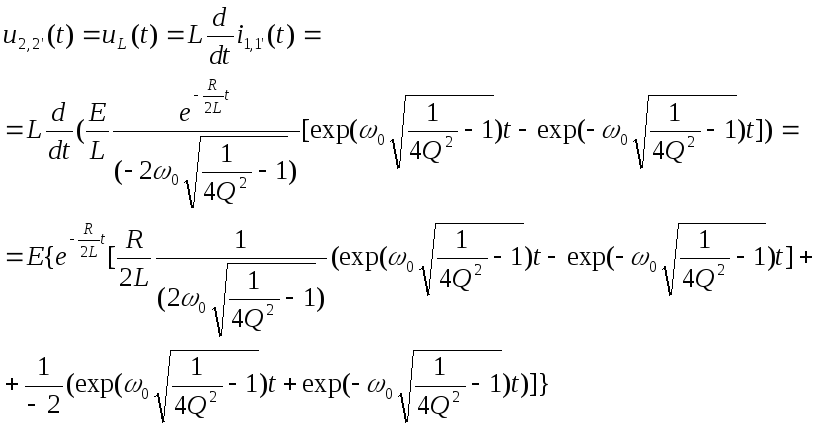(3.13)

Рассмотрим крайние случаи. При t=0 напряжение на индуктивном элементе скачком меняется и делается равным E, а при t → ∞ стремится к нулю.

Первое объясняется законами коммутации: напряжение на индуктивном элементе может измениться скачком, а ток не может измениться скачком, если изменяется напряжение скачком, в данном случае, на входе цепи

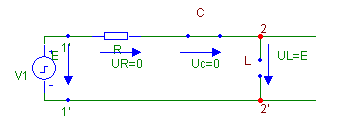
Рис.

i_L(t_0-)= i_L(t₀)= i_L(t₀₊)=0.

Второе- тем, что при t>0 цепь находится под воздействием источника постоянного напряжения и при t→∞ цепь переходит в стационарное состояние и элемент L можно заменить эквивалентным элементом типа «короткое замыкание»,

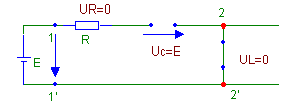
Рис.

элемент С – эквивалентом типа «разрыв».

Q = 0,5

Это случай корней действительных и равных.

Напряжение на узлах 2,2' определим по формуле

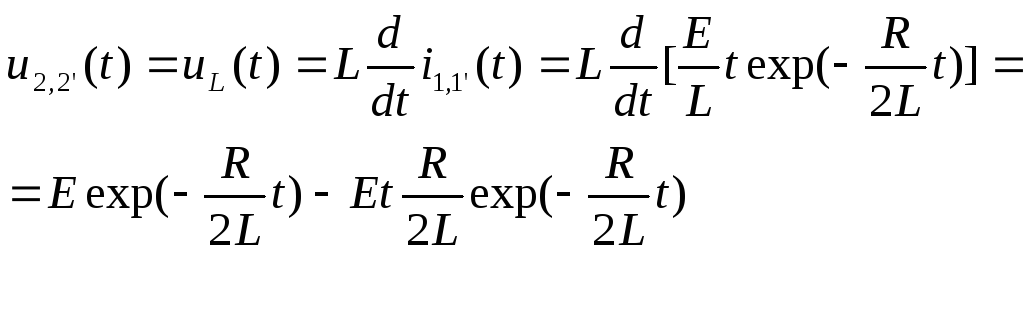(3.14)

Из формулы видно, что при t=0 напряжение на узлах 2,2' изменяется скачком, а при t→∞ стремится к нулю.

Объяснение аналогично рассмотренному выше.

Q > 0,5

Случай корней комплексно-сопрояжённых

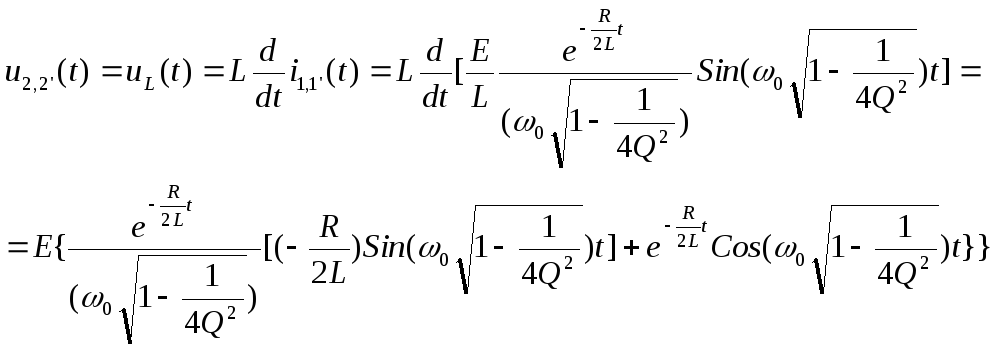(3.15)

Из формулы видно, что при t=0 напряжение на узлах 2,2' изменяется скачком, а при t→∞ стремится к нулю.

Объяснение аналогично рассмотренному выше.

Возможные варианты напряжения на узлах 2,2, если элементом выхода является емкостной элемент

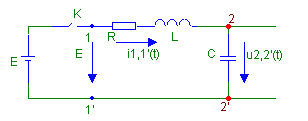
Рис.

В данном случае можно поступить как и в предыдущих двух - использовать оператор связи между током и напряжением, заданными как функции времени. Однако, интегрирование создаст большее число необходимых алгебраических операций для приведения формул к виду удобному для непосредственного анализа.

В выражении (3.1) имеется операторное представление для тока, которое можно использовать для получения напряжения на элементе С на основе произведения

,

из которого, применив таблицы перехода, перейдём во временную область.

Случай корней действительных и разных

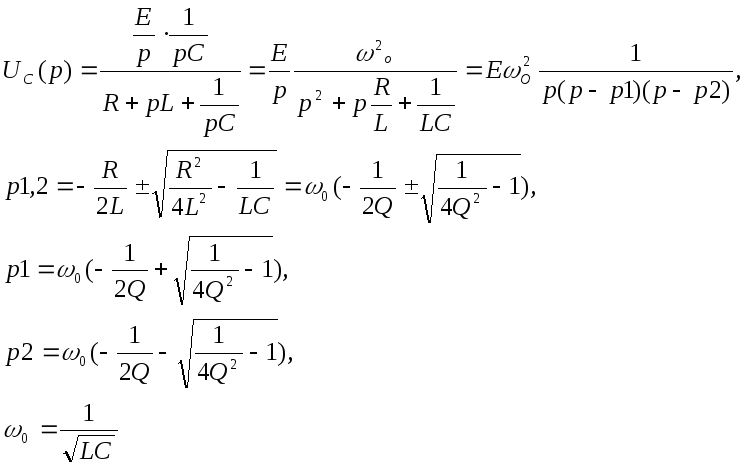(3.16)

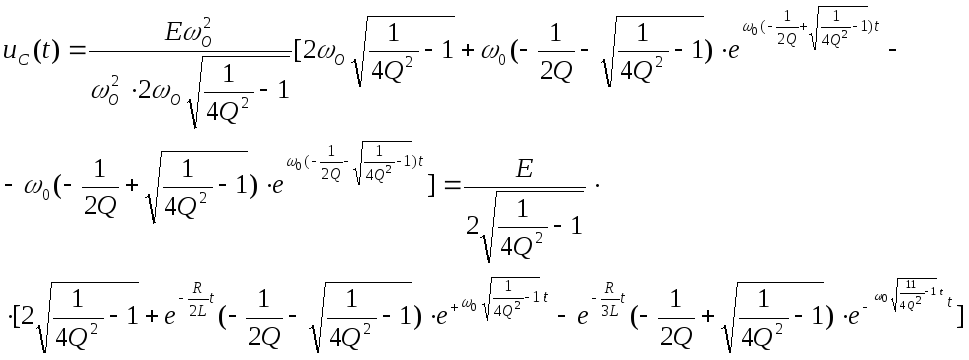(3.17)

Из последней записи в (3.17) легко провести анализ полученного решения.

При t=0 напряжение на емкостном элементе остаётся равным нулю, несмотря на то, что на узлах 1,1' напряжение равно Е.

Если устремить t→∞, то напряжение на емкостном элементе стремиться к Е.

Объяснение этим фактам можно дать, опираясь на законы коммутации в методе эквивалентных схем.

Для момента t=0, эквивалентная схема имеет вид

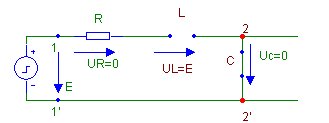
Рис.

Исходя из законов коммутации, емкостной элемент представлен элементом «короткое замыкание», индуктивный – элементом «разрыв».

До момента замыкания ключа К, напряжение на емкостном элементе, как, впрочем, и на других элементах цепи, равно нулю.

Поскольку напряжение на С скачком не может измениться, то и в момент замыкания ключа напряжение на рассматриваемом элементе остаётся равным нулю:

.

Для случая t→∞ цепь представляется другой эквивалентной схемой

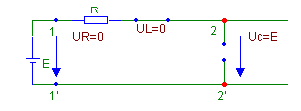
Рис.

В ней показано, что емкостной элемент представлен элементом типа «разрыв», а индуктивный – элементом «короткое замыкание».

Это можно объяснить тем, что при t>0 и t→∞ на входе цепи действует источник постоянного напряжения и, следовательно, токи и напряжения на всех элементах также должны быть постоянными. В этом случае емкостной и индуктивный элементы могут быть заменены рассмотренным.

Напряжение источника находится на емкостном элементе.

Случай корней действительных и равных:

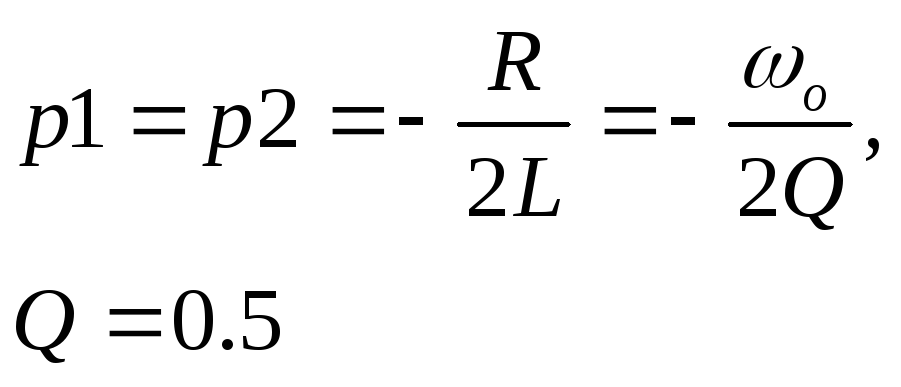
В операторной форме напряжение на емкостном элементе для рассматриваемого случая имеет вид

.

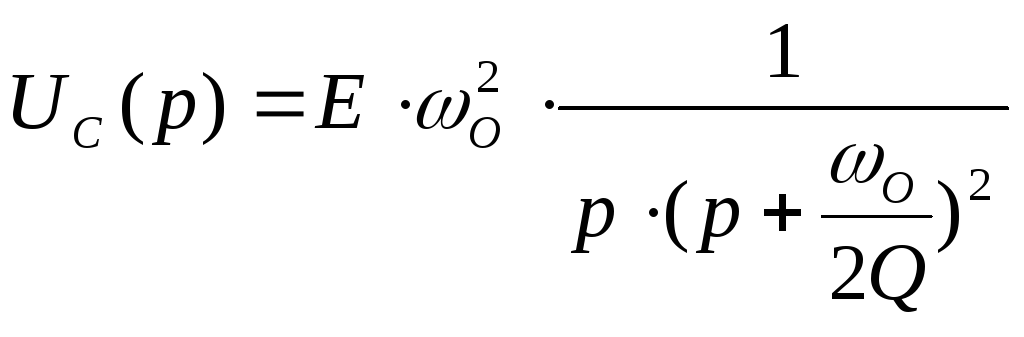Применяя обратное преобразование, получим

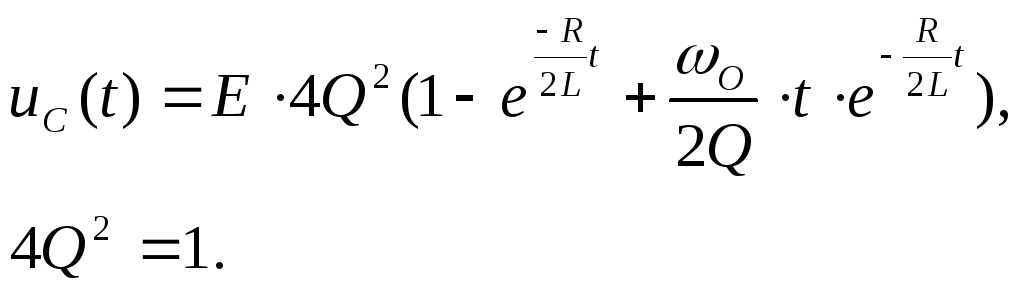(3.18)

Проведём анализ полученного выражения при t≥0.

Пусть t=0. Напряжение на емкостном элементе равно нулю.

При t→∞ напряжение стремится к Е.

Объяснение этому можно дать аналогично сделанному в предыдущем пункте. Различие наблюдается лишь на участке перехода к константе Е.

Случай корней комплексно-сопряжённых:

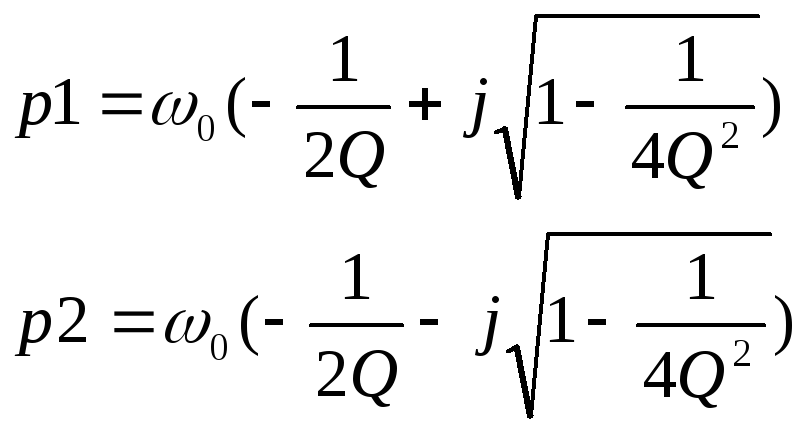
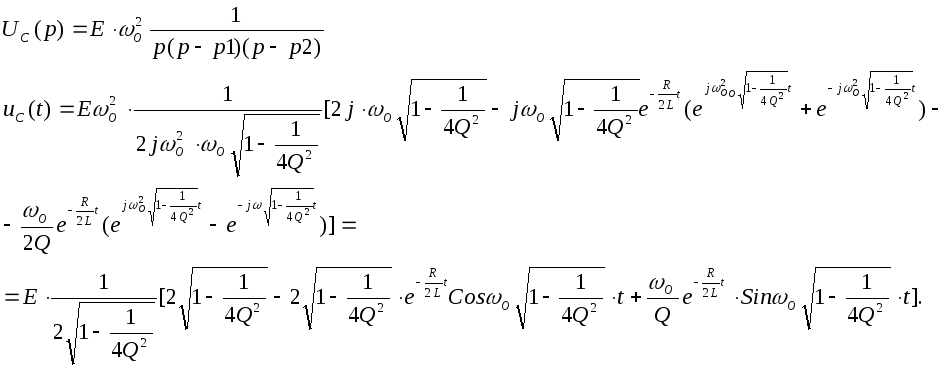
Полученное выражение обозначим (3.19)

Данная формула показывает, что при t=0 напряжение на емкостном элементе равно нулю, а при t →∞ стремится к Е, но этот переход осуществляется в виде затухающего колебательного процесса.

Объяснение этого можно получить аналогично рассмотренному выше.

Проведём нормирование всех напряжений к величине Е- разделим левую и правую части полученных выражений на величину Е.

Получим безразмерное выражение, характеризующее реакцию цепи, если на входе действует единичная функция. Рассматриваемая реакция есть переходная характеристика на узлах 2,2'.

Остаётся за кадром вопрос: на каком основании результаты по законам коммутации, которые получены на схемах закона Ома, могут быть перенесены на поведение этих элементов в сложных схемах?

Какое влияние оказывает сложность схемы?

Скачёк вызывает переходную характеристику и в этом случае схема может быть представлена эквивалентной ?

НОВОЕ К КОЛЕБАТЕЛЬНОМУ КОНТУРУ

(Подход на основе Базиева)

Положим, что ток это есть поток электрино, который представляет собой для схем 2-х-полюсников, замкнутых на источник две волны, бегущие навстречу друг другу и берущие начало на источнике – одна волна у положительного полюса, другая - у отрицательного.

Бегущие навстречу волны создают стоячую волну.

Это явление проявляется для любой электрической схемы, замкнутой на один источник.

Наличие одного источника важный момент, определяющий понятие замкнутости электрической цепи.

Одноконтурная схема, содержащая ветвь источника и ветвь с несколькими пассивными элементами назовём последовательным примитивом.

Любой примитив характеризуется таким явлением как замкнутость.

Пусть положительная волна начинает своё движение от узла1. Она обходит весь путь до узла 1’. Пусть ветвь П однородный проводник. Тогда в такой линии устанавливается удвоенное значение тока – что известно из практики длинных линий. Это означает, что один штопор вошёл в другой и шаг вихря стал в два раза меньше, т.к увеличилась концентрация электрино на единицу длины. Далее волны должны пройти через источник свой –чужой. Чем будет отличаться чужой источник? Он отличается тем, что не создаёт синхронной волны. Один источник создаёт синхронные волны после переходного процесса.

Переходный процесс создаёт синхронизм клемм источника.

Изначально, когда происходит измерение напряжения на источнике, то это напряжение есть следствие разной концентрации числа электрино около полюсов. Это означает, что первоначальные волны разной интенсивности. Навстречу двигаются волны разной интенсивности.

Тренинг с колебательным контуром

На индуктивном элементе напряжение пропорционально производной от тока, значит емкостной ток изменяет(увеличивает или уменьшает) индуктивный ток, в тоже время индуктивный ток также взаимодействует с емкостным током и создаётся заряд, который соответствует резкому увеличению заряда.

Особенность резонанса в том, что напряжения равны и одинаковы по знаку на внешних выводах, потенциал общей точки, если она есть, будет также одинаковый. Возможна схема, когда резистор включён между емкостным и индуктивным элементами. Поскольку напряжения на реактивных элементах должны быть равны, то получается, что резистор на напряжение на каждом не влияет

Для моей теории это определённая концентрация электрино.

Ток в последовательном примитиве одинаков.

При резонансе напряжений, напряжения на индуктивном и емкостном элементах равны. Но один из них определяется интегральным оператором, другой первой производной от тока. Это означает, что цепь, построенная как примитив RLC должна выполнять одновременно функцию интегрирования и дифференцирования, что должно иметь место при каких–то специальных условиях. Из примитивов RL и RC нам известны условия, при которых происходит в этих схемах дифференцирование и интегрирование, но они, в этом случае рассматриваются как 4-х-полюсники. В них интегрирование и дифференцирование

В случае последовательного контура, должно происходить интегрирование и дифференцирование тока в одной ветви, и в случае добротного контура сопротивления на резонансной частоте ёмкости и индуктивности равны и больше резистивного. Это означает, что эти сопротивления определяют ток ветви и ток через резистор уже определён характеристическим сопротивлением.

Поэтому можно поставить вопрос так: Контур добротен, если модули комплексных сопротивлений индуктивного и емкостного элементов существенно превышают резистивное.

Здесь можно сформулировать методический подход – вести весь материал на основе соотношения сопротивлений.

Надо доказать, что мощность выделяемая при резонансе на L или C более мощности, которая выделяется источником.

Повышение добротности это путь к линии без потерь, об этом свидетельствует пример колебательного контура: чем выше добротность, тем отчётливее проявляется главенство реактивного сопротивления и его величина равна волновому сопротивлению линии без потерь.

ОСНОВЫ ТЕОРИИ ФУНКЦИОНАЛЬНЫХ ИНТЕГРАЛЬНЫХ

ПРЕОБРАЗОВАНИЙ

Резистивные элементы характеризуются величиной сопротивления

Структура цепи на основе простейших 4-х-полюсников

Разделы лекции

• Понятие «4-х-полюсник». Токи и напряжения.

• Схемы простейших 4-х-полюсников со всеми токами и напряжениями. Получение формул для напряжения U₂ топологическими методами, т. е. опираясь на геометрические свойства – последовательное или параллельное соединения или на алгебраические- составление уравнений на основе аксиом.

Развитие понятия «передаточная функция». Определение понятия как отношения напряжений в комплексных амплитудах.

.

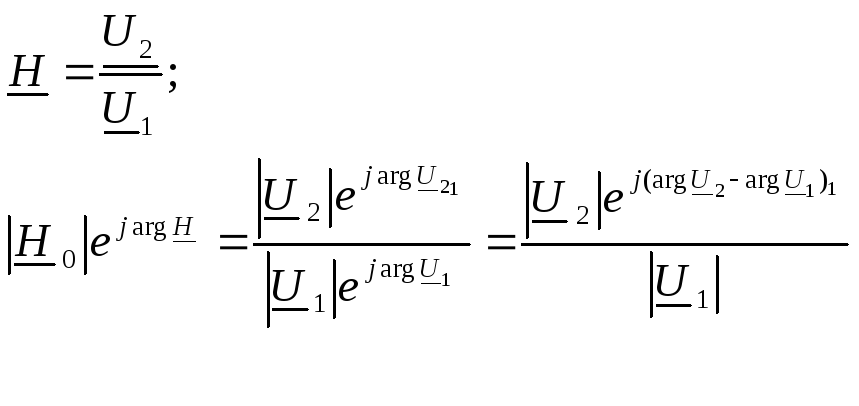Пример. Пусть на входе действует напряжение

u1(t)=U_m1 Sin (ωt + φ).

На выходе 4-х-полюсника напряжение этой же частоты будет

u2(t)=U_m2 Sin (ωt - φ).

Представим эти напряжения в комплексной форме

• Получение понятий «входное сопротивление» и «передаточная функция». Это можно сделать на цепях 1 порядка.

• После изучения А-формы следует рассмотреть вопрос входного сопротивления. Если при этом рассматривать одиночный 4-х-полюсник, то ток I2 =0, следовательно Z_вх=A_1,1/A₂₁. Где А₁₁ есть отношение 1/H₂₂. Тогда для данного 4-х-полюсника можно записать Z_вх*A₂₁*H₂₂=1. Полученная формула позволяет расширить возможности изучения параметров схемы.

• После изучения Z – формы можно сформулировать выражение передаточной функции в общем виде 4-х-полюсника для I2=0 Н22=U₂/U₁=Z₂₁/Z₁₁.

МЕТОД ЭКВИВАЛЕНТНЫХ СХЕМ

Здесь должен быть сформулирован общий подход

- должны быть известны законы коммутации;

- должны быть известны эквивалентные преобразования.

- должны быть известны основные аксиомы.

Можно ли это всё изложить без формул? А почему отсутствие формул считается большим достоинством?

Допустим, законы коммутации можно

Метод эквивалентных схем охватывает временной и частотный подход. Главное в методе акцент на эквивалентные схемы. Там нужно различать момент создания схемы и момент снятия информации со схемы. Это два отдельных методических момента.

Важность метода в том, что это мышление схемное, развитие этого мыслительного аппарата является необходимым в образовательном развитии.

ВХОДНОЕ СОПРОТИВЛЕНИЕ ПОСЛЕДОВАТЕЛЬНОГО КОНТУРА RLC. РЕЗОНАНС НАПРЯЖЕНИЙ.

ВХОДНАЯ ПРОВОДИМОСТЬ ПАРАЛЛЕЛЬНОГО КОНТУРА RLC. РЕЗОНАНС ТОКОВ.

РЕЗОНАНСЫ

ОБРАТНАЯ СВЯЗЬ

Обратная связь возникает как задача управления. Определяется 4-х-полюсник, для которого требуется построить процедуру управления входным напряжением.

Когда речь идёт о напряжении, всегда нужно уточнить форму его представления.

Имея в ввиду гармоническое представление, следует управлять амплитудой и начальной фазой.

Общее название раздела может быть таким:

Управление параметрами входного напряжения одного из соединённых между собой четырёхполюсников, на основе напряжений сформированных во втором.

Четырёхполюсники объединяются в систему. Следствием этого является установление взаимных связей. Наличие этих связей определяет возможность взаимовлияния.

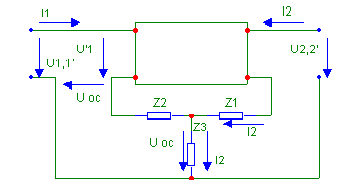
Рис. 1

На рис.1 показано включение цепи обратной связи последовательное по входу и последовательное по выходу. Это обратная связь по току.

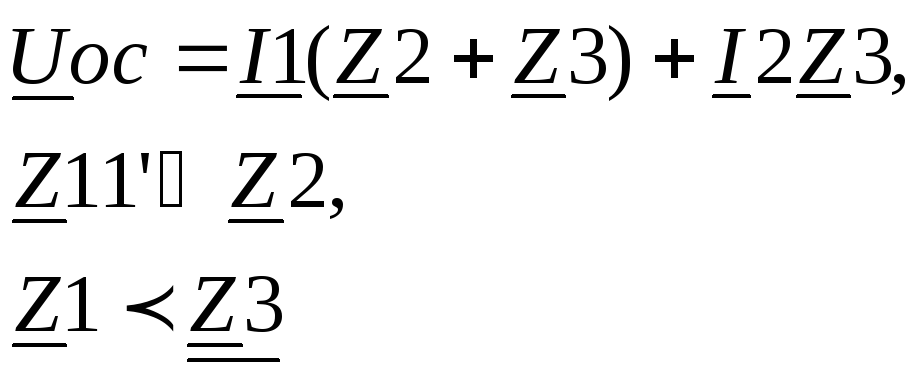(1)

В данном случае набор неравенств определяет условия, при которых напряжение обратной связи определяется в основном током I2.

Рис.2

На рис .2 показано включение обратной связи по напряжению, последовательное по входу и параллельное по выходу.

Сформулируем условия, при которых напряжение обратной связи будет определяться током I2.

(Z2+Z3)<Z'11, Z2>Z1, Z3<Z1.

Получим для данной схемы выражение передаточной функции цепи, охваченной обратной связью.

( )

Рис.3

На рис.3 показана обратная связь по току с параллельным включением по входу. По выходу это есть последовательное включение.

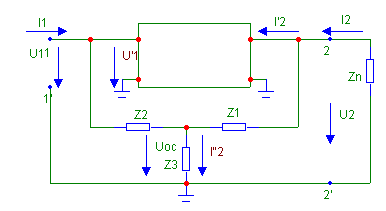
Рис.4

На рис.4 показана обратная связь по напряжению, обеспеченная параллельно, параллельным соединением двух 4-х-полюсников.

В рассмотренных схемах входное сопротивление первого четырёхполюсника есть элемент, на котором происходит суммирование напряжений.

При параллельном по входу соединении модуль Z2 выбирается много больше модуля входного сопротивления Z'₁₁.

ФУНКЦИЯ ИСТЧНИКА – ФУНКЦИЯ НА ОГРАНИЧЕННОМ МНЖЕСТВЕ ОПРЕДЕЛЕНИЯ (ОДИНОЧНАЯ ФУНКЦИЯ ИСТОЧНИКА НАПРЯЖЕНИЯ)

Данное определение характеризует условие работы источника энергии.

Суть дела в том, что одиночность функции следует понимать как состояние функционирования цепи, в котором простой (нефункциорирование) цепи прерывается редкими промежуткам реакции цепи, причём время реакции много меньше времени простоя.

Однако этому представлению можно придать более точный вид:

- время реакции цепи меньше минимального времени последовательности.

РЕАКЦИЯ цепи.

Это вопрос требует специального подхода.

Различают два класса реакций. Для их определения необходима мера изменчивости реакции определяемая собственными свойствами цепи. Изменение, например, увеличение напряжения источника пусть вызывает увеличение на выходе, точнее, вызывает изменение той функции, по которой определяется реакция.

СЛЕДОВАТЕЛЬНО, для определения следует указать, что следует понимать под реакцией. Чаще всего такой величиной будет выступать напряжение между какими-нибудь узлами, т. е. u_m,n(t).

Для определения числовых характеристик требуется задание стандартного, одинакового входного напряжения, которое определено на числовом множестве. Одним из таких является формализованная функция включения, которая берётся из схемы для изучения закона Ома с постоянным источником.

ДИСКРЕТНЫЕ ЦЕПИ

Представим процесс дискретизации непрерывной функции времени.

u*_1,1'(t) = u_1,1'(t)p(t),

где p(t) =1, 0< t < t_и,

0 , t_и < t < T.

u_1,1'(t) – есть множество точек на графике, а p(t) - тоже множество точек. Их произведение, рассматриваемое как элемент нового множества, тоже есть точка.

Далее, представим технически реализацию подобной операции в виде схемы с ключом, который коммутирует цепь для прохождения тока через конденсатор на интервале t_и.

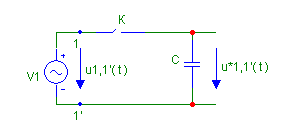
Рис.1

С учётом внутреннего сопротивления источника, данная цепь производит интегрирование тока и формируется напряжение пропорциональное входному, на интервале времени включённого состояния ключа К, который замкнут, т.е. происходит взаимодействие, на интервале t_и.

Результат дискретизации представляет импульс, т.е. не точка графика, а импульс, площадь, интеграл. Но описать, с точки зрения мгновенного значения, можно, проведя аналогично p(t), т.е. указать интервал изменения t, в котором можно указать значение высоты импульса, одинаковое для всех точек интервала. Это значение принимается за мгновенное значение. Чтобы это действительно было бы для всех точек интервала, нужно чтобы постоянная времени цепи, в которой происходит процесс дискретизации, была бы равна нулю.

Результат работы цепи – импульс, интеграл. Размерность результата В*с. Это размерность преобразования Лапласа.

Получение дискретной функции источника на основе дельта-дискретизации.

В основе определения лежит интеграл

,

в котором u_1,1' (t) – непрерывная функция времени, δ(t)- дельта-функция, выступающая как импульсная характеристика, m – целое число точек, на которых задаётся процесс дискретизации. Интеграл не может быть равным сумме. Эта запись имеет право на существование как отражение процесса дискретизации.

Собственно, процедура превращения непрерывной функции в дискретную по времени заключена не в математической сущности интегрирования на основе δ(t)- функции, поскольку каждый раз рассматривается одна точка с бесконечно малой окрестностью, а на основе принятия сущности соответствующей дискретному множеству точек для выборки.

Как следует из определения этой функции, процесс интегрирования заключается в применении теоремы о среднем на бесконечно малой области, которой принадлежит точка, в которой δ(t) = ∞.

Таким образом, проводится дискретизация оси времени t точками, в которых задаётся δ(t). Расстояние между этими точками принимается равным некоторому интервалу Т.

Для каждой точки «m» интегрирование определяется формулой

.

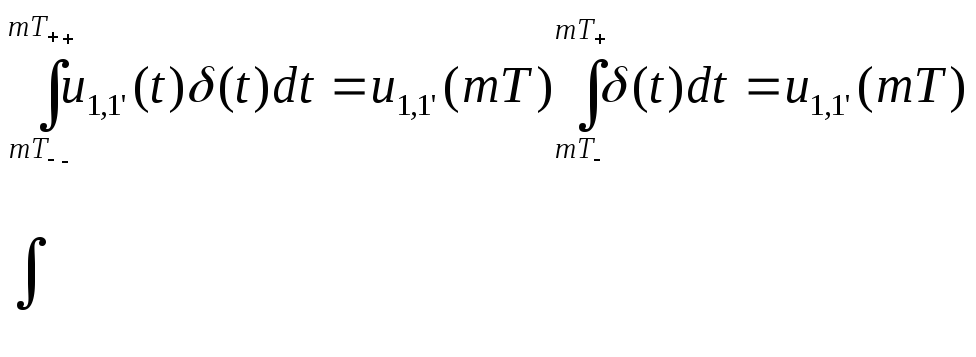Совокупность таких значений можно записать в виде суммы по количеству точек, как это сделано в исходной формуле.

В литературе принято всю представленную процедуру заменить операторным представлением

u_1,1'(t)δ(t) = U_1,1',

где U_1,1' – мгновенное значение функции u_1,1'(t) в момент времени t, δ(t) – интерпретирована единичным импульсом.

Формула показывает результат: запись

u_1,1'(t)δ(t)

означает мгновенное значение U_1,1', соответствующее моменту времени t.

Полученное выражение дискретной функции времени можно использовать для получения соответствующего преобразования Лапласа от δ(t) - дискретизированной функции времени.

Следует здесь отметить, что преобразование Лапласа от последовательности прямоугольных импульсов разной амплитуды расходится и лишь δ(t) - последовательность даёт возможность получить указанное преобразование.

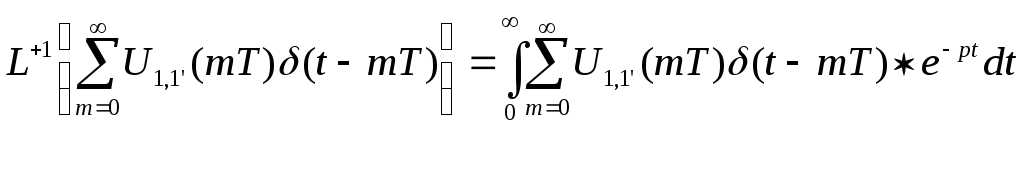
Если провести преобразование – внести интеграл под знак суммы и провести интегрирование в области точки «m» с учётом δ(t) функции, можно получить выражение

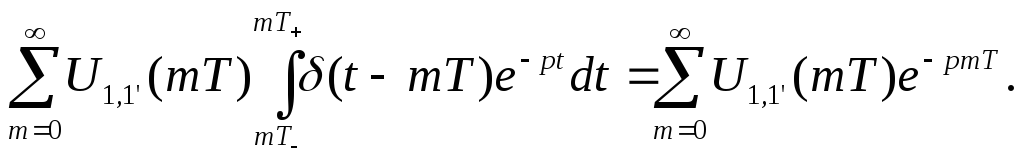
Если ряд сходится, то полученная формула представляет непрерывную функцию от комплексной частоты «p».

Положим z = e^pT.

Тогда полученное выражение перепишем с обозначением результата в виде функции от z.

Это выражение, при условии, что ряд сходится, носит название Z - преобразования из временной области в частотную (область комплексных частот). Особенность этого вида преобразования по отношению к известным – Фурье и Лапласу – заключается в том, что это частотное преобразование дискретной во временной области функции. Однако, если рассматривать зависимость модуля и аргумента функции U_1,1'(z) от частоты, то они представляют собой непрерывные функции по частоте.

Рассмотрим несколько примеров.

Пусть рассматривается аналог единичной функции в дискретной области

1(mT). Z – преобразование запишется в виде

Сумму можно представить в виде

Если |z|>1, то данный ряд сходится, и сумма ряда определяется по формуле

.

Проверим, выполняется ли принятое предположение для z = e^pT, если принять p = jω.

В этом случае z = CosωТ + jSinωТ и модуль z равен 1. Предположение не выполняется, однако если принять в качестве p полное выражение комплексной частоты p = σ + jω, то принятое предположение относительно модуля z будет выполняться.

В дальнейшем будем полагать под z именно такое условие.

Таким образом, преобразование

от дискретной единичной функции времени есть дробно – рациональное выражение в z области.

Рассмотрим другую, скажем, экспоненциальную функцию.

Пусть дискретная функция задана формулой

♥ u_1,1'(mT) =exp(αmT), t>0.

Соответствующее Z-преобразование имеет вид

♪ U_1,1'(z) = .

В этом выражении отношение, заданное в скобках также можно рассматривать как геометрическую прогрессию. Следовательно, если |exp(αT)/z|<1, то ряд сходится и сумма имеет вид

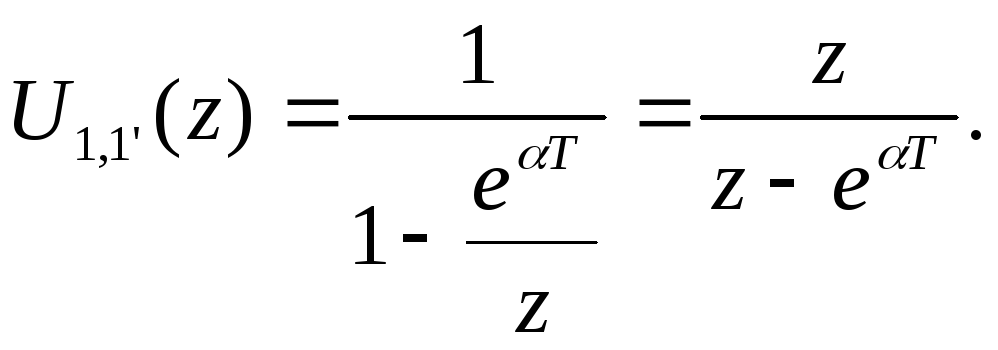
Рассмотрим линейную функцию

U_1,1'(z) = .

Приём, который здесь применён, может быть использован и в других случаях, например для степенных функций от t^к:

.

Здесь возможно представление примера, в котором можно построить графики некоторой дискретной по временной оси функции и её представление в Z- форме, также используя по временной оси дискретное множество точек. Это распределение целых чисел, начиная с нуля. На каждой точке восстановим столбик высотой соответствующей амплитуды у Z в степени равной (-к).

Разностное уравнение и его характеристическое уравнение

На множестве значений дискретизированной по аргументу функции можно ввести известные операции сложения (вычитания), умножения (деления) и, в дополнение к ним, оператор смещения:

,

который по смыслу определяет выборку значения функции сдвинутой относительно исходного значения на «к» единиц влево (со знаком минус) или вправо.

Построим выражение, представляющее аналог первой производной (правой) для непрерывной по аргументу функции:

Получим выражение для второй производной:

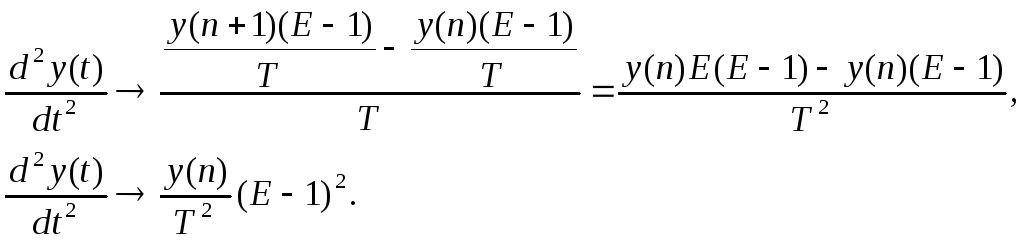
Обозначим разность в скобках между оператором сдвига и единицей через Δ и назовём РАЗНОСТНЫМ оператором.

В этих обозначениях дискретные аналоги производных можем записать:

y(n)Δ/Т,

Полученные выражения для «производных» позволяют поставить вопрос о возможности написания уравнений в разностных представлениях, которые, в определённом смысле, подобны дифференциальным.

Как возникает разностное уравнение?

А как возникает дифференциальное уравнение?

Рассмотрим пример. Пусть имеется простейшая цепь, состоящая из тёх элементов, которые последовательны : источника напряжения, резистора и емкостного элемента.

По второму закону напишем

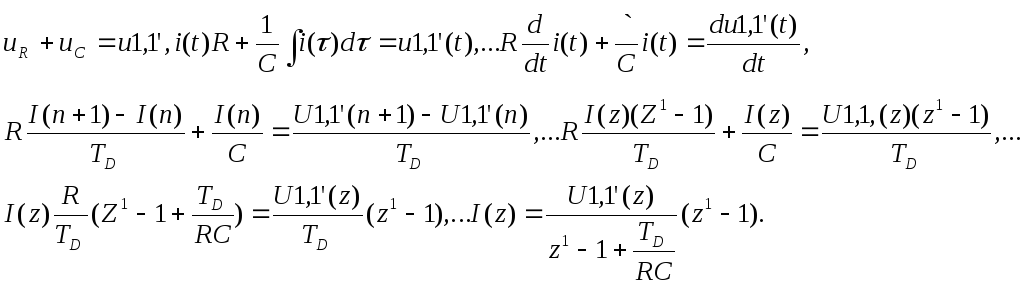
Последняя формула определяет величину тока в рассматриваемой цепи поскольку z непрерывная величина по комплексной частоте, то можно говорить о частотной характеристике в области дискретных частот.

Подобный подход позволяет начинать излагать теорию цепей с дискретных цепей.

Запись требует определение 2-х-полюсников в дискретной области через конечные приращения.

Начнём с экспериментальных данных по схемам.

Все кривые тока и напряжения представляем дискретным набором и пытаемся полученным графикам поставить в соответствие математическую операцию (оператор), связывающую функции тока и напряжения, которые заданы на одном и том же множестве значений времени.

Скачкообразное изменение в бесконечной малой области можно представить оператором смещения

Разовьём соображения относительно получения формулы, которая связывает параметры элементов в ПК-эквивалентах.

Вывод формул проведём для трёх ПК-эквивалентов.

Условием эквивалентности будем считать равенство зарядов, которые протекают через резистор и емкостной элемент за некоторый интервал времени Т в схеме с двумя источниками. Функции источников представляют дискретные по времени, которые можно представить как некоторые функции тока на интервале Т.

Рассмотрим ПРОЦЕСС получения дискретизированного напряжения во временной области и рассмотрим влияние процесса на характер его спектра (область мнимых частот).

Процесс получения во временной области можно представить произведением 2-х функций времени (см. схему с ключом)

u_1,1'(t)^* = u_1,1'(t) р(t),

в которой р(t) можно представить как последовательность прямоугольных импульсов, длительность которых много меньше периода следования Т. В пределе эту последовательность можно представить последовательностью δ(t) – импульсов.

Если K(t) периодическая последовательность, то её можно записать рядом Фурье

.

Подставляя эту запись в предыдущую формулу, ПОЛУЧИМ

.

Применим к обеим частям равенства интеграл Фурье и получим спектральную функцию дискретизированного напряжения:

.

Спектральная функция входного напряжения в рассматриваемом случае есть периодическая функция с периодом равным частоте первой гармоники для периодической последовательности K(t), т.е. 1/Т либо 2π/Т.