Метод парабол (метод Симпсона)

Использовав три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид

.

Если разбить интервал интегрирования на равных частей, то имеем

где .

Листинг программы в приложении

Результат работы программы

Для двух отрезков

vvedite znachenija koncov otrezka [a,b]

0 1.57

Vvedite chislo razbieniy otrezka n

2

s1= 0.638921 s2= 0.436401 s3= 0.571414

Dlja prodolgenija nagmite lubuyu klavishu

Погрешность 0,000414

Для 4-ех отрезков

vvedite znachenija koncov otrezka [a,b]

0 1.57

Vvedite chislo razbieniy otrezka n

4

s1= 0.587420 s2= 0.537661 s3= 0.570834

Dlja prodolgenija nagmite lubuyu klavishu

Погрешность 0,000164

2. Вычислить интеграл, используя квадратурную формулу Гаусса с тремя узлами для числа разбиения отрезка интегрирования n=1. Оценить погрешность результата. Сравнить приближенные значения интеграла со значениями, полученными в упражнении 1 и с точными значениями.

3.1. Квадратурная формула Гаусса

Пусть функция задана на стандартном интервале . Задача состоит в том, чтобы подобрать точкии коэффициентытак, чтобы квадратурная формула

(3.1)

была точной для всех полиномов наивысшей возможной степени.

Ввиду того, что имеется параметрови, а полином степениопределяетсякоэффициентами, эта наивысшая степень в общем случае.

Запишем полином в виде и подставим в (3.1). Получим

,

.

Приравнивая выражения при одинаковых коэффициентах получим

, ,

, .

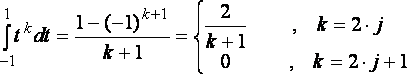Итак, инаходят из системыуравнений

,

,

, (3.2)

. . . . . . .

.

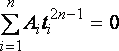Система (3.2) нелинейная, и ее решение найти довольно трудно. Рассмотрим еще один прием нахожденияи. Свойства полиномов Лежандра

,

таковы:

1) ,;

2) ;

3) полином Лежандра имеетразличных и действительных корней, расположенных на интервале.

Составим по узлам интегрирования многочлен -й степени

.

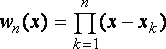Функция приесть многочлен степени не выше. Значит для этой функции формула Гаусса справедлива:

, (3.3)

так как .

Разложим в ряд по ортогональным многочленам Лежандра:

,

,

,

т.е. все коэффициенты при. Значитс точностью до численного множителя совпадает с. Таким образом, узлами формулы Гаусса являются нули многочлена Лежандра степени.

Зная , из линейной теперь системы первых(3.2) легко найти коэффициенты. Определитель этой системы есть определитель Вандермонда.

Формулу , в которой- нули полинома Лежандра, аопределяют из (3.3), называют квадратурной формулой Гаусса.

Пример. Вывести квадратурную формулу Гаусса для случая трех ординат .

Полином Лежандра третьей степени

.

Корни:

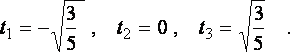
Из (3.2) имеем

,

,

.

Отсюда

.

Тогда

.

Рассмотрим теперь применение квадратурной формулы Гаусса для вычисления интеграла с не единичными пределами :

.

Получим

,

,

где

, ;

- нули полинома Лежандра , т.е..

Остаточный член формулы Гаусса с узлами выражается формулой

.

Отсюда следует

,

,

и т.д.

Листинг в приложении

Результат работы программы

vvedite znachenija koncov otrezka [a,b]

0 1.57

Vvedite tochnost` vichisleniya epsilon

0.000001

Velichina integrala s= 1.570797 Pogreshnost` d= 0.000001

Dlja prodolgenija nagmite lubuyu klavishu

Погрешность от точного значения 0,000203,

От значения по методу Симпсона 0,000037

Задание 5

Найти решение задачи Коши для дифференциального уравнения перво­го порядка на равномерной сетке отрезка [а,b ] один раз с ша­гом h=0,2, другой - с шагом 0,1 методами Эйлера, Эйлера - Ко­ши и классическим методом Рунге - Кутта. Оценить погрешность численного решения по принципу Рунге. Сравнить численное ре­шение с точным. Результаты представить в виде таблиц, анало­гичных приведенным в примерах этого параграфа.