1.2. Уточнение корней методом половинного деления (дихотомии)

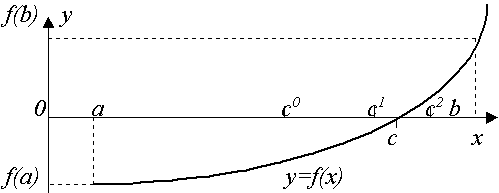
Рис. 1. Метод деления отрезка пополам

Самым простейшим из методов уточнения корней является метод половинного деления, или метод дихотомии, предназначенный для нахождения корней уравнений, представленных в виде f(x)=0.

Пусть непрерывная функция f(x)на концах отрезка [a,b] имеет значения разных знаков, т.е.f(a)* f(b) <= 0(рис. 1), тогда на отрезке имеется хотя бы один корень.

Возьмем середину отрезка с=(a+b)/2. Еслиf(a)* f(b) <= 0, то корень явно принадлежит отрезку отaдо(a+b)/2и в противном случае от(a+b)/2доb.

 

 

 

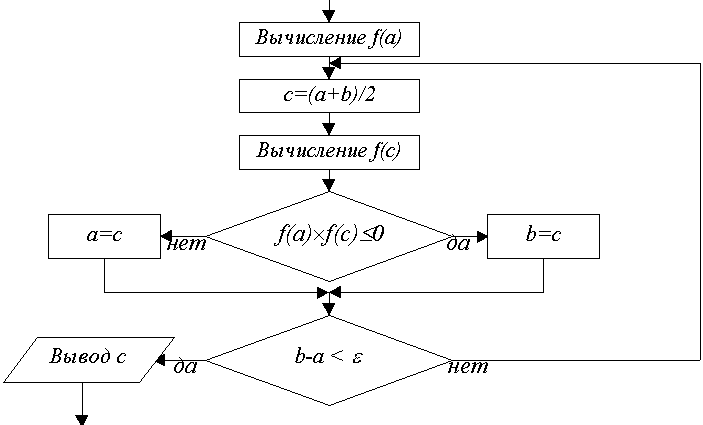Рис. 2. Блок-схема метода половинного деления

Поэтому берем подходящий из этих отрезков, вычисляем значение функции в его середине и т.д. до тех пор, пока длина очередного отрезка не окажется меньше заданной предельной абсолютной погрешности (b-a)<e.

Так как каждое очередное вычисление середины отрезка cи значения функцииf(c)сужает интервал поиска вдвое, то при исходном отрезке [a,b] и предельной погрешностиe количество вычисленийnопределяется условием(b-a)/2ⁿ<e , илиn~log₂((b-a)/e ). Например, при исходном единичном интервале и точности порядка6знаков (e ~ 10^-6) после десятичной точки достаточно провести20вычислений (итераций) значений функции.

С точки зрения машинной реализации (рис. 2) этот метод наиболее прост и используется во многих стандартных программных средствах, хотя существуют и другие более эффективные по затратам времени методы.

Листинг программы в приложении

Результат работы программы

Vvedite po porjadku 3 chisla

koordinaty koncov otrezka a,b, tochost epsilon

-1 1 0.01

2

x= 0.0000000000E+00

Pogreshnost rezultat = 1.0000000000E+00

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.0000000000E-01

Pogreshnost rezultat = 5.0000000000E-01

Dlja prodolgenija nagmite lubuyu klavishu

x=-7.5000000000E-01

Pogreshnost rezultat = 2.5000000000E-01

Dlja prodolgenija nagmite lubuyu klavishu

x=-6.2500000000E-01

Pogreshnost rezultat = 1.2500000000E-01

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.6250000000E-01

Pogreshnost rezultat = 6.2500000000E-02

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.9375000000E-01

Pogreshnost rezultat = 3.1250000000E-02

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.7812500000E-01

Pogreshnost rezultat = 1.5625000000E-02

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.7031250000E-01

Pogreshnost rezultat = 7.8125000000E-03

Dlja prodolgenija nagmite lubuyu klavishu

2 Метод итераций

1.5. Уточнение корней методом простой итерации

Другим представителем итерационных методов является метод простой итерации.

Здесь уравнение f(x)=0заменяется равносильным уравнениемx=j (x)и строится последовательность значений

.

Если функция j (x)определена и дифференцируема на некотором интервале, причем|j /(x)|< 1, то эта последовательность сходится к корню уравненияx=j (x)на этом интервале.

Геометрическая интерпретация процесса представлена на рис. 7. Здесь первые два рисунка (а, б) демонстрируют одностороннее и двустороннее приближение к корню, третий же (в) выступает иллюстрацией расходящегося процесса (|j /(x)| > 1).

а	б	в
Рис. 7. Геометрическая интерпретация метода простой итерации

Если f '(x)>0, то подбор равносильного уравнения можно свести к заменеx=x-l Ч f(x), т.е. к выборуj (x)= x-l Ч f(x), гдеl >0подбирается так, чтобы в окрестности корня 0 < j '(x)=1- l Ч f '(x) Ј 1. Отсюда может быть построен итерационный процесс

.

где M і max |f '(x)| (в случае f '(x)< 0 возьмите функцию f(x) с противоположным знаком).

Возьмем для примера уравнение x³ + x -1000 = 0. Очевидно, что корень данного уравнения несколько меньше10. Если переписать это уравнение в видеx =1000 - x³и начать итерационный процесс приx₀=10, то из первых же приближений очевидна его расходимость. Если же учестьf '(x)=3x²+1>0и принять за приближенное значение максимумаf '(x) M=300, то можно построить сходящийся итерационный процесс на основе представления

.

Можно и искусственно подобрать подходящую форму уравнения, например:

или .

Заметим, что существуют и другие методы (наискорейшего спуска, Эйткена-Стеффенсена, Вегстейна, Рыбакова и т.д.) уточнения корней, обладающие высокой скоростью сходимости.

Преобразуем функцию в вид x=g(x). Получим

x= -e^x

	x		G(x)	Y=x
-5		-0,006738			-5
-4		-0,018316			-4
-3		-0,049787			-3
-2		-0,135335			-2
-1		-0,367879			-1
0		-1,000000			0
1		-2,718282			1
2		-7,389056			2
3		-20,085537			3
4		-54,598150			4
5		-148,413159			5

Листинг программы в приложении

Результат работы программы

Vvedite po porjadku 2 chisla

Nachalnoe znachenie i tochost epsilon/10

-1 0.01

x=-3.6787944117E-01

Pogreshnost pribligenija d= 6.3212055883E-01

Dlja prodolgenija nagmite lubuyu klavishu

x=-6.9220062755E-01

Pogreshnost pribligenija d= 3.2432118638E-01

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.0047350056E-01

Pogreshnost pribligenija d= 1.9172712699E-01

Dlja prodolgenija nagmite lubuyu klavishu

x=-6.0624353508E-01

Pogreshnost pribligenija d= 1.0577003452E-01

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.4539578598E-01

Pogreshnost pribligenija d= 6.0847749108E-02

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.7961233550E-01

Pogreshnost pribligenija d= 3.4216549526E-02

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.6011546136E-01

Pogreshnost pribligenija d= 1.9496874140E-02

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.7114311508E-01

Pogreshnost pribligenija d= 1.1027653717E-02

Dlja prodolgenija nagmite lubuyu klavishu

x=-5.6487934739E-01

Pogreshnost pribligenija d= 6.2637676874E-03

Dlja prodolgenija nagmite lubuyu klavishu

Результаты, найденные двумя способами, отличаются на 0,055.

Задание 3

1. Нанести экспериментальные точки (xi, yi) на координатную сетку (x,y).

2. Выбрать одну из шести формул преобразования в переменным (X,Y) так, чтобы преобразованные экспериментальные данные (Xi,Yi) наименее уклонялись от прямой.

3. Методом наименьших квадратов найти наилучшие значения параметров k и b в уравнении прямой.

4. Найти явный вид эмпирической формулы y=Q(x,a,b) и построить график эмпирической функции.