05-02

!Taskfile kontr_СМ 2-05-02#Осевые моменты инерции. Зависимость между моментами инерции при параллельном переносе осей

!De=kontr_СМ 2-05#Геометрические характеристики поперечных сечений стержня

!Task1

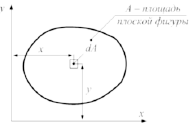
Интегралы 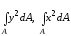называются …

!Solution

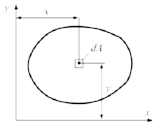
Рассмотрим некоторую плоскую фигуру (см. рисунок). Отнесем ее к системе координат 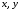. Разобьем площадь фигуры на элементарные площади прямоугольной координатной сеткой. Если каждую элементарную площадь помножить на квадрат координаты y ее центра тяжести и сложить все произведения, то получим осевой момент инерции площади относительно оси x. Чем меньше шаг сетки, тем точнее результат. Заменяя суммирование интегрированием по площади, получаем

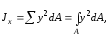
где А – площадь фигуры.

Аналогично определяем осевой момент инерции площади относительно оси y.

!

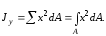
!Task2

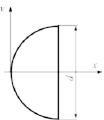
Осевой момент инерции площади полукруга относительно оси x равен …

!Solution

Для круга . Для полукруга .

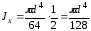!True

!

!Task3

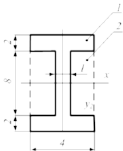
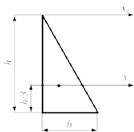
На рисунке размеры поперечного сечения стержня заданы в сантиметрах. Осевой момент инерции площади сечения относительно центральной оси x равен ___ см⁴.

!Solution

Дополним поперечное сечение до прямоугольника, который обозначим цифрой 1. Прямоугольнику с отрицательной площадью присвоим цифру 2. Ось является центральной для прямоугольников 1 и 2.

Осевой момент инерции прямоугольного сечения относительно центральной оси, параллельной основанию, определяется по формуле 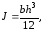где b –ширина прямоугольника; h – высота.

Поэтому при определении осевого момента инерции сечения необходимо из момента инерции прямоугольника 1 вычесть два момента инерции прямоугольника 2, то есть

.

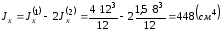!True

448

!Task4

Если 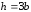, то значение осевого момента инерции площади относительно оси , параллельной основанию, равно …

!Solution

Для вычисления 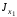используем формулу перехода от центральной оси x к любой, параллельной ей. .

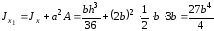!True

!Task5

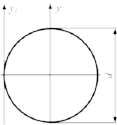
Осевой момент инерции круга относительно оси 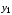равен …

!Solution

Для круглого сечения диаметром 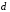осевой момент инерции относительно центральной оси y определяется по формуле .

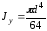Ось 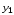расположена параллельно центральной. Используем формулу перехода от центральной оси к любой параллельной ей.

,

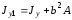где – расстояние между осями 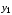и y; А – площадь круга.

Тогда .

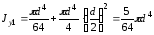!True

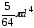
!Task7

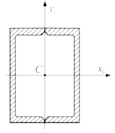
Для сечения, состоящего из двух швеллеров №20, момент инерции относительно оси 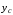равен ___ см⁴.

!Solution

Используя формулу, связывающую моменты инерции относительно параллельных осей, запишем

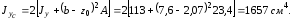
Значение для швеллера №20 взяты из таблицы ГОСТов.

!True

1657

!Task9

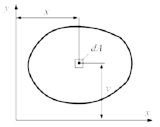
Момент инерции площади – величина …

!Solution

Момент инерции площади фигуры относительно оси x есть интеграл вида 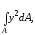где А – площадь фигуры. Координата у входит под знак интеграла в квадрате. Площадь – величина всегда положительная. Поэтому момент инерции относительно любой оси – величина всегда положительная.

!