2. Второй постулат Бора (правило частот).

При переходе электрона с одной стационарной орбиты на другую излучается или поглощается фотон с энергией

h_km=E_k-E_m

равной разности энергий соответствующих стационарных состояний до и после излучения или поглощения. При E_k > E_m происходит излучение фотона, т.е. переход атома на близлежащую к ядру орбиту, при E_k < E_m поглощение, т.е. переход на более удаленную орбиту

.

3. Постулат квантования момента импульса.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию

( n=1,2,… ) ,

где m_e-масса электрона; v_n-его скорость по n-й орбите радиуса r_n; h=6,63·10^-34 Дж·с- постоянная Планка.

1.2 Модель водородоподобного атома по Бору

В предположении, что электрон движется в водородоподобном атоме по круговой орбите, постулаты Бора позволяют найти:

1) радиусы r_n стационарных орбит электрона:

2) энергетические уровни E_n электрона в атоме

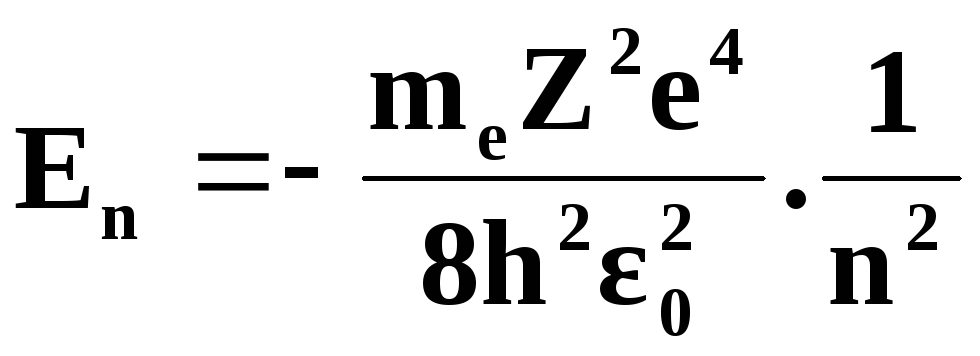
3) частоту света, испускаемого (поглощаемого) при переходе k  m

,

здесь R=3,2921·10¹⁵ с^-1- постоянная Ридберга, k=m+1,m+2, …

4) длину волны излучения, связанного с переходом km

1.3 Корпускулярно-волновой дуализм

Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики - энергия E и импульс p , а с другой - волновые характеристики – частота  и длина волны λ. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотона:

В классической механике (v « c) импульс определен формулой , гдеm- масса частицы.

Для релятивистских условий, когда скорость движения соизмерима со скоростью света в вакууме:

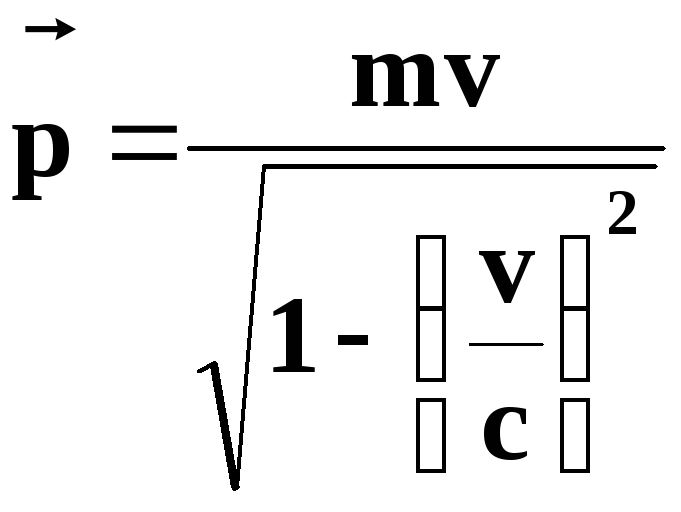
Выражая импульс через кинетическую энергию E_k, получаем

для классической механики:

для релятивистских условий:

, где Е₀ – энергия покоя.

1.4 Соотношение неопределенностей

В силу двойственной корпускулярно-волновой природы частиц вещества существуют ограничения в применении к микрообъектам понятий классической механики, в частности, понятия траектории. Дело в том, что понятие «длина волны в данной точке» лишено физического смысла- это понятие интегральное. С другой стороны, длина волны однозначно связана с импульсом. Таким образом, если микрочастица имеет определенный импульс, она имеет определенную длину волны и, следовательно, полностью неопределенную координату.

В общем виде эта связь выражается принципом неопределенности Гейзенберга: а) для координат и импульса:

где Δp_i- неопределенность проекции импульса на ось i ; Δx, Δy , Δz -неопределенности координат.

Б) для энергии и времени:

где ΔE и Δt - неопределенности энергии и времени, в течение которого измеряется энергия.

Соотношение неопределенностей не ставит предел в познании микромира. Оно является квантовым ограничением применимости классической механики к микрообъектам.

1.5 Одномерное стационарное уравнение Шредингера

Более последовательной теорией описания микрочастиц в различных силовых полях является квантовая механика. Основным уравнением этой теорией является уравнение Шредингера относительно волновой функции микрочастицы, например электрона в водородоподобном атоме.

В простейшем случае одномерного движения для стационарных силовых полей U=U(x) уравнение Шредингера принимает вид:

где E и U – полная и потенциальная энергия частицы; Ψ(x) – координатная часть волновой функции.

Физический смысл волновой функции раскрывается через вероятность обнаружения частицы в интервале координат (x,x+dx):

dw=│Ψ(x) │²dx , где │Ψ(x) │²- плотность вероятности.

Вероятность обнаружить частицу в конечном интервале координат (например, в одномерной потенциальной яме) от x₁ до x₂:

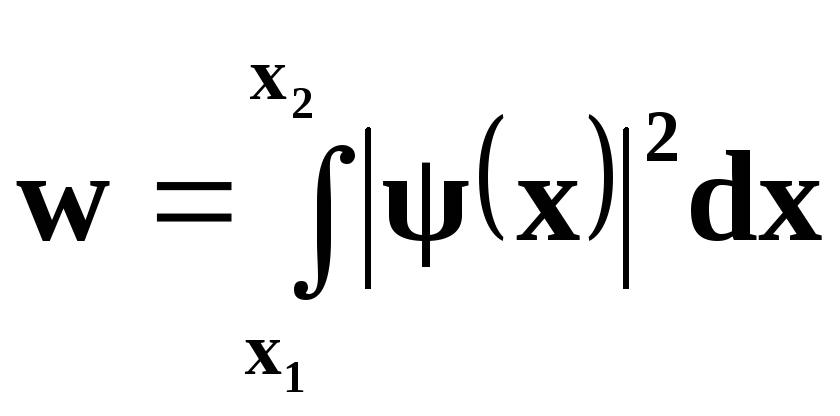
Пусть L - ширина потенциальной ямы при бесконечных значениях потенциальной энергии на краях ямы. Тогда собственные значения энергии частицы на энергетическом уровне с квантовым числом n определяются формулой: