Lektsia_8

Введение.

На лекции изучаются ЛНДУ – линейные неоднородные дифференциальные уравнения. Рассматривается структура общего решения, решение ЛНДУ методом вариации произвольных постоянных, решение ЛНДУ с постоянными коэффициентами и правой частью специального вида. Рассматриваемые вопросы применяются при изучении вынужденных колебаний в физике, электротехнике и электронике, теории автоматического управления.

1. Структура общего решения линейного неоднородного дифференциального уравнения 2 порядка.

Рассмотрим сначала линейное неоднородное уравнение произвольного порядка:

С учетом обозначения можно записать:

При этом будем полагать, что коэффициенты и правая часть этого уравнения непрерывны на некотором интервале.

Теорема. Общее решение линейного неоднородного дифференциального уравнения в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения.

Доказательство. Пусть Y – некоторое решение неоднородного уравнения.

Тогда при подстановке этого решения в исходное уравнение получаем тождество:

Пусть - фундаментальная система решений линейного однородного уравнения . Тогда общее решение однородного уравнения можно записать в виде:

Далее, сумма является общим решением неоднородного уравнения.

В частности, для линейного неоднородного дифференциального уравнения 2 порядка структура общего решения имеет вид:

где - фундаментальная система решений соответствующего однородного уравнения, а - какое-либо частное решение неоднородного уравнения.

Таким образом, для решения линейного неоднородного дифференциального уравнения необходимо найти общее решение соответствующего однородного уравнения и каким- то образом отыскать одно частное решение неоднородного уравнения. Обычно оно находится подбором. Способы подбора частного решения рассмотрим в следующих вопросах.

2. Метод вариации

На практике удобно применять метод вариации произвольных постоянных.

Для этого сначала находят общее решение соответствующего однородного уравнения в виде:

Затем, полагая коэффициенты C_i функциями от х, ищется решение неоднородного уравнения:

Можно доказать, что для нахождения функций C_i(x) надо решить систему уравнений:

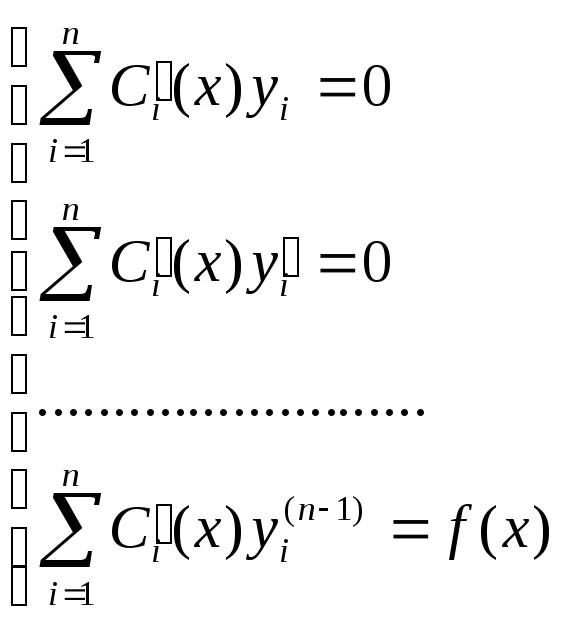
Пример. Решить уравнение

Решаем линейное однородное уравнение

Решение неоднородного уравнения будет иметь вид:

Составляем систему уравнений:

Решим эту систему:

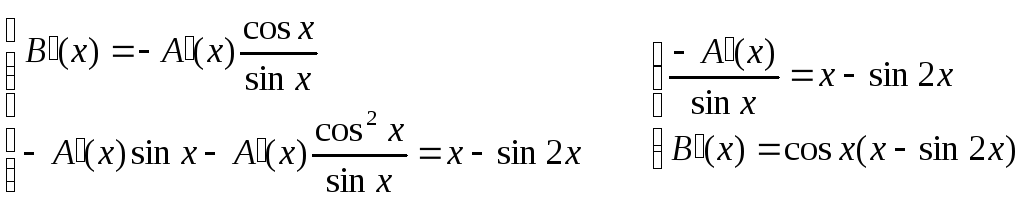
Из соотношения найдем функцию А(х).

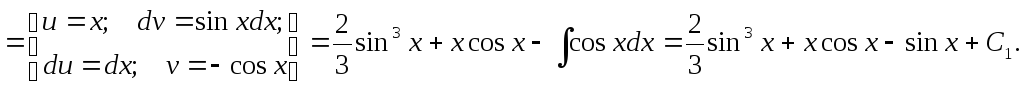
Теперь находим В(х).

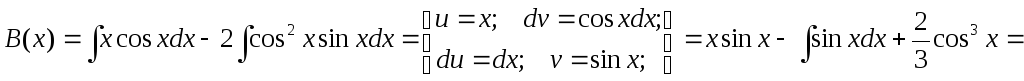
Подставляем полученные значения в формулу общего решения неоднородного уравнения:

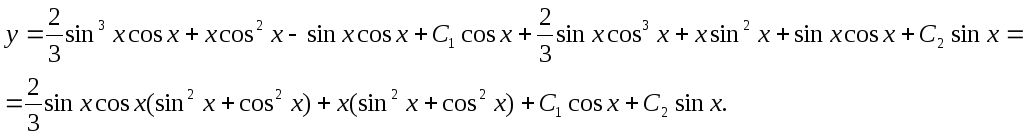
Окончательный ответ:

Вообще говоря, метод вариации произвольных постоянных пригоден для нахождения решений любого линейного неоднородного уравнения. Но т.к. нахождение фундаментальной системы решений соответствующего однородного уравнения может быть достаточно сложной задачей, этот метод в основном применяется для неоднородных уравнений с постоянными коэффициентами.

3. Уравнения с правой частью специального вида

Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения.

Различают следующие случаи:

I. Правая часть линейного неоднородного дифференциального уравнения имеет вид:

где - многочлен степени m.

Тогда частное решение ищется в виде:

Здесь Q(x)- многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число  является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.

Пример. Решить уравнение .

Решим соответствующее однородное уравнение:

Теперь найдем частное решение исходного неоднородного уравнения.

Сопоставим правую часть уравнения с видом правой части, рассмотренным выше.

Частное решение ищем в виде: , где

Т.е.

Теперь определим неизвестные коэффициенты А и В.

Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.

Итого, частное решение:

Тогда общее решение линейного неоднородного дифференциального уравнения:

II. Правая часть линейного неоднородного дифференциального уравнения имеет вид:

Здесь Р₁(х) и Р₂(х) – многочлены степени m₁ и m₂ соответственно.

Тогда частное решение неоднородного уравнения будет иметь вид:

где число r показывает сколько раз число является корнем характеристического уравнения для соответствующего однородного уравнения, а Q₁(x) и Q₂(x) – многочлены степени не выше m, где m- большая из степеней m₁ и m₂.

Сводная таблица видов частных решений

для различных видов правых частей

N	Правая часть дифф.уравнения	Корни характеристиче­ского уравнения	Виды частного решения
I.		1. Число не явля­ется корнем ха­рактеристиче­ского уравнения
		2. Число – корень характеристиче­ского уравнения кратности
II.		1. Число не яв­ляется корнем характеристиче­ского уравнения
		2. Число явля­ется корнем ха­рактеристиче­ского уравнения кратности
III.		1. Числа не являются кор­нями характери­стического урав­нения кратности
		2. Числа яв­ляются корнями характеристиче­ского уравнения кратности
IV.		1. Числа не являются кор­нями характери­стического урав­нения кратности
		2. Числа являются кор­нями характери­стического урав­нения кратности

Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.

Т.е. если уравнение имеет вид: , то частное решение этого уравнения будет где у₁ и у₂ – частные решения вспомогательных уравнений

и

Для иллюстрации решим рассмотренный выше пример другим способом.

Пример. Решить уравнение

Правую часть дифференциального уравнения представим в виде суммы двух функций f₁(x) + f₂(x) = x + (-sinx).

Составим и решим характеристическое уравнение:

1. Для функции f₁(x) решение ищем в виде .

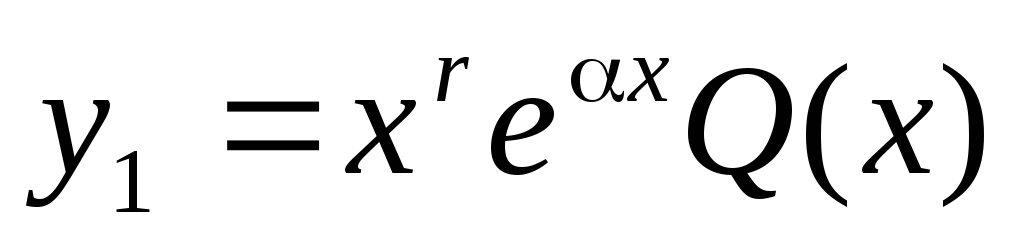Получаем: Т.е.

Итого:

Т.е. искомое частное решение имеет вид:

Общее решение неоднородного дифференциального уравнения:

Рассмотрим примеры применения описанных методов.

Пример 1.. Решить уравнение

Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:

Общее решение однородного уравнения:

Теперь найдем частное решение неоднородного уравнения в виде:

Воспользуемся методом неопределенных коэффициентов.

Подставляя в исходное уравнение, получаем:

Частное решение имеет вид:

Общее решение линейного неоднородного уравнения:

Пример. Решить уравнение

Характеристическое уравнение:

Общее решение однородного уравнения:

Частное решение неоднородного уравнения: .

Находим производные и подставляем их в исходное неоднородное уравнение:

Получаем общее решение неоднородного дифференциального уравнения: