ЛЕКЦИЯ

по учебной дисциплине

МАТЕМАТИКА

Тема .Функции нескольких переменных

Лекция 14. Дифференцируемость функций нескольких переменных

Учебные и воспитательные цели

1. Изучить основные понятия дифференцируемости и полного дифференциала функции нескольких переменных, ввести понятия частных производных высших порядков и дифференциалов высших порядков, рассмотреть вопрос дифференцирования сложных и неявных функций.

2. Развивать математическое и логическое мышление, повышать математическую культуру.

Учебные вопросы и расчет времени

I. Введение 3 мин

II. Основная часть 85 мин

Учебные вопросы

1. Дифференцируемость и полный дифференциал функции 30 мин

2. Частные производные и дифференциалы высших порядков 20 мин

3. Производная сложной функции 15 мин

4. Дифференцирование неявной функции 20 мин

III. Заключение 2 мин

Введение

Функции одной переменной не охватывают все зависимости, существую-щие в природе. Поэтому естественно расширить известное понятие функцио-нальной зависимости и ввести понятие функции нескольких переменных. Введем для функции нескольких переменных понятия, которые аналогичны понятиям функции одной переменной: производная, дифференцируемость, частные производные высших порядков, правила дифференцирования сложных функций и функций, заданных неявно.

1. Дифференцируемость и полный дифференциал функции

Пусть функция определена в некоторой окрестности точки. Составим полное приращение функции в точке М:

Функция называется дифференцируемой в точке, если её полное приращение в этой точке можно представить в виде

(1)

где ипри,. Сумма первых двух слагаемых в равенстве (1) представляет собойглавную часть приращения функции..

Главная часть приращения функции , линейная относительнои, называетсяполным дифференциалом этой функции и обозначается символом:

(2)

Выражения иназывают частными дифференциалами. Для независимых переменныхх иу полагаюти. Поэтому равенство (2) можно переписать в виде

(3)

Теорема 1 (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке М(х,у), то она непрерывна в этой точке, имеет в ней частные производные и, причем

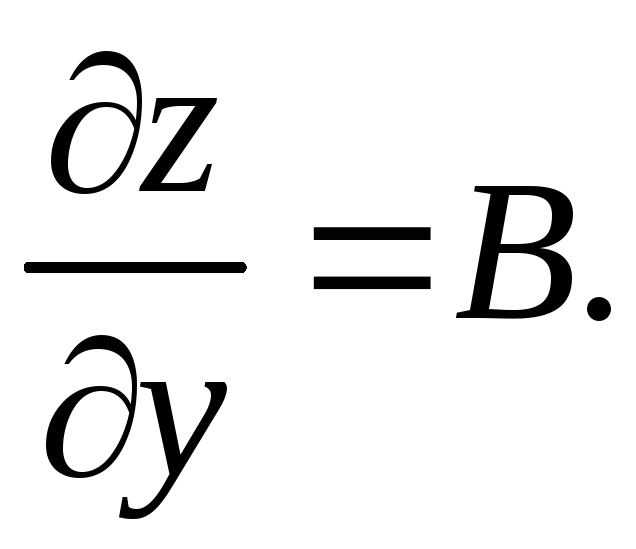
Так как функция дифференцируема в точке М, то имеет место равенство (1). Отсюда вытекает, что 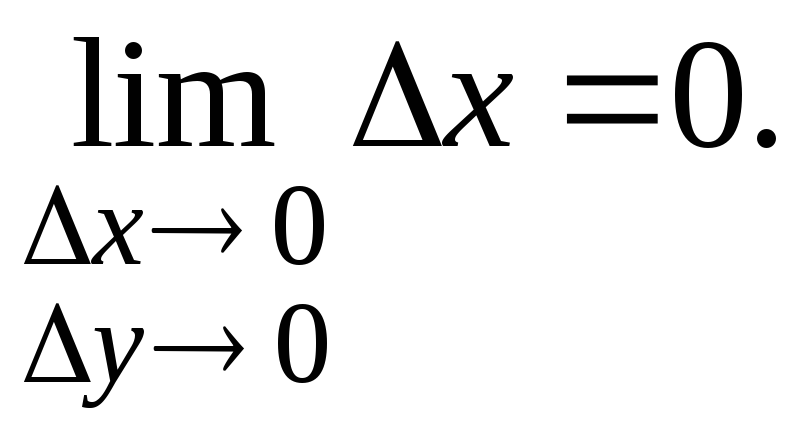Это означает, что функция непрерывна в точке М. Положивв равенстве (1), получим:Отсюда находимПереходя к пределу при, получим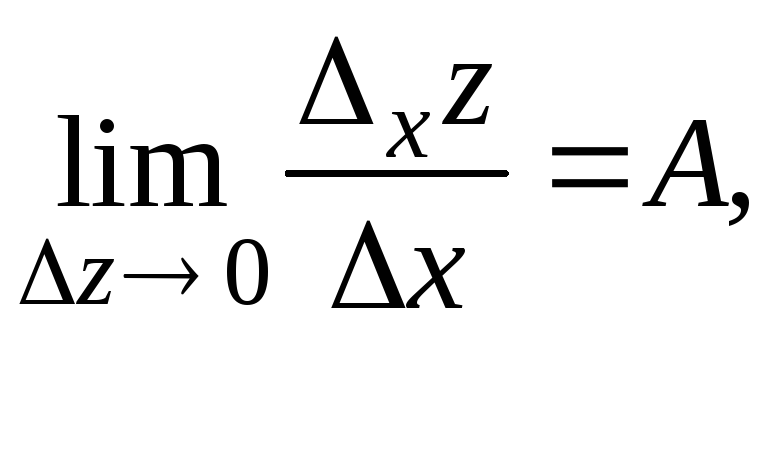т. е.Таким образом, в точке М существует частная производнаяАналогично показывается, что в точке М существует частная производная

Равенство (1) можно записать в виде

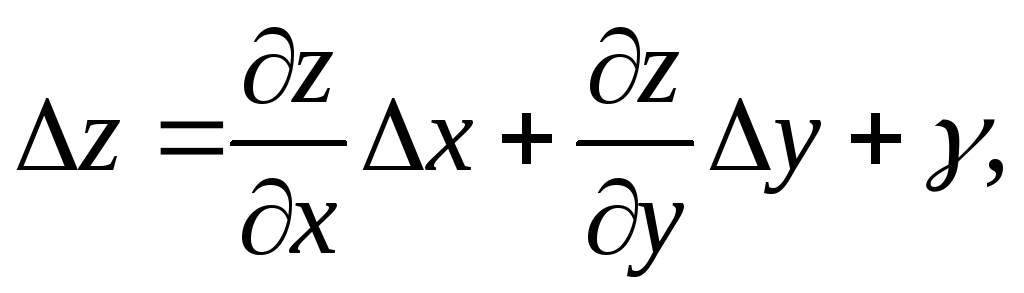(4)

где при,.

Отметим, что обратное утверждение не верно, т. е. из непрерывности функции или существования частных производных не следует дифференцируемость функции. Так, непрерывная функция не дифференцируема в точке (0;0).

Как следствие теоремы получаем формулу для вычисления полного дифференциала. Формула (3) принимает вид:

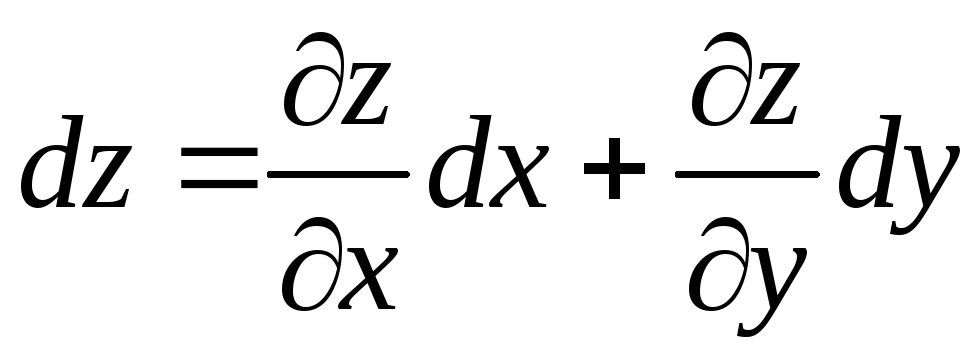(5)

или

где 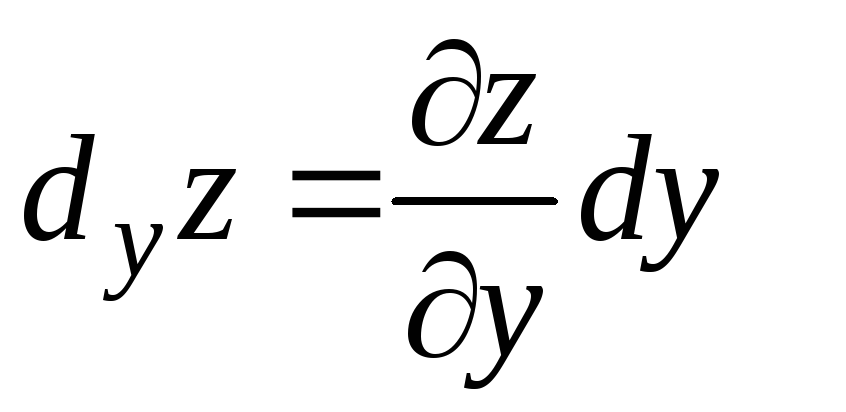– частные дифференциалы функции.

Теорема 2 (достаточное условие дифференцируемости функции). Если функция имеет непрерывные частные производныеив точкеМ(х, у), то она дифференцируема в этой точке и её полный дифференциал выражается формулой (5).

Примем теорему без доказательств.

Отметим, что для функции одной переменной существование производнойв точке является необходимым и достаточным условием её дифференцируемости в этой точке.

Чтобы функция была дифференцируема в точке, необходимо, чтобы она имела в ней частные производные, и достаточно, чтобы она имела в точке непрерывные частные производные.

Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциала функции двух (и большего числа) переменных.

Из определения дифференциала функции следует, что при достаточно малыхиимеет место приближенное равенство

. (6)

Так как полное приращение равенство (6) можно переписать в следующем виде:

(7)

Формулой (7) пользуются в приближенных расчетах.

Пример 1.1. Вычислить приближенно 1,02^3,01 .

Решение. Рассмотрим функцию Тогда 1,02^3,01 = (х+х)^у+у, где х =1, х = 0,02, у = 3, у = 0,01. Воспользуемся формулой (7), предварительно найдя :Следовательно,

1,02^3,01 = 1³ +31^3-1 0,02 + 1³ln10,01, т. е. 1,02^3,01  1,06.

Доля сравнения: используя микрокалькулятор, находим 1,02^3,01  1,061418168.

Отметим, что с помощью полного дифференциала можно найти: границы абсолютной и относительной погрешностей в приближенных вычислениях; приближенное значение полного приращения функции и т. д.