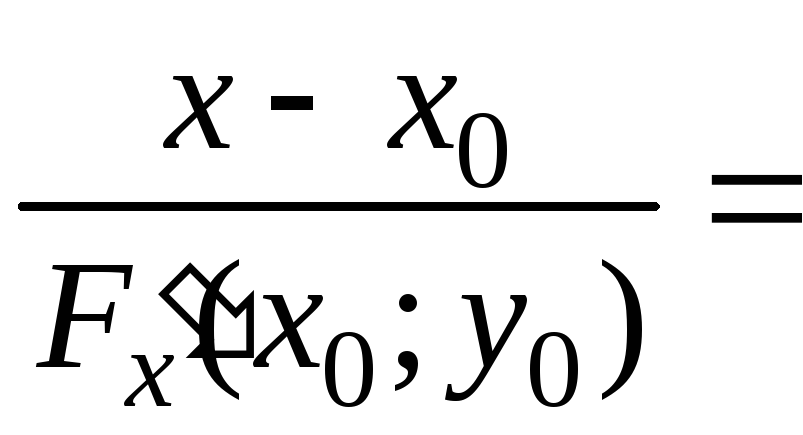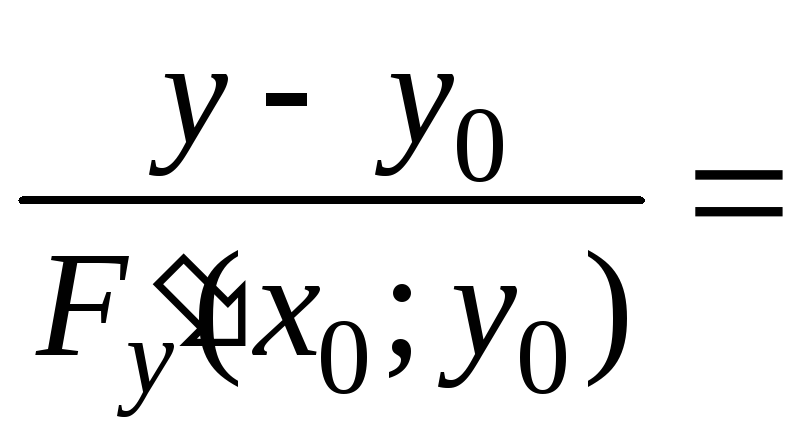- •Учебные и воспитательные цели
- •Учебные вопросы и расчет времени
- •Учебные вопросы
- •Функция называется дифференцируемой в точке, если её полное приращение в этой точке можно представить в виде
- •Главная часть приращения функции , линейная относительнои, называетсяполным дифференциалом этой функции и обозначается символом:
- •Выражения иназывают частными дифференциалами. Для независимых переменныхх иу полагаюти. Поэтому равенство (2) можно переписать в виде
- •Частные производные и дифференциалы высших порядков
- •Методом математической индукции можно показать, что
- •Производная сложной функции
- •Дифференцирование неявной функции Функция называетсянеявной, если она задается уравнением
Дифференцирование неявной функции Функция называетсянеявной, если она задается уравнением
![]() , (11)
, (11)
неразрешенным
относительно z.
Найдем частные производные
 неявной функцииz,
заданной уравнением (11). Для этого,
подставив в уравнением вместо z
функцию
неявной функцииz,
заданной уравнением (11). Для этого,
подставив в уравнением вместо z
функцию ![]() получим тождество
получим тождество![]() .Частные производные
по х
и по у
функции, тождественно равной нулю, также
равны нулю:
.Частные производные
по х
и по у
функции, тождественно равной нулю, также
равны нулю:
![]()
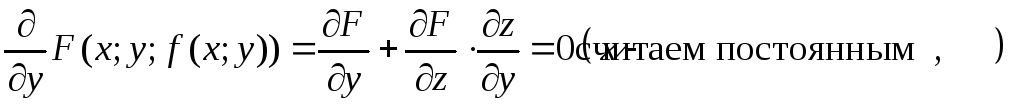
откуда

 (12)
(12)
Замечания.
а) Уравнение вида
(11) не всегда определяет одну переменную
как неявную функцию двух других. Так,
уравнение
![]() определяет
функции
определяет
функции![]() и
и![]() ,
определенные в круге
,
определенные в круге![]() ,
и
,
и![]() определенную в полукруге
определенную в полукруге![]() при
при![]() и т. д., а уравнение
и т. д., а уравнение![]() не определяет никакой функции.
не определяет никакой функции.
Имеет место теорема существования неявной функции двух переменных:
если функция
![]() и её производные
и её производные![]() и
и![]() ,
,![]() определены и непрерывны в некоторой
окрестности точки
определены и непрерывны в некоторой
окрестности точки![]() ,
причем
,
причем![]() ,
а
,
а![]() ,
то существует окрестность точки М0,
в которой уравнение (11) определяет
единственную функцию
,
то существует окрестность точки М0,
в которой уравнение (11) определяет
единственную функцию ![]() ,непрерывную и
дифференцируемую в окрестности точки
,непрерывную и
дифференцируемую в окрестности точки
![]() и такую, что
и такую, что![]() .
.
б) Неявная функция
![]() одной переменной задается уравнением
одной переменной задается уравнением![]() .
Можно показать, что в случае, если
удовлетворены условия существования
неявной функции одной переменной
(имеется теорема, аналогичная
вышеуказанной), то производная неявной
функции находится по формуле
.
Можно показать, что в случае, если
удовлетворены условия существования
неявной функции одной переменной
(имеется теорема, аналогичная
вышеуказанной), то производная неявной
функции находится по формуле
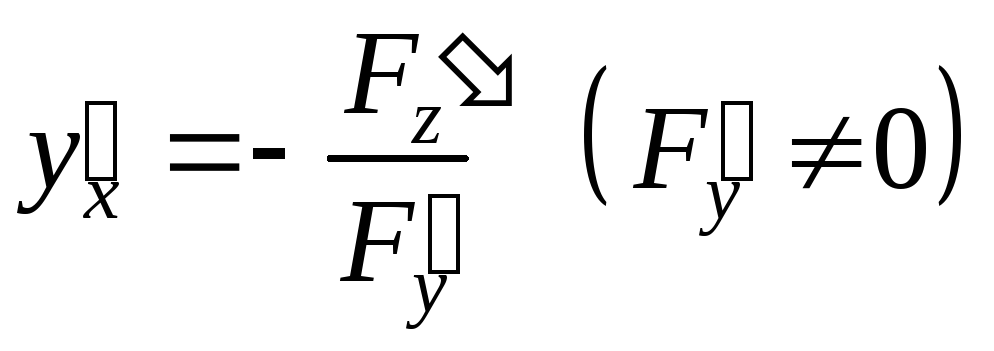 .
.
Пример 4.1.
Найти частные производные функции z,
заданной уравнением
![]()
Решение.
Здесь
![]()
![]() ,
,![]()
![]()
![]() По формулам (12) имеем:
По формулам (12) имеем:![]()
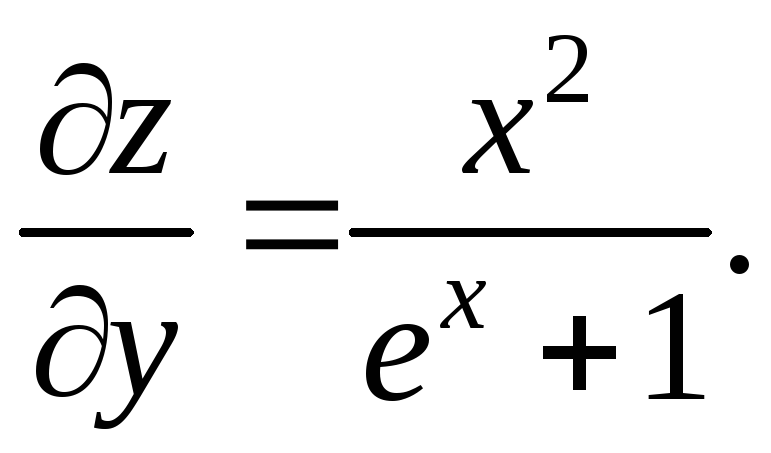
Пример 4.2.
Найти
![]() если неявная функция
если неявная функция![]() задана уравнением
задана уравнением![]()
Решение.
Здесь
![]() Следовательно,
Следовательно,
Если поверхность
S
задана уравнением
![]() ,
то уравнения (2) и (3), с учетом того, что
частные производные могут быть найдены
как производные неявной функции
,
то уравнения (2) и (3), с учетом того, что
частные производные могут быть найдены
как производные неявной функции

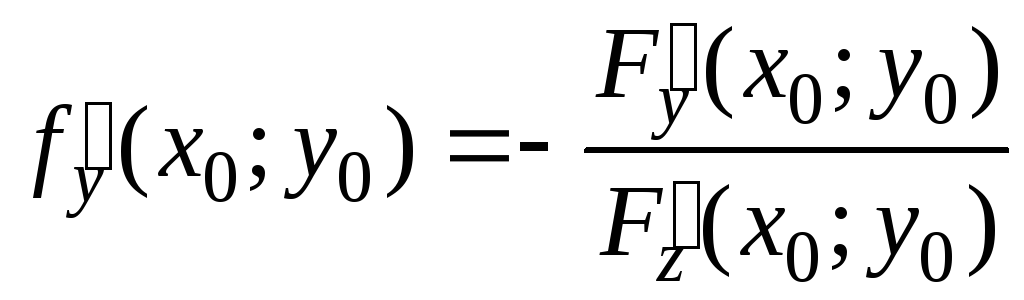
(см. формулы (12)), примут соответственно вид
![]()
![]()
![]()
и