1. Нечеткие множества.

Пусть имеется универсальное (под)множество Х, а все остальные множества являются его подмножествами.

Пусть , Определим функцию следующим образом:

Функцию будем называть характеристической функцией множества. Любая такая ф-ция задает множество.

Пусть функция F(x) принимает любые значения из [0,1]. Тогда она будет называться функцией принадлежности, а ее значение μ(x) будем называть степень принадлежности элементаxнечеткому множествуF.

Для универсального множества μ(х) ≡ 1. Для пустого множества μ(х) ≡ 0.

Носителем нечеткого множества A будем называть такое множество, которое содержит только те элементы множества A, степень принадлежности которых > 0.

Множество α-уровня – множество элементов А_α, степень принадлежности которых > α.

ТВГ h_α функциипринадлежности множества А называется высотой нечеткого множества.

Высота нечеткого множества всегда существует и равна какому-то числу из [0;1].

Нечеткое множество A называется субмодальным, если h_α =1, но не существует такого x, для которого μ(x) = 1.

Функция принадлежности называется унимодальной на интервале [а;b], если она непрерывна на [а;b], а также существует интервал [c,d]⊂[a;b], такой, что μ(х) строго монотонно возрастает на [a;c], монотонно убывает на [d;b] и принимает свое максимальное значение на [c;d]. Если [c;d] вырождается в точку, то говорят, что функция принадлежности строго унимодальна.

Нечеткое множество называется унимодальным, если его функция принадлежности унимодальна.

Ядром нечеткого множества называется такое обычное множество его элементов, для которых μ(х) = 1.

Если нечеткое множество не является нормальным, то его ядро будет пустым. Поскольку h_α всегда существует, то непустое нечеткое множество можно преобразить к субнормальному, поделив значение функции принадлежности на высоту h_α. Тогда ТВГ=1

Границами нечеткого множества называется такие элементы, для которых значения функции принадлежности отличны от 0 и 1.

2. Основные виды функции принадлежности.

1. Треугольная.

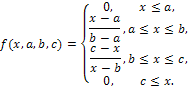
Определяет треугольник, причем a,c - основание, b - вершина.

В данном случае интервал [a,c] - носитель множества, [a,b] и [b,c] - границы, b - ядро.

2. Трапециевидная.

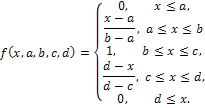
Эти две функции характеризую такие свойства, как “≈”, “похож на” и т.д.

3. Z-образная кривая.

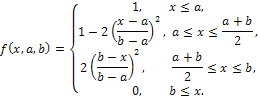
Параметры a и b определяют вид кривой. В данном случае мы имеем нормально выпуклое нечеткое множество, у которого ядро - , носитель - .

4. S-образная кривая.

В данном случае ядро - , носитель - .

3. Операции над нечеткими множествами.

Нечеткое множество является обобщением классического множества. Обобщать операции можно по-разному => определение операций будет неоднозначным, т.е. одну и ту же операцию можно определить по-разному.

Говорить об операциях над нечет. множествами возможно только, если все они проводятся на одном и том же универсальном множестве.

Т.к. неч. множество полностью определяется своей функцией принадлежности, множество и функция явл. по сути синонимами. Но одно и то же свойство может быть задано с помощью различных функций принадлежности.

Рассмотрим отношение равенства: два нечетких множества называются равными, если для их функции принадлежности равны: , A = B.

Нечеткое множество А называется множеством нечеткого множества, если для . .

Если для двух множеств неверно ни , ни , то говорят, что множества A и B несравнимы.

Пересечением двух нечетких множеств будем называть некоторое нечеткое множество C (), функция принадлежности которого определяется так: .

Объединением двух нечетких множеств A и B, заданных на одном и том же универсальном множестве, называется множество C () определяется как: .

Симметрической разностью нечетких множеств A и B, заданных на одном и том же универсальном множестве, называется множество C, функция принадлежности которого определяется так: .

Дополнением нечеткого множества A называется множество .

В системе MatLab при моделировании именно эти определения стоят по умолчанию.

Для этих операций выполняются свойства:

1. 

2. 

3. 

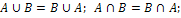
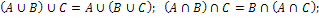
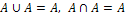4. - идемпотентность;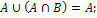

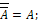
5. 

6. 

7. 

8. 

Принципиальной особенностью нечетких множеств является то, что для них не выполняются два свойства, характерные для классических множеств:

1. 

2. 

Введенные определения наиболее приближают алгебру нечетких множеств к булевым. В других определениях некоторые из 8 свойств не выполняются.

В ряде конкретных случаев целесообразно использовать не основные операции с нечеткими множествами, а альтернативные. Это может быть вызвано желанием, например, повысить адекватность модели.