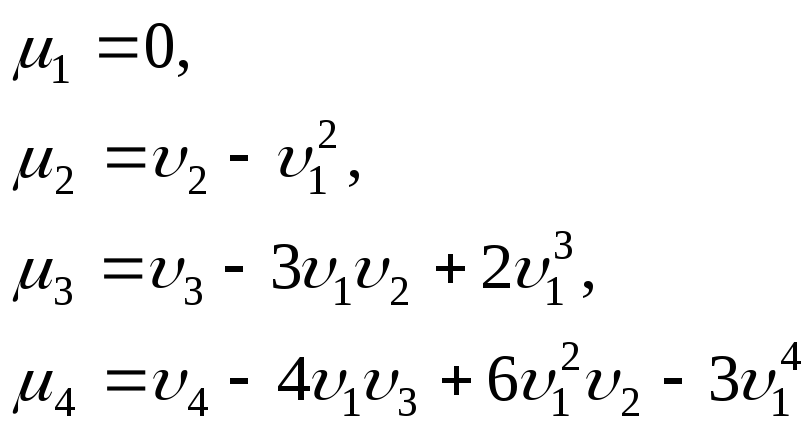- •Теория вероятностей
- •I. Программа курса «теория вероятностей и математическая статистика»
- •Раздел I. Теория вероятностей.
- •Тема 1. Основные понятия теории вероятностей. Предмет курса.
- •Тема 2. Зависимые и независимые случайные события. Основные формулы умножения и сложения вероятностей.
- •Тема 3. Повторные независимые испытания по схеме Бернулли.
- •Тема 4. Одномерные случайные величины и их характеристики.
- •Тема 5. Многомерные случайные величины и их свойства.
- •Тема 6. Функции случайных величин.
- •Раздел II. Математическая статистика.
- •Тема 11. Элементы математической статистики. Выборочный метод.
- •Тема 12. Статистические оценки параметров генеральной совокупности. Статистические гипотезы.
- •Тема 13. Элементы дисперсионного анализа.
- •Тема 14. Элементы теории регрессии и корреляции.
- •II. Методические указания предмет теории вероятностей
- •Случайным называют событие, которое при осуществлении совокупности условий s может либо произойти, либо не произойти.
- •Виды случайных событий
- •Операции над событиями
- •Классическое определение вероятности
- •Геометрическая вероятность
- •Элементы комбинаторики
- •I. Перестановки
- •II. Размещения
- •III. Сочетания
- •Теоремы сложения и умножения вероятностей
- •Формула полной вероятности. Формулы бейеса
- •Повторные независимые испытания. Испытания по схеме бернулли
- •Случайные величины и законы их распределения
- •Числовые характеристики случайных величин
- •Законы распределения случайных величин
- •Системы двух случайных величин
- •Функция двух случайных аргументов
- •Элементы математической статистики
- •III. Контрольные задания
- •IV. Приложения
- •Элементы комбинаторики
- •Дискретные и непрерывные случайные величины
- •V. Тесты
- •Тема: Виды случайных событий, классическое определение вероятности, элементы комбинаторики
- •Тема: Теоремы сложения и умножения вероятностей
- •Тема: Случайные независимые испытания по схеме Бернулли
- •Тема: Одномерные случайные величины
- •VI. Литература
- •Содержание
- •I. Программа курса 4
- •II. Методические указания 6
- •III. Контрольные задания 34
Элементы комбинаторики
|
Комбинации |
Логическая схема комбинации |
Формула числа комбинаций |
|
это комбинации из n элементов, которые отличаются друг от друга только порядком элементов. |
|
|
|
это комбинации из n элементов по k элементов, которые отличаются друг от друга или самими элементами, или порядком элементов. |
|
|
|
Сочетания это все возможные комбинации из n элементов по k элементов, которые отличаются друг от друга, по крайней мере, хотя бы одним элементом. |
|
|
Приложение 4
СХЕМА БЕРНУЛЛИ
I. Пусть производится n независимых испытаний, в каждом из которых вероятность события А постоянна и равна р. Вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз.
|
№ |
Значения n и р |
Формула |
|
1. |
при любом
|
Формула Бернулли:
где
|
|
2. |
|
Локальная теорема Лапласа:
где
Значения
|
|
3. |
( |
Формула Пуассона:
где
|
II.
Пусть
производится n
независимых испытаний, в каждом из
которых вероятность события А
постоянна и равна р.
Вычислить вероятность того, что при n
испытаниях событие А
осуществится не менее k1
и не более
k2
раз (причем
![]() ,
,![]() ).
).
Интегральная теорема Лапласа:
![]() ,
,
где
![]() ,
,![]() ;
;
Значения
![]() находят по таблице.
находят по таблице.
III. Наивероятнейшее число появления события А в n независимых испытаниях k0:
![]() ,
,
k0 – целое.
Приложение 5
Дискретные и непрерывные случайные величины
|
ДИСКРЕТНЫЕ СВ |
НЕПРЕРЫВНЫЕ СВ | ||||||||||
|
Способы задания | |||||||||||
Функция распределения дискретной случайной величины является ступенчатой, сохраняющей постоянное значение на каждом интервале. |
Дифференциальная функция обладает свойством:
| ||||||||||
|
Числовые характеристики | |||||||||||
|
Математическое ожидание | |||||||||||
|
|
| ||||||||||
|
Дисперсия
| |||||||||||
|
|
| ||||||||||
|
Среднее квадратическое отклонение
| |||||||||||
|
Начальный момент порядка k
| |||||||||||
|
|
| ||||||||||
|
Центральные моменты
| |||||||||||
|
Коэффициент асимметрии
| |||||||||||
|
Эксцесс
| |||||||||||
|
Мода | |||||||||||
|
|
| ||||||||||
|
Медиана | |||||||||||
|
|
| ||||||||||

 Перестановки
Перестановки
 Размещения
Размещения