Системы двух случайных величин

Двумерной называют случайную величину , возможными значениями которой являются пары чисел. Составляющиеи, рассматриваемые одновременно, образуютсистему двух случайных величин.

Дискретной называют двумерную случайную величину, составляющие которой дискретны.

Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, т.е. пар чисел и их вероятностей,. Обычно закон распределения задают в виде таблицы с двойным входом:

Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. Для того чтобы найти вероятность , надо просуммировать вероятности «столбца». Сложив вероятности «строки», получим вероятность.

Корреляционным моментом случайных величининазывают математическое ожидание произведения отклонений этих величин:

.

Для вычисления корреляционного момента дискретных величин используют формулу:

,

где

Корреляционный момент служит для характеристики связи между величинами и. Для независимых случайных величиникорреляционный момент равен нулю:.

Коэффициентом корреляции случайных величининазывают отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

.

Если случайные величины инезависимые, то коэффициент корреляции равен нулю. В общем случае.

Пример. Распределение вероятностей дискретной двумерной случайной величины задано таблицей:

	3	8	10
4
5

Найти: 1) законы распределения составляющих и;

2) математические ожидания и дисперсии составляющих;

3) коэффициент корреляции .

Решение. 1) Сложив вероятности «по столбцам», получим вероятности возможных значений :;;.

Составим закон распределения составляющей :

	3	8	10

Контроль: .

Сложив вероятности «по строкам», найдем распределение составляющей :

	4	5
	0,55	0,45

Контроль: .

2) Найдем математическое ожидание и дисперсию величины :

;

.

Найдем математическое ожидание и дисперсию величины :

;

.

3) По определению коэффициента корреляции

Найдем корреляционный момент случайных величинии их средние квадратические отклонения:

,

откуда .

Подставим найденные значения в получим:

.

Функция двух случайных аргументов

Если каждой паре возможных значений случайных величин исоответствует одно возможное значение случайной величины, тоназываютфункцией двух случайных аргументов ии пишут:

.

Если и– дискретные независимые случайные величины, то для того, чтобы найти распределение функции, надо найти все возможные значения, для чего достаточно сложить каждое возможное значениесо всеми возможными значениями; вероятности же найденных значенийравны произведениям вероятностей складываемых из значенийи.

Пример. Дискретные независимые случайные величины заданы распределениями:

	1	3				2	4
	0,4	0,6				0,8	0,2

Составить распределение случайной величины .

Решение. Возможные значения есть суммы каждого возможного значениясо всеми возможными значениями:

.

Найдем вероятности этих возможных значений.

Для того чтобы , достаточно, чтобы величинаприняла значениеи величина– значение. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равны 0,4 и 0,8.

Аргументы инезависимы, поэтому событияинезависимы и, следовательно, вероятность их совместного наступления (т.е. вероятность события) по теореме умножения равна.

Аналогично найдем:

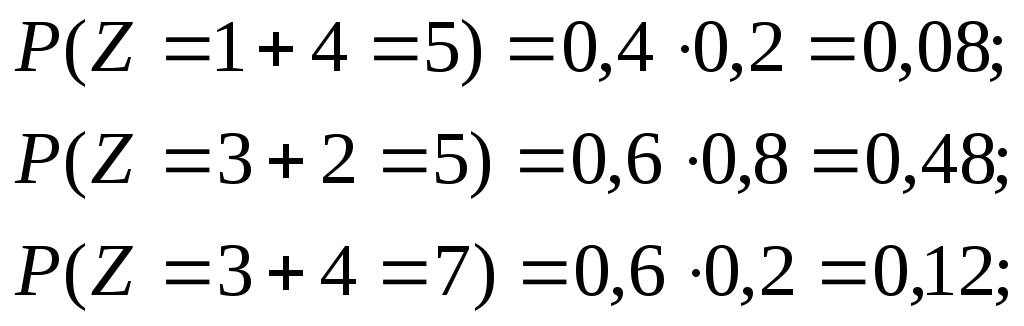
запишем искомое распределение, сложив предварительно вероятности несовместных событий :

	3	5	7
	0,32	0,56	0,12

Контроль: .

Пусть инепрерывные независимые случайные величины, тогда дифференциальная функциясуммы(при условии, что дифференциальная функция хотя бы одного из аргументов задана в интервалеодной формулой) может быть найдена по формуле

,

либо по равносильной формуле

,

где и– дифференциальные функции аргументов.

Если возможные значения аргументов неотрицательны, то дифференциальную функцию величинынаходят по формуле

,

либо равносильной формуле

.

Плотность распределения суммы независимых случайных величин называют композицией.