
- •3. Обратная задача теории погрешностей и ее решение методом равных влияний
- •Часть 2 1. Апроксимация – замена одной функции другой, более близкой к исходной и обладающей хорошими свойствами(лёгкость выполнения аналитических данных и вычислительных операций)
- •Interp,
- •Interp.
- •Часть 3.
- •Линеаризация данных по методу наименьших квадратов.
- •4. Кусочно-линейное и кусочно-квадратичное интерполирование
- •Часть 4.
- •3. Квадратурные формулы Ньютона – Котеса
- •4. Квадратурная формула Гаусса
- •5. Метод Монте-Карло
- •Часть 5.
4. Кусочно-линейное и кусочно-квадратичное интерполирование
Иногда, интерполирование по всей совокупности точек бывает недостаточным. В этих случаях можно воспользоваться объединением фрагментов графиков полиномов низкой степени и интерполированием между последовательными узлами. Самый простой в использовании полином первой степени. Он создает ломаную, состоящую из отрезков, которые проходят через две точки. Чтобы представить эту кусочно-линейную кривую, используется полином Лагранжа

или формула угла наклона отрезка линии в точке
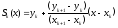 ,
,
где
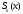 – линейный сплайн на отрезке [xk+1,
xk],
yk
– заданное значение функции, полученное
экспериментально в заданных узлах.
Аналогично можно построить
кусочно-квадратичный полином.
– линейный сплайн на отрезке [xk+1,
xk],
yk
– заданное значение функции, полученное
экспериментально в заданных узлах.
Аналогично можно построить
кусочно-квадратичный полином.
5. Суть процедуры сглаживания состоит в подмене данной функции на каждом из рассматриваемых отрезков наилучшим линейным среднеквадратичным приближением.
На
первом этапе для таблично заданной
функции найти такую функцию S(x),
составленную из линейных функций
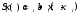 ,
чтобы
,
чтобы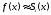 для всехх
в смысле минимума квадрата отклонений,
т.е.
для всехх
в смысле минимума квадрата отклонений,
т.е.
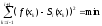 .
В результате решается задача нахождения
коэффициентовai,
bi
методом наименьших квадратов:
.
В результате решается задача нахождения
коэффициентовai,
bi
методом наименьших квадратов:
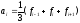 ,
,

Второй
этап состоит в пересчете данной таблицы
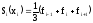 для
для .
Доопределим новую табличную функцию
значениями
.
Доопределим новую табличную функцию
значениями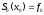 и
и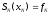 .
В результате этого получаем новую
табличную функцию, в которой сохраняется
характер поведения исходной функции.
Описанная процедура называется
осреднением по трем точкам и является
простым частным случаем линейного
фильтра.
.
В результате этого получаем новую
табличную функцию, в которой сохраняется
характер поведения исходной функции.
Описанная процедура называется
осреднением по трем точкам и является
простым частным случаем линейного
фильтра.
6. Леммы о сплайнах.
Смыкающий (чертежный) сплайн. Существует единственный кубический сплайн, который имеет первую производную с граничными условиями
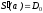 ,
,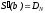 ,
т.е. смыкающий сплайн имеет определенный
наклон в крайних точках.
,
т.е. смыкающий сплайн имеет определенный
наклон в крайних точках.Естественный сплайн. Существует единственный кубический сплайн со свободными граничными условиями
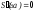 ,
, ,
т.е. сплайн допускает свободный наклон
на краях для обеспечения положения,
которое минимизирует осцилляцию кривой.
,
т.е. сплайн допускает свободный наклон
на краях для обеспечения положения,
которое минимизирует осцилляцию кривой.Экстраполяционный сплайн. Существует единственный кубический сплайн, который используется для экстраполирования по внутренним узлам, чтобы определить
 по
узламх1,
х2
и
по
узламх1,
х2
и
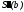 по узлам
хN-1,
хN-2.
по узлам
хN-1,
хN-2.
Сплайн, заканчивающийся параболой. Существует единственный кубический сплайн, такой, что
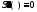 на
интервале [x0,
x1]
и
на
интервале [x0,
x1]
и
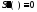 на
интервале [xN-1,
xN].
на
интервале [xN-1,
xN].Сплайн с заданной кривизной в крайних точках. Существует единственный кубический сплайн с заданными значениями второй производной в крайних точках.
Часть 4.
1.
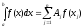 . (1)
. (1)
Формула
(1) называется формулой механических
квадратур,
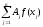 – квадратурной суммой,Аj
– квадратурными коэффициентами, хj
– узлами или абсциссами квадратурного
правила.
– квадратурной суммой,Аj
– квадратурными коэффициентами, хj
– узлами или абсциссами квадратурного
правила.
Остаточным членом квадратурного правила называется величина
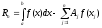 .
.
2. Пусть заданы значения подынтегральной функции f(x) в точках x0, x1, , xn принадлежащих [a,b], тогда для f(x) строят интерполяционный многочлен Лагранжа n-ой степени, т.е.
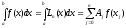 ,
где
,
где
 . (3)
. (3)
Формула (3) называется интерполяционной квадратурной формулой. Ее остаточный член
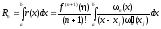 , (4)
, (4)
где – некоторая точка [a,b].
Если узлы квадратурного правила равноотстоящие, то квадратурные коэффициенты принимают вид
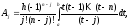 (5)
(5)
где
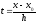 ,
,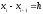 ,
,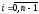 .
.
