
- •1 Основные теоретические сведения
- •1.1.1 Прогнозирование и планирование как функция менеджмента
- •1.1.2 Обзор техники и видов планирования
- •1.1.3 Примеры планирования, на базе деловой компьютерной игры БК: Максимум
- •1.2 Методы макроэкономического планирования и прогнозирования
- •1.2.1 Организация прогнозирования и планирования
- •1.2.2 Федеральные целевые программы
- •2 Методы и модели в принятии управленческих решений
- •2.1 Принятие решений в условиях полной определенности
- •2.1.1 Многокритериальные методы оптимизации
- •2.2 Модели оценки социального и экономического развития регионов
- •3 Прогнозирование
- •3.1 Оценка и прогнозирование спроса
- •3.2 Оценка и прогнозирование спроса на основе экстраполяции
- •3.2.1 Прогнозирование с помощью абсолютных приростов
- •3.2.2 Прогнозирование с помощью относительных приростов
- •3.2.3 Прогнозирование с помощью индексов
- •3.2.4 Адаптивные методы прогнозирования
- •3.3 Оценка и прогнозирование спроса с помощью моделирования
- •3.3.1 Прогнозирование на основе трендовых моделей
- •3.3.2 Прогнозирование на основе однофакторных моделей
- •3.3.3 Прогнозирование с учетом сезонных эффектов
- •4 Основные разделы комплексного планирования (в рамках производственной программы)
- •4.1 Планирование подготовки производства
- •4.1.1 Планирование потребности в материалах
- •4.1.2 Планирование затрат на приобретение материалов
- •4.2 Планирование производственной программы
- •4.2.1 Детерминированные модели согласования объемов производства и спроса на продукцию предприятия
- •4.2.2 Расчет базовой цены товара
- •4.3 Прогнозирование и индикативное планирование развития комплексов, отраслей и сфер национальной экономики
- •4.3.2 Прогнозирование развития материального производства
- •4.3.3 Прогнозирование социального развития
- •4.3.4 Планирование доходов и расходов государства
- •4.3.5 Планирование производства в государственном секторе
- •5 Вопросы к зачету
- •Список использованных источников

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
II |
|
JJ |
3.3Оценка и прогнозирование спроса с помощью моделирования
Основная идея прогнозирования на основе моделирования заключается в построении модели спроса, зависящего от различных факторов. Вычисление прогнозного значения объема спроса осуществляется на основе известных прогнозных значений факторов спроса. В общем случае спрос выражается обобщенной функцией спроса3:
QA = f(PA, PB, . . . , PZ , I ,W, N),
где QA — величина спроса на товар A, PA — цена товара A, PB, . . . , PZ — цены товаров-заменителей и сопутствующих товаров; I — доход покупателя, W — уровень благосостояния покупателя, его покупательская способность, N — степень новизны (насыщенности) товара A.
В случае, когда все факторы кроме одного неизменны, получаем однофакторную модель спроса. В частности, если считать, что спрос зависит только от цены данного товара, то функция спроса имеет вид QA = f (PA).
3Возможно иное представление обобщенной функции спроса.
Прогнозирование |
Стр. 83 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
II |
|
JJ |
Прогнозирование спроса на основе однофакторных моделей легко осуществлять средствами Excel. Предположим, что требуется спрогнозировать объем спроса на данном рынке на ближайшие периоды, и имеется один определяющий спрос фактор. Алгоритм решения данной задачи можно представить в виде следующих шагов.
1.Собрать сведения о значениях определяющего фактора и объемах реализации товара на рынке за несколько предшествующих периодов.
2.Занести эти данные в соседние столбцы таблицы Excel. (По горизонтальной оси нужно откладывать значения фактора — они вводятся в окне под именем «Значения X:». По вертикальной оси значения объемов спроса нужно вводить в окне под именем «Значения Y:»).
3.Построить диаграмму, тип диаграммы — «точечная».
4.К построенному графику добавить тренд, вывести уравнение тренда и степень аппроксимации R2.
5.Вывести другие тренды к данному графику и на основе коэффициентов детерминации R2 выбрать наилучший (с наибольшей степенью аппроксимации) тренд.
6.В выбранное уравнение тренда подставить предполагаемое значение фактора в прогнозируемом периоде и вычислить объем спроса.
Прогнозирование |
Стр. 84 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . .
Подбор оптимального тренда данного типа осуществляется на основе метода наименьших квадратов, суть которого заключается в минимизации суммы квадратов отклонений значений yˆ, полученных по модели (уравнению) yˆ = f(x), от наблюдаемых значений y.
Точность степени прогноза в первом приближении может быть оценена с помощью коэффициента детерминации R2: чем выше данный показатель (ближе к единице), тем точнее прогноз, но R2 не должен быть меньше 0,5 при числе наблюдений не менее 10. В упрощенной формулировке данный показатель можно рассматривать как степень соответствия показателей модели результатам наблюдений. В частности, если R2 < 0,7, то прогноз будет соответствовать действительности менее чем на 70%.
При прогнозировании с помощью модели необходимо знать прогнозное значение определяющего фактора. Это значение может быть получено экспертным путем, спрогнозировано (например с помощью экстраполяции) или запланировано (организация сама может планировать цену реализации продукта). Самый простой фактор для прогнозирования — это время и прогнозное значение фактора — это период, для которого вычисляется прогноз. В таком случае говорят о прогнозировании на основе трендовых моделей.
II JJ
Прогнозирование |
Стр. 85 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.1 II |
|
JJ |
3.3.1Прогнозирование на основе трендовых моделей
Пусть определяющим фактором спроса является время. Тогда для прогнозирования с помощью MS Excel достаточно построить диаграмму типа «График» или «Точечная», добавить к нему тренд и в параметрах тренда указать вывод уравнения тренда (а также степень аппроксимации тренда — коэффициент детерминации R2). По уравнению тренда могут быть вычислены прогнозы в любой момент времени. Обычно рекомендуют прогнозировать по тренду не далее, чем на треть имеющихся наблюдений (тенденция может измениться).
MS Excel предлагает следующие типы трендов, строящиеся на основе метода наименьших квадратов:
•y = a + bx — линейный,
•y = a · xb — степенной,
•y = a · ebx — экспоненциальный,
•y = a0 + a1x + a2x2 + . . . + anxn — полиномиальный степени n = 2, 3, 4, 5, 6,
•y = a + b ln x — логарифмический,
атакже сглаживание графика функции на основе линейной фильтрации (скользящего среднего).
Прогнозирование |
Стр. 86 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.1 II |
|
JJ |
Экономический смысл параметров трендов. Для трендовых моделей фактором x выступает время (период), поэтому в некоторых моделях параметр b приобретает конкретный смысл:
•В линейной модели y = a + bx параметр b указывает на среднее значение абсолютного прироста y за один период.
•В полиномиальной модели параметр a1 также указывает на среднее значение абсолютного прироста y, а параметр
a2 характеризует среднее значение ускорения прироста y за один период.
•В экспоненциальной модели y = a · ebx параметр b указывает на среднее значение относительного прироста y за один период.
Прогнозирование |
Стр. 87 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.1 II |
|
JJ |
Прогнозирование с помощью линейной трендовой модели дает результаты близкие к прогнозу, полученному с помощью метода абсолютных приростов, а прогнозирование с помощью экспоненциальной трендовой модели дает результаты близкие к прогнозу, полученному с помощью индексов. В обоих случаях предпочтительнее считаются трендовые модели, так как по методу абсолютных приростов и индексному методу результаты прогнозирования сильно зависят от последних наблюдений, которые могут быть существенно выше или ниже трендовых значений.
При прогнозировании с помощью полиномиального тренда нужно помнить, что степень полинома должна быть не выше третьей степени (использование полиномиальных трендов предполагает прогнозирование на основе так называемых кривых роста [5]). Более того, при таком прогнозировании необходимо аккуратно повышать степень полинома: при повышении степени качество модели должно существенно повышаться — коэффициент детерминации должен возрастать приблизительно на 0,05 или более4. Другое ограничение на использование полиномиального тренда — должно быть достаточное число наблюдений. Для построения качественной модели рекомендуют, чтобы число наблюдений превышало степень полинома (число факторов) по крайней мере в 5–7 раз [?].
4Полиномиальный тренд степени n является n-факторной моделью, поэтому повышение степени полинома означает введение дополнительного фактора. Если в модели влияние фактора на результативный показатель оказывается менее 5%, то такое влияние можно «списать» на статистическую ошибку. Более точный диагноз осуществляется путем проверки соответствующей статистической гипотезы.
Прогнозирование |
Стр. 88 из 164 |
|
J I |
|
J I x y × |
|
|
513,5 |
|
-1,90 |
-0,004 |
|
0,996 |
514,6 |
513,2 |
|
3.3.1 |
II |
|
Оглавление |
3.3 Оценка и прогнозирование спроса с . . . |
||||||||||
515,5 |
|
2,00 |
0,004 |
|
1,004 |
514,3 |
513,3 |
|
|
||
редне |
|
0,72 |
0,001 |
|
1,001 |
|
0,2 |
|
|
JJ |
|
|
|
|
|
|
Прогноз |
|
|
|
|
|
|
|
516,2 |
516,2 |
|
516,2 |
514,8 |
513,7 |
|
|
|
||
|
516,9 |
517,0 |
|
517,0 |
514,6 |
|
|
|
|
||
|
Пример 3.2. |
В условиях примера 3 найдем объем спро- |
|
||||||||
|
517,7 |
517,7 |
|
517,7 |
515,0 |
|
|
|
|
||
са на продукцию предприятия в ближайшие три периода на |
|
||||||||||
18,0основе трендовых моделей. |
|
|
|
|
|||||||
17,0 |
Решение. Воспользуемся представленным выше алгоритмом |
|
|||||||||
16,0 |
|
||||||||||
15,0построения однофакторных моделей в MS Excel. Построим гра- |
|
||||||||||
13,014,0фик спроса, при этом можно выбрать тип диаграммы «График» |
|
||||||||||
12,0или «Точечная». Добавим к графику поочередно пять трендов: |
|
||||||||||
11,0линейный, степенной, логарифмический, экспоненциальный и |
|
||||||||||
09,010,0полиномиальный степени 2. В параметрах к трендам укажем вы- |
|
||||||||||
вод уравнения тренда, коэффициент аппроксимации R2 и про- |
|
||||||||||
1 |
|
3 |
|
5 |
|
7 |
9 |
11 |
13 |
|
|
гнозСпросна 3 периода впередАбс. приростов. В результате получимОтн. приростовграфики как на |
|
||||||||||
Индексный |
|
|
Скол. среднего |
Эксп. сглаживания |
|
|
|||||
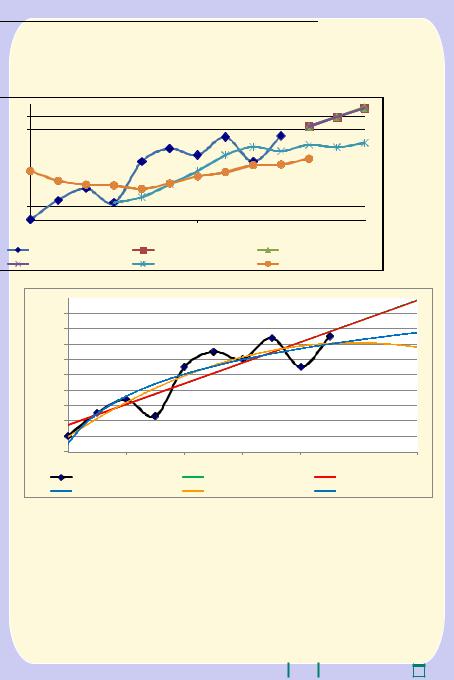
рисунке 3.2. |
|
|
|
|
|
|
|
|
|
||
518,0 |
y = 2,827ln(x) + 508,4 |
y = 508,5x0,005 |
|
|
|
|
|||||
517,0 |
|
|
|
|
|||||||
|
R² = 0,817 |
|
|
R² = 0,818 |
|
|
|
|
|||
516,0 |
|
|
|
|
|
|
|
||||
y = -0,063x2 + 1,372x + 507,6 |
|
|
|
|
|||||||
515,0 |
|
|
|
|
|||||||
|
R² = 0,842 |
|
|
|
|
|
|
||||
514,0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
513,0 |
|
|
|
|
|
|
|
y = 509,0e0,001x |
|
||
|
|
|
|
|
|
|
R² = 0,798 |
|
|
||
512,0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
511,0 |
|
|
|
|
|
|
|
y = 0,676x + 509,0 |
|
||
|
|
|
|
|
|
|
R² = 0,798 |
|
|
||
510,0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
509,0 |
|
|
|
|
|
|
|
|
|
|
|
508,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
5 |
7 |
9 |
11 |
13 |
|
|
|
Спрос |
|
|
|
Эксп. тренд |
|
Линейный тренд |
|
||
|
|
Логарифм. тренд |
|
|
Полином. тренд |
|
Степенной тренд |
|
|||
Рис. 3.2. Прогнозирование спроса с помощью трендовых моделей |
|
||||||||||
Прогнозирование |
|
|
Стр. 89 из 164 |
J I |
J I x y |
× |
|||||

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.1 II |
|
JJ |
На данном рисунке видны три различных тренда, хотя подписи сделаны для пяти. Это связано с тем, что произошли наложения друг на друга двух пар линий трендов: линия линейного тренда закрыла линию экспоненциального тренда, а линия логарифмического тренда оказалась под степенным трендом. Подтверждением наложения трендов является совпадение значений коэффициентов детерминации.
Графический анализ трендов показывает, что прогнозы по линейному и экспоненциальному трендам будут, скорее всего, завышенными — оптимистическими, а прогнозы по полиномиальному тренду, наоборот — пессимистическими (в перспективе будет падение спроса). Логарифмический и степенной тренды дают промежуточные прогнозы.
Все трендовые модели имеют невысокое качество — их коэффициенты детерминации варьируются от 0,798 (у линейного и экспоненциального трендов) до 0,842 (у полиномиального тренда). Поэтому на практике обычно используют наиболее простые трендовые модели либо выбор типа тренда осуществляется экспертно.
Полиномиальная модель показывает, что рост спроса на продукцию предприятия прекратился и в ближайшее время начнется спад. На наш взгляд естественнее ожидать стабилизацию спроса с незначительным ростом. Поэтому логарифмический и степенной тренды должны давать более ожидаемое значение спроса. Для снижения риска при планировании деятельности от некачественных прогнозов лучше всего рассматривать различные сценарии развития спроса на основе полученных трендов, например, оптимистический, пессимистический и промежуточный (в нашем случае он может рассматриваться как наиболее вероятный).
Прогнозирование |
Стр. 90 из 164 |
|
J I |
|
J I x y × |
|
|

Оглавление 3.3 Оценка и прогнозирование спроса с . . . |
3.3.1 II |
|
JJ |
На основе логарифмического тренда получаем следующие прогнозы. В 11 периоде он составит:
y11 = 2,827 ln(11) + 508,4 = 515,2;
в 12 периоде:
y12 = 2,827 ln(12) + 508,4 = 515,4;
в 13 периоде:
y13 = 2,827 ln(13) + 508,4 = 515,7.
Данные прогнозы оказались несколько ниже, чем средние показатели, полученные в примере 3, но при этом прогнозы по линейной и экспоненциальной моделям близки к прогнозным значениям, рассчитанным методом приростов и с помощью индексов.
Прогнозирование |
Стр. 91 из 164 |
|
J I |
|
J I x y × |
|
|
