
Osnovanija_geometrii_OZO
.pdf
А |
N0 |
|
|
Если прямые пересекаются, то осью симметрии яв- |
|
|
|
|
|
ляется биссектриса любой пары вертикальных уг- |
|
|
|
|
|
||
|
|
N |
|
|
лов, образованных этими прямыми |
|
|
|
|
|
|
M0 |
|
|
b |
|
Пусть a и b не пересекаются. |
|
|
|
Пусть А b, АР а (рис.). Пусть М АР, MN b. |
||
|
|
|
|
||
M |
|
c |
|
|
|
|
|
|
Пусть s = | АР |, х = | АМ |. |
||
|
|
|
|
|
|
Р |
|
|
а |
||
Пусть f (x) – длина перпендикуляра MN – непрерывная функция. Пусть (х) = s – x – непрерывная
Так как f (0) < (0), а f (s) > (s), то х0 (0; s): f (x0) = (х0)
Пусть М0 – точка отрезка АР, соответствующая х0. Так как (х0) = | РМ0 |,
то (М0, а) = (М0, b).
M0N0 b. РМ0N0 – равнобедренный. Проведем с – биссектрису угла РМ0N0 – ось симметрии прямых a и b.
Теорема 5. Если прямая b параллельна прямой a в данном направлении, то прямая а параллельна прямой b в том же направлении.
Доказательство (УИРС)
|
|
|
|
Прямые a и b параллельны по условию. |
|
В |
М' |
|
Пусть В b. По лемме 1 существует ось симметрии |
|
|
b |
с прямых а и b. |
|
|
|
|
||
|
|
d |
|
Пусть А – точка, симметричная В относительно с |
|
|
c |
(А а). Докажем, что всякий луч d с началом А, |
|
|
|
|
||
|
|
|
|
проходящий внутри угла ВАа, пересекает b. |
|
|
d' |
|
Пусть d' – луч, симметричный лучу d относительно |
А |
|
М |
a |
прямой c. Так как b || a, то b || c и а || c, тогда луч d' |
|
|
|
|
пересекает прямую а в некоторой т. М. Тогда луч d |
|
|
|
|
пересекает прямую b в точке М', симметричной М |
|
|
|
|
относительно прямой с. |
Теорема 6. Если прямые а и b параллельны с в данном направлении, то они параллельны между собой в том же направлении.
5.2.3. Расходящиеся прямые
Определение. Две прямые называются расходящимися, если они не пересекаются и не параллельны.
Через каждую точку вне данной прямой проходят две прямые, параллельные ей, и бесконечно много прямых, расходящихся с ней. Все они лежат внутри одной из пар углов, образованных параллельными прямыми.
Теорема 7. Две прямые, перпендикулярные третьей прямой, расходятся Доказательство (УИРС)
Пусть а с, b c. Они не пересекаются (из теорем абсолютной геометрии)
Сдругой стороны, если а || b, то угол параллельности, который прямая а составляет
сперпендикуляром с, был бы равен /2, что противоречит теореме 2 п. 6.2.1.
Теорема 8. Две прямые, которые при пересечении с третьей образуют равные накрест лежащие или соответственные углы, расходятся.
31
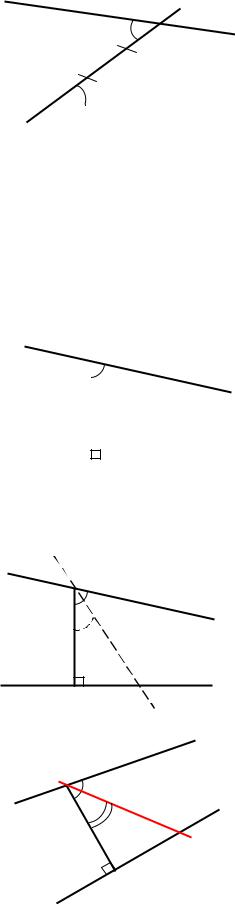
Доказательство |
|
Пусть а и b пересечены с |
|||
|
|
Q |
c |
||
|
|
|
|
b |
О – середина отрезка АВ. ОР а, OQ b. |
|
|
|
|
||
|
|
|
|
||
O |
|
B |
Так как OBQ = OAP (по усл), то OBQ = OAP |
||
|
|
||||
|
|
(из равенства п/уг треугольников). |
|||
|
|
|
|
|
|
A |
|
|
a |
Тогда OP и OQ лежат на одной прямой, к которой а |
|
|
|
||||
|
|
|
|
|
и b перпендикулярны => а и b расходятся |
|
|
P |
|
||
Теорема 9. Всякие две расходящиеся прямые имеют единственный общий перпендикуляр, по обе стороны от которого они неограниченно удаляются одна от другой.
Теорема 10. Две параллельные прямые асимптотически сближаются в сторону параллельности и неограниченно удаляются друг от друга в противоположном направлении
5.2.4. Угол параллельности
Пусть прямые а и b параллельны в некотором направлении и пусть А – произвольная точка прямой b.
|
А |
|
Угол параллельности зависит от выбора точки А на |
|
0 |
b |
прямой b. |
|
|||
|
Не существует двух точек на прямой b, в которых |
||
|
|
|
|
|
|
|
углы параллельности равны (иначе сумма углов |
P |
|
a |
образованного четырехугольника была бы равна |
|
2 , что невозможно). |
||
|
|
|
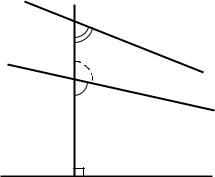
Теорема 1. Угол параллельности в точке А по отношению к прямой а зависит только от расстояния от точки А до прямой а
Доказательство
А |
|
0 |
b |
0' |
|
P |
a |
|
Q |
|
b' |
А'
0'
a'
0'
Q'
P'
Пусть даны прямые а и а' и точки А и A':
(А, а) = (А', a').
Пусть А b, A' b': а || b, a' || b' (для определенности, вправо)
0 и 0' – углы параллельности при точках А и A' по отношению к прямым а и а' Допустим, 0 0', для определенности 0 > 0'.
Отложим справа от луча АР угол, равный углу 0'. Так как по предположению: 0' < 0, то сторона этого угла, отличная от АР, пересекает прямую а в некоторой точке Q. Отложим на прямой a' от точки P' в сторону параллельности прямых a' и b' отрезок
P'Q' = PQ. Тогда APQ = A'P'Q' =>
PAQ = P'A'Q', но тогда от луча A'P' в одну сторону отложены два равных угла, что невозможно
Обозначим (А, а) = s. Так как величина угла параллельности в т.А относительно а определяется только значением s, то она является функцией от s: П(s)
32
В геометрии Лобачевского эта функция играет важную роль. Она называется функ-
цией Лобачевского
Свойства функции Лобачевского
1.П(s) определена на промежутке (0; + )
2.Значения П(s) заключены в промежутке (0; /2)
3.(Теорема 2) Функция Лобачевского является монотонно убывающей функцией Доказательство
А' |
0' |
|
|
b' |
|
|
|
|
А |
|
|
0 |
b |
|
P |
|
a |
Пусть АР – перпендикуляр на а из точки А а.
Пусть А' АР, АР = s, A'P' = s'.
Докажем, что если s' > s, то П(s') < П(s).
Пусть А b || a, A' b' || a в одном направлении, тогда b || b'.
Пусть – угол, смежный с 0
Если 0' + = , то прямые b' и b – расходятся, тем более эта сумма не может быть больше =>
0' + < => 0' < 0
Теорема 3. Функция Лобачевского принимает все значения из промежутка (0; /2).
Следствие. Функция П(s) непрерывна на промежутке (0; + ), при s 0 П(s) /2 и
при s + П(s) 0.
Доказательство
Непрерывность функции П(s) следует из того, что она монотонна и принимает все значения из промежутка (0; /2), предельные соотношения следуют из непрерывности функции П(s).
Замечание. На плоскости Лобачевского возможно расположение трех прямых, не имеющее аналогии на евклидовой плоскости.
Пусть прямые a и b параллельны влево. Они имеют ось симметрии s. На прямой s возьмем произвольную точку А и проведем луч d, параллельный прямой b вправо. Правее точки А на прямой s существует такая точка В, что проведенный в ней перпендикуляр ВС параллелен лучу d. Прямая ВС параллельна прямой b. Так как прямые а и b симметричны прямой s, то прямые ВС и а тоже параллельны. Таким образом, прямые а и b параллельны в одном направлении, прямые b и ВС – в другом, а прямые а и ВС – в третьем.
Фигуру, образованную прямыми а, b и BC называют вырожденным треугольником
или треугольником с бесконечно удаленными вершинами.
5.3. Эквидистанта и орицикл
5.3.1. Эквидистанта
В геометрии Евклида известен факт – ГМТ, равноудаленных от данной прямой а и лежащих по одну сторону от этой прямой, есть прямая.
33
В п.1.4. было показано, что данное утверждение является эквивалентом V постулата, следовательно, на плоскости Лобачевского это утверждение неверно. Определим соответствующее ГМТ на плоскости Лобачевского и рассмотрим его свойства.
Пусть а – некоторая прямая.
Опред. Множество точек, расположенных по одну сторону от прямой а и удаленных от неё на данное расстояние, называется эквидистантой (гиперциклом).
Прямая а – база эквидистанты, перпендикуляр, опущенный из точки эквидистанты на базу (и его длина), называется высотой эквидистанты.
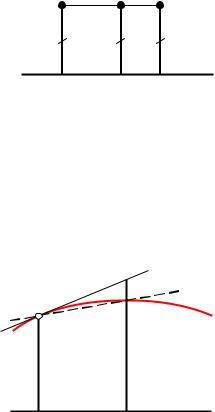
Теорема 1. Никакие три точки эквидистанты не лежат на одной прямой Доказательство Пусть точки А, В, С эквидистанты принадлежат одной прямой.
А |
В С |
Пусть АА1, ВВ1, СС1 – перпендикуляры к а. |
|
|
Четырехугольник А1АСС1 – четырехугольник Сак- |
|
|
кери, имеющий 4 прямых угла, что невозможно на |
аплоскости Лобачевского
А1 В1 С1
Следствие. Любая прямая, лежащая в плоскости эквидистанты, пересекается с эквидистантой не более, чем в двух точках.
Теорема 2. Все точки эквидистанты лежат по одну сторону от прямой t, проведенной через любую точку А эквидистанты перпендикулярно к её высоте АА' (по ту же сторону, что и база а). Эта прямая является касательной к эквидистанте.
Доказательство
t 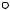 Х
Х
А 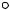 Х1
Х1
A' Х'
1.Так как t АА' и a AA', то t и а – расходятся. Таким образом, все точки прямой t, отличные от А удалены от прямой а на расстояние, большее, чем
AA'.
2.Пусть Х – произвольная точка прямой t, X' – проекция этой точки на а, X1 – пересечение XX' с эквидистантой.
Если Х1 А, то | XX1 | 0, а секущая АХ1 имеет предельное положение – прямую t. Таким образом t – касательная
Теорема 3. Для того, чтобы две эквидистанты были равны, необходимо и достаточно, чтобы они имели равные высоты.
Эквидистанта обладает некоторыми свойствами, общими с прямой и окружностью. Так, прямую можно "двигать по самой себе", то есть если прямую передвинуть так, что какие-либо две её точки А и В совпадут с точками A' и B' той же прямой, то прямая во втором положении совпадет с первоначальной прямой. Аналогично с окружностью, которую можно вращать вокруг её центра, и она будет "скользить сама по себе".
Кривые, обладающие таким свойством, называются кривыми постоянной кривизны. В геометрии Евклида к таким кривым относятся только прямые и окружности. В геометрии Лобачевского этим свойством обладает также эквидистанта. Если основание А1 перпендикуляра АА1 вместе с этим перпендикуляром передвигать по прямой а, то ко-
34

нец А перпендикуляра опишет эквидистанту, при таком движении эквидистанта будет скользить сама по себе, т.е. она имеет постоянную кривизну. Эквидистанты с различной высотой не могут быть совмещены ни одним своим куском, так же как окружности разного радиуса.
Другие свойства эквидистанты:
С эквидистантой связан пучок расходящихся прямых – множество всех прямых, перпендикулярных к базе эквидистанты. Прямые этого пучка называются осями эквидистанты.
1. Эквидистанта симметрична относительно любой своей оси. Доказательство
|
M |
|
|
M1 |
Пусть u – база эквидистанты, а – одна из её осей. |
|||
|
|
|
||||||
|
|
|
Пусть М – произвольная точка эквидистанты , M1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
симметрична точке М относительно прямой а, до- |
|
|
|
|
|
|
|
|
кажем, что М1 . |
|
|
|
|
|
|
|
|
Пусть М' и М'1 – проекции точек М и М1 на прямую |
|
|
|
|
|
|
|
u |
и, тогда М' и М'1 симметричны относительно пря- |
|
|
|
|
|
|
|
мой а, поэтому ММ' = М1М'1. Отсюда и следует, |
|
|
|
|
|
|
|
|
||
|
M' |
|
a |
M1' |
||||
|
|
что М1 . |
||||||
|
|
|||||||
2°. В каждой точке эквидистанты существует касательная, которая перпендикулярна к оси, проведенной через точку касания.
Хордой эквидистанты называется любой отрезок, соединяющий две точки эквидистанты.
3°. Любая прямая, содержащая хорду эквидистанты, является секущей равного наклона к осям, проходящим через концы хорды.
Доказательство Пусть АВ – хорда данной эквидистанты, а АА' и ВВ' – ее оси, где А' и В' – проекции
точек А и В на базу эквидистанты. По определению эквидистанты отрезки АА' и ВВ' равны, поэтому ABB'А' – четырехугольник Саккери: А'АВ = В'ВА.
4°. Серединный перпендикуляр к любой хорде эквидистанты является ее осью.
5.3.2. Орицикл
Теорема 4. Каковы бы ни были параллельные прямые а и b, через всякую точку А прямой а проходит единственная секущая равного наклона к этим прямым.
Доказательство
a |
l |
b |
m |
|
|
A |
|
B |
Существование
Проведем ось симметрии l к прямым a и b. Проведем через А прямую m l
m b = B и (АВ, а) = (АВ, b)
Единственность
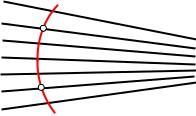
Если сдвигать т.В по прямой b, тогда один из углов между лучом АВ и прямой b увеличивается, а лежащий по
35
|
ту же сторону от прямой АВ угол между лучом АВ и |
|
прямой а уменьшается. |
а А |
Рассмотрим пучок прямых, параллельных в одном на- |
|
правлении. Пусть а – некоторая прямая этого пучка, А |
|
а. На каждой прямой m пучка, отличной от а, сущест- |
|
вует единственная точка М такая, что АМ есть секущая |
|
равного наклона прямых а и m. Множество таких точек |
|
М (включая А) называется орициклом. Прямые данного |
|
пучка называются его осями. |
Орицикл определяется пучком параллельных прямых и некоторой точкой А на одной из них. Пусть В – точка орицикла , рассмотрим орицикл ', определенный тем же пучком и точкой В. Заданные таким образом орициклы совпадают.
Теорема 5. Никакие три точки орицикла не лежат на одной прямой Доказательство
Допустим, что точки А, В, С орицикла лежат на одной прямой, тогда серединные перпендикуляры к отрезкам АВ и ВС параллельны и имеют общий перпендикуляр, что невозможно
Свойства орицикла аналогичны свойствам окружности и эквидистанты, но есть еще одно свойство, которого нет у окружности и эквидистанты.
Теорема 6. Все орициклы равны Доказательство
Пусть орициклы и ' определены соответственно точками А и А' и проходящими через них осями а и а'. Тогда по аксиоме подвижности существует движение, совмещающее точки А и A' и положительные направления осей а и а', значит, и орициклы и'
5.4. Некоторые факты геометрии Лобачевского
1. Каждый угол содержит внутри себя такие точки, через которые нельзя провести прямых, пересекающих обе стороны угла.
Т.е. если прямая, проходящая через такую точку, пересечет одну сторону угла, то она не пересечет другую его сторону.
В самом деле, утверждение, что через любую точку внутри угла всегда можно провести прямую, пересекающую обе стороны угла, является эквивалентом V постулата (Лежандр)
2. Каков бы ни был острый угол, всегда существует такой перпендикуляр к одной стороне этого угла, который не пересекает другую сторону.
3. Каков бы ни был острый угол, всегда существует перпендикуляр к одной его стороне, параллельный другой стороне.
36
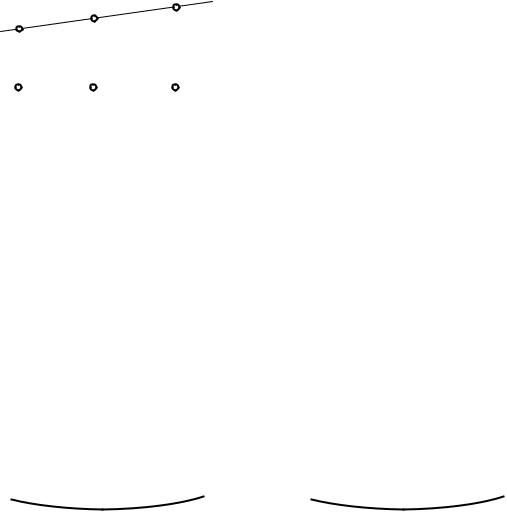
4. В геометрии Лобачевского существуют треугольники, около которых нельзя описать окружность.
Утверждение, что около каждого треугольника можно описать окружность, является эквивалентом V постулата Евклида (Фаркаш Бойяи, см. п.1.4.)
Перпендикуляр к хорде эквидистанты, проведенный через её середину и являющийся ГМТ, равноудаленных от вершин хорды, есть прямая, перпендикулярная к базе этой эквидистанты.
5. Около всякого треугольника, вписанного в эквидистанту, нельзя описать окружность.
Пусть АВС вписан в эквидистанту. AA', BB' а (база эквидистанты) AA'B'B – четырехугольник Саккери,
PQ – его ось симметрии (PQ АВ и а)
|
|
|
|
B' |
Пусть около АВС можно описать окружность. |
||
A' |
|
P |
Центр О этой окружности является точкой пересе- |
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
|
|
чения трех ГМТ: 1) равноудаленных от А и В, 2) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равноудаленных от В и С, 3) равноудаленных от В |
|
|
|
|
|
|
|
и С. |
|
|
|
|
|
|
|
|
A' |
|
Q |
B' а |
|
|||
Однако, эти ГМТ перпендикулярны к базе эквидистанты а, следовательно, расходятся, т.е. не имеют общих точек. Следовательно, около АВС нельзя описать окружность.
Замечание. Треугольники, вписанные в эквидистанты, не исчерпывают всех треугольников, около которых нельзя описать окружность.
6. Все полосы между параллельными прямыми равны между собой, т.е. могут быть наложены друг на друга своими точками.
7. Четырехугольники Саккери с равными верхними основаниями и равными соответственно острыми углами при них конгруэнтны.
Доказательство
Пусть в четырехугольниках Саккери ABDC и A'B'D'C' : CD = C'D' и острые углы при CD и C'D' равны.
Наложим четырехугольник A'B'D'C' на четырехугольник ABDC так, что C'D' совпадет с CD. Тогда прямая C'A' пойдет по CA. D'B' пойдет по DB. Определим расположение точек A' и В'.
C |
D |
C' |
D' |
A" |
|
|
|
В" |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
A' |
|
|
B' |
|||
37

Допустим, что они лежат "выше" точек А и В (в точках A" и B"), тогда АВ || СD и А"В" || CD, т.е. АВ || А"В". С другой стороны, они имеют общие перпендикуляры АС и BD, следовательно, они расходятся, что невозможно.
8. Два треугольника, имеющие равные дефекты и по равной стороне, равновелики.
9. Площади двух треугольников относятся, как их дефекты. Отношение площади треугольника к его дефекту есть величина постоянная, не зависящая от треугольника.
5.5.Модели геометрии Лобачевского
5.5.1.Модель Кэли-Клейна
Кэли (Cayley) Артур (1821–1895),
английский математик
1849-1863 – адвокат,
Рассматривал эту деятельность как "средство заработать деньги, чтобы заниматься математикой". За это время издал приблизительно 250 математических работ С 1863 профессор Кембриджского университета.
Основные работы: теории алгебр, квадратичных форм. Установил связь между теорией инвариантов и проективной геометрией.
Его исследования легли в основу истолкования геометрии Лобачевского Автор работ по теории определителей, дифференциаль-
ных уравнений, эллиптических функций. Занимался также сферической астрономией и астрофизикой.
Издал более 900 работ и примечаний, покрывающих почти каждый аспект современной математики.
Клейн (Klein) Феликс (1849–1925),
немецкий математик, член-корреспондент Германской АН в Берлине
С 1872 – профессор математики в Эрлангене,
с1875 – в Мюнхенской Высшей технической школе,
с– 1880 в Лейпцигском университете.
В 1886 Клейн переехал в Геттинген Основные работы по направлениям: неевклидова геомет-
рия, теория непрерывных групп, теория алгебраических уравнений, решение уравнений 5-й, 6-й и 7-й степеней, теория эллиптических функций, теория атоморфных функций, теория многогранников, интегрирование дифференциальных уравнений, абелевы функции
38
Описание модели
Модель была построена английским математиком Кэли, но он сам не усмотрел связи определённых им метрик с геометрией Лобачевского хотя и был знаком с его работами. Связь результатов Кэли с геометрией Лобачевского была установлена немецким математиком Феликсом Клейном в 1870 г.
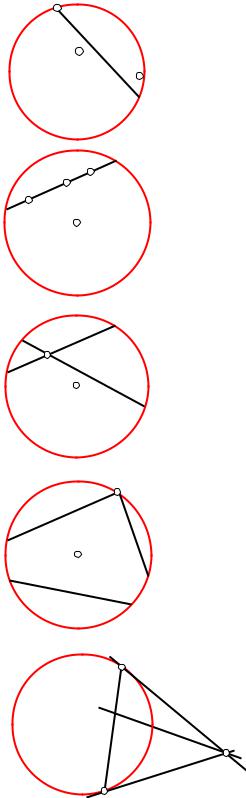
Рассмотрим на евклидовой плоскости некоторую окружность ω с центром О радиуса r = 1, её называют абсолютом.
|
U |
|
Неевклидова точка – любая внутренняя точка абсолюта |
|
ω |
|
|
|
|
Неевклидовая прямая – любая хорда (без концов) окруж- |
|
|
O |
|
|
|
|
ности ω. |
|
|
|
|
|
|
|
V |
Отношения «принадлежность» и «лежать между» пони- |
|
|
маются в обычном смысле. |
|
|
|
|
|
|
|
V |
|
|
B C |
|
Неевклидов отрезок – любой отрезок неевклидовой прямой |
U |
A |
||
|
|
(АВ, АС, ВС, ОВ...) |
|
|
O |
|
|
|
|
|
Неевклидов луч – любая полухорда (AV, BV, CU, OU...) |
|
V |
|
|
|
P A |
Пересекающиеся прямые – любые хорды, пересекающие в |
|
U |
|
||
неевклидовой точке |
|||
O |
|||
|
Неевклидов угол – любой с вершиной в неевклидовой точке |
||
|
Q |
(VAQ, PAV...) |
V
U |
|
Параллельные прямые – любые хорды с общей точкой на аб- |
|
|
солюте (UV || VQ) |
||
|
O |
||
|
Расходящиеся прямые любые хорды, не имеющие общих |
||
M |
Q |
||
точек (UV и MN) |
|||
|
N |
|
V
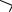 n
n
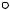 O
O
U
Прямая, перпендикулярная данной изображается пря-
мой, проходящей через внешнюю точку круга по-
Pлюс данной прямой Действительно, так как полюс любого из диаметров –
бесконечно удаленная точка, прямая, перпендикулярная диаметру, проходит через эту точку.
39

Метрические соотношения в модели Кэли-Клейна
Поскольку в модели Клейна плоскости Лобачевского выполняются аксиомы IV группы, можно ввести в ней метрику.
P и Q – две произвольные внутренние точки абсолюта, а UV – хорда абсолюта, проходящая через эти точки, при этом направление отрезка PQ противоположно направлению отрезка UV.
ρ(PQ) = | ln(PQ,UV) |
Функция ρ удовлетворяет аксиомам длины:
10 Функция ρ положительна и определена для всех точек P, Q. Соответствующие пары точек не разделяют друг друга, потому (PQ, UV) > 0. 20 Если точка R лежит между точками P и Q, то ρ(PQ)=ρ(PR)+ρ(RQ).
Из свойств двойного отношения имеем ln (PQ, UV) = ln (PR, UV)·(RQ, UV) = ln (PR,
UV)+ ln (RQ, UV).
30 Если отрезки PQ и P'Q' равны, то ρ(PQ) = ρ(P'Q').
Равенство PQ и P'Q' означает, что существует Л-преобразование, отображающее отрезок PQ, лежащий на хорде UV в отрезок P'Q' хорды U'V'. Тогда по свойству проективного преобразования, (PQ, UV) = (P'Q',U'V'). Из последнего равенства, в силу определения гиперболического расстояния, следует справедливость равенства ρ(PQ)=ρ(P'Q').
40 Существует отрезок AB, такой, что ρ(AB)=1. |
|
|
|
|
|
|
|||
Задачи |
|
|
|
|
|
|
|
||
1. |
Прямые а и b пересекаются. Построить прямую: |
а) параллельную а и расходя- |
|||||||
щуюся |
с |
b; б) параллельную |
а и перпендикулярную |
b; |
в) параллельную |
а |
и |
b; |
|
г) перпендикулярную а и b. |
|
|
|
|
|
|
|
||
2. |
Прямые а и b параллельны. Построить прямую: |
а) параллельную а и расходя- |
|||||||
щуюся |
с |
b; б) параллельную |
а и перпендикулярную |
b; |
в) параллельную |
а |
и |
b; |
|
г) перпендикулярную а и b. |
|
|
|
|
|
|
|
||
3. |
Прямые а и b расходятся. Построить прямую: |
а) параллельную а и расходящуюся |
|||||||
с b; |
б) |
параллельную а и |
перпендикулярную |
b; |
в) |
параллельную |
а |
и |
b; |
г) перпендикулярную а и b.
4.Прямые а и b параллельны, с – расходящаяся с ними обеими. Построить прямую, перпендикулярную с и параллельную а и b.
5.Построить треугольник с "нулевыми" углами.
6.Построить угол параллельности данного отрезка.
7.Построить отрезок, для которого данный угол является углом параллельности.
8.Построить середину отрезка.
9.Построить биссектрису угла.
10.Построить прямые, для которых данный отрезок является их общим перпендикуляром.
11. Найти расстояние между точками А и В: а) А(
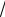 2–1; 0), В(
2–1; 0), В(  2 1;1); б) А(0; 1),
2 1;1); б) А(0; 1),
2 |
2 |
2 |
В(1;1).
2 3
40
