Osnovanija_geometrii_OZO

Теорема (Соотношение между сторонами и углами треугольника). В произвольном треугольнике против большей стороны лежит больший угол.

Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны АС. Докажем, что угол С больше угла В. Для этого отложим на луче АВ отрезок AD, равный сто-

D 2

1

B

Треугольник АСD – равнобедренный. Следовательно, 1 = 2. Угол 1 составляет часть угла С. Поэтому 1 < C. С другой стороны, угол 2 является внешним углом треугольника ВСD. Поэтому 2 > B. Следовательно, имеем C > 1 = 2 > B.

Следствие 1. В произвольном треугольнике против большего угла лежит большая сторона.

Докажем, что если в треугольнике АВС угол С больше угла В, то и сторона АВ больше стороны АС. Действительно, эти стороны не могут быть равны, так как в этом случае треугольник АВС был бы равнобедренным и, следовательно, угол С равнялся бы углу В. Сторона АВ не может быть меньше стороны АС, так как в этом случае, по доказанному, угол С был бы меньше угла В. Остается только, что сторона АВ больше стороны

АС.

Следствие 2. Перпендикуляр, опущенный из данной точки на данную прямую, короче всякой наклонной, проведенной из этой точки к этой прямой.

Следствие 3. Из двух наклонных, проведенных из данной точки к данной прямой, больше та, проекция которой больше.

Действительно, пусть ВС и ВD – наклонные к прямой а, АВ – перпендикуляр и AD > AC. Предположим, что точки С и D лежат по одну сторону от точки А (рис. 5). Тогда угол ВСD тупой как внешний угол острого угла прямоугольного треугольника АВС. Угол BDC острый как угол прямоугольного треугольника АВD. Так как против большего угла треугольника лежит большая сторона, то в треугольнике BDC сторона BD будет больше стороны ВС.

Аналогичным образом рассматривается случай, когда точки С и D лежат по разные стороны от точки А.

3.2. Система аксиом Вейля геометрии Евклида

Вейль (Weyl) Герман (1885-1955), немецкий математик. Работал в различных областях математики. Первые работы посвящены тригонометрическим рядам, рядам по ортогональным функциям и почти периодическим функциям (почти периодические функции Вейля). В теории функций комплексного переменного Вейль впервые дал строгое построение тех разделов этой теории, которые опираются на понятие "риманова поверхность" (теоремы и область Вейля). В математическом анализе Вейль занимался дифференциальными и интегральными уравнениями, в частности создал спектральную теорию дифференциальных операторов. Введенные Вейлем в теории чисел суммы Вейля имели

21

большое значение для аддитивной теории чисел. Наиболее значителен комплекс работ Вейля по теории непрерывных групп и их представлений с применениями к проблемам геометрии и физики. Введенное им понятие пространства аффинной связности играет существенную роль в современной дифференциальной геометрии. Труды Вейля по прикладной линейной алгебре имели значение для последующего создания математического программирования, а работы в области математической логики и оснований математики до сих пор вызывают интерес.

3.2.1. Структура с.а. Вейля

Основные объекты: точка, вектор

Совокупности всех точек и векторов обозначаются соответственно Т и V. Основные отношения: сложение векторов, умножение вектора на число, скалярное

умножение векторов, откладывание вектора от точки. Структура аксиоматики: 5 групп:

I: Аксиомы сложения векторов (4)

II: Аксиомы умножения вектора на действительное число (4) III: Аксиомы размерности (2)

IV: Аксиомы скалярного произведения векторов (3) V: Аксиомы откладывания векторов (2)

I. Аксиомы сложения векторов

Описывает отображение 1: V V V, называемое операцией сложения векторов, которое ставит в соответствие любым двум векторам x и y третий вектор 1(x, y), называемый суммой векторов x и y и обозначаемый x + y.

I1: Коммутативность: для любых двух векторов x и y справедливо равенство x + y = y + x.

I2: Ассоциативность: для любых трех векторов x, y, z справедливо: (x + y) + z = x + ( y + z ).

I3: Существует такой вектор , что для любого вектора x:

x + = + x = x.

I4: Для любого вектора x существует такой вектор x , что x + x = x + x = .

Опред. Вектор называется нулевым, а x – вектором, противоположным вектору x.

II. Аксиомы умножения вектора на действительное число

Вторая группа аксиом описывает отображение 2: V R V, называемое операци-

ей умножения вектора на действительное число. Каждому вектору x и числу R од-

нозначно сопоставляется вектор 2( , x), называемый произведением вектора x на числои обозначаемый x.

2 удовлетворяет следующим аксиомам:

II1: Дистрибутивность относительно сложения векторов:

(x + y) = x + y

22

II2: Дистрибутивность относительно сложения чисел: ( + ) x = x + x

II3: Ассоциативность:

( x) = ( ) x

II4: Умножение на единицу:

1 · x = x

Опред. Векторным пространством над полем действительных чисел R называется множество V, для элементов которого определены операции сложения векторов ( 1(x, y) = x + y) и умножения вектора на действительное число ( 2( , x) = x) так, что выполняются требования аксиом I–II.

Опред. Вектор 1 x1 + 2 x2 + ... + n xn , где 1, 2, ..., n R, называется линейной комбинацией векторов x1, x2 , ..., xn .

Опред. Система векторов x1, x2 , ..., xn называется линейно независимой, если их ли-

нейная комбинация равна в том и только том случае, когда 1 = 2 = ... = n = 0.

III. Аксиомы размерности

III1: Существуют три линейно независимых вектора e1, e2 , e3. III2: Любые четыре вектора линейно зависимы.

Аксиомы I–III позволяют ввести понятие трехмерного векторного пространства: векторное пространство V называется трехмерным векторным пространством V3 над полем R, если выполняются аксиомы группы III.

Аксиоматика n-мерного векторного пространства над полем R: III1': Существует n линейно независимых

III2': Всякая система, содержащая n + 1 вектор, линейно зависима.

Любая система n линейно независимых векторов пространства Vn называется бази-

сом.

IV. Аксиомы скалярного произведения векторов

Описывает отображение 3: V3 V3 R, называемое операцией скалярного умножения векторов, позволяющая любым двум векторам x и y однозначно отнести дейст-

вительное число 3(x, y). Обозначение: x y.

IV1: Коммутативность. Для любых двух векторов x и y: x y = y x

IV2: Линейность. Для любых трех векторов x, y, z и действительных чисел , выполняется равенство

x ( y + z ) = x y + x z . IV3: Для любого вектора x:

x x > 0, если x ; x x = 0, если x = .

Опред. Векторное пространство V3, в котором определена операция скалярного умножения векторов так, что выполняются аксиомы IV, называется евклидовым векторным пространством.

23

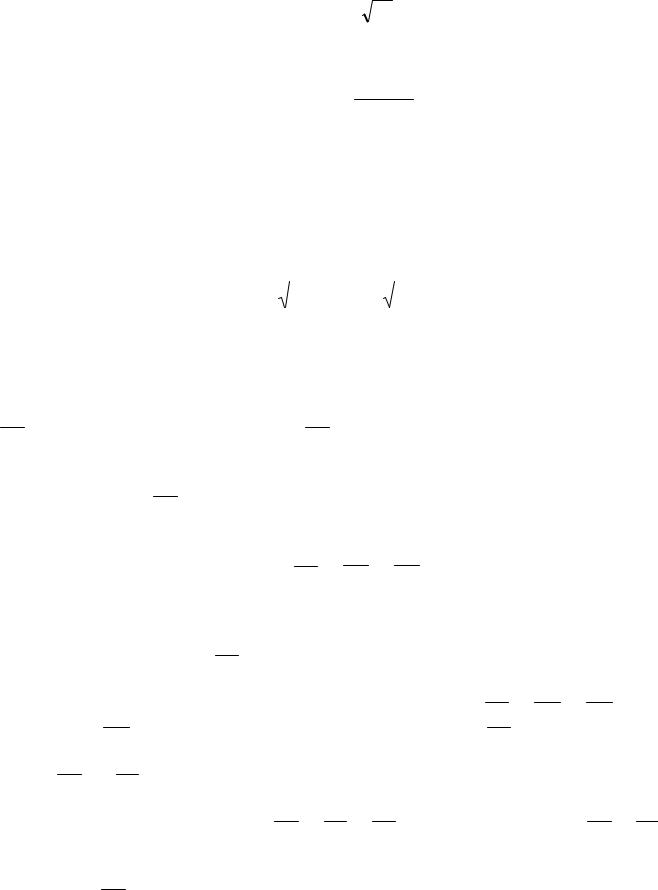
Евклидово векторное пространство является структурой (V, 1, 2, 3) с базисным множеством V и операциями 1, 2, 3.

В ОНР:

xy = x1y1 + x2y2 + x3y3,

x2 = x12 + x22 + x32

где x1, x2, x3 – координаты вектора x, y1, y2, y3 – координаты вектора y в данном базисе.

V. Аксиомы откладывания векторов

Операция откладывания векторов 4: Т Т V, сопоставляющая двум упорядоченным точкам А, В Т, вектор 4(А, В) из векторного пространства V, обозначаемый AB, где А – начальная точка вектора AB, а В – конечная, определяется следующими условиями:

V1: Для каждой фиксированной точки А Т отображение Т V, определенное по закону 4(А, В) = AB, является взаимно однозначным отображением множества точек В Т на множестве векторов из V.

V2: Для любых трех точек А, В, С справедливо равенство:

AB + BC = AC

(аксиома треугольника)

3.2.2. Простейшие следствия из аксиом I–V

1. Любой из векторов AA (А Т) является нулевым вектором пространства V. Доказательство

V2: Для любых точек А, Х Т справедливо равенство: AA + AX = AX . Так как AX V может быть любым вектором, то по I3 AA = .

2. AB = –BA

Доказательство

V2: полагая С = А, получим: AB + BA = AA = , т.е. из I4 векторы AB и BA – противоположные.

3. Если AB = , то точки А, В совпадают. Доказательство

24

V2: ( AB + BC = AC). Так как AB = , то BC = AC, откуда CB = CA и по V1 точки А и В совпадают.

3.2.3. Непротиворечивость системы аксиом Вейля

Для доказательства построим арифметическую модель системы аксиом I–V.

Пусть точка или вектор – любой упорядоченный набор трех действительных чисел х1, х2, х3. Точки: (х1, х2, х3), векторы {х1, х2, х3}.

Числа х1, х2, х3 – координаты точки (вектора).

Сложение векторов: {х1, х2, х3} + {y1, y2, y3} = {x1 + y1; x2 + y2, x3 + y3}.

Легко доказать, что требования аксиом первой группы при этом будут удовлетворе-

ны.

Умножение действительного числа на вектор ( на x{х1, х2, х3}) понимается, как обычное умножение числа на каждое из чисел х1, х2, х3:

x = { x1, x2, x3}

Определенная таким образом операция удовлетворяет аксиомам второй группы. Аксиомы третьей группы также выполняются: векторы

{1, 0, 0}, {0, 1, 0}, {0, 0, 1}

линейно независимы и образуют базис пространства, т.е. любой вектор {х1, х2, х3} является их линейной комбинацией.

Скалярным произведением векторов x{х1, х2, х3} и y{y1, y2, y3} называется величи-

точка В определяется упорядоченным набором чисел:

b1 = a1 + x1, b2 = a2 + x2, b3 = a3 + x3.

Справедливость V2 ( AB + BC = AC).

Пусть А(а1, а2, а3), B(b1, b2, b3), С(с1, с2, с3). Тогда

AB = {b1 – a1, b2 – a2, b3 – a3}, BC = {c1 – b1, c2 – b2, c3 – b3}, AC{c1 – a1, c2 – a1, c3 – a3}

Подставив, получим, AB + BC = {c1 – a1, c2 – a1, c3 – a3} = AC.

Таким образом, приходим к выводу: система аксиом Вейля евклидовой геометрии непротиворечива, если непротиворечива арифметика действительных чисел.

§4. Некоторые факты абсолютной геометрии

Факты абсолютной геометрии основаны на аксиомах I–IV групп.

Все теоремы, которые были введены при изучении аксиоматики Гильберта (до V группы), являются теоремами абсолютной геометрии. Рассмотрим также те, которые необходимы для построение геометрии Лобачевского.

4.1. Сумма углов и дефект треугольника

АВС, Т – обозначение треугольников, (АВС), (Т) – обозначение суммы углов треугольника

25

Отрезок ВС называется его нижним основанием, AD – верхним основанием. Стороны АВ и СD – боковые.

В случае евклидовой геометрии такой четырехугольник будет прямоугольником.

Теорема. Четырехугольник Саккери имеет ось симметрии, проходящую через середины оснований; эта ось является общим перпендикуляром к основаниям. Углы при верхнем основании четырехугольника Саккери равны и не превосходят /2.

Теорема. Пусть в четырехугольнике углы при нижнем основании прямых, а боковые стороны не равны. Тогда из двух углов при верхнем основании больше тот, который лежит против большей стороны. Справедливо и обратное утверждение.

§5. Геометрия Лобачевского

Лобачевский Николай Иванович (1792 – 1856)

Почти всю жизнь Лобачевский прожил в Казани, окончил там гимназию, затем Казанский университет. Много лет был ректором Казанского университета, внёс очень большой вклад в его развитие. При этом Лобачевский вёл не только научнопедагогическую деятельность. Благодаря его действиям университет удалось спасти дважды: во время эпидемии холеры в 1830 г, от пожара, уничтожившего большУю часть Казани в 1842 году.

Основные достижения Лобачевского:

–первым сумел снять проблему V постулата

–c 1826 года работа над проблемами новой ("воображаемой") геометрии, впервые представленная на заседании отделения физико-математических наук Казанского университета.

Эта работа в то время не была понята и не получила поддержки.

В России при жизни Лобачевского публично оценил его открытие только профессор П.И.Котельников (1842). Европейские ученые узнали о работах Лобачевского лишь в 1840, и в 1842 по представлению К.Гаусса он был избран членом-корреспондентом Гёттингенского научного общества.

–ряд работ по математическому анализу

–общее определение функциональной зависимости, позже введенное в науку Ди-

рихле

–в алгебре: метод приближенного решения уравнений любой степени.

Работы:

–О началах геометрии (1829–1830),

–Воображаемая геометрия (1835),

–Применение воображаемой геометрии к некоторым интегралам (1836), Новые начала геометрии с полной теорией параллельных (1835–1838),

–Геометрические исследования по теории параллельных линий (1840).

Николай Иванович Лобачевский умер непризнанным.

5.1. Система аксиом Лобачевского

Планиметрия Лобачевского строится на основе 5 групп аксиом, из которых первые четыре – аксиомы абсолютной геометрии, аксиома V группы – отрицание аксиомы параллельности Евклида: VЛ

27

VЛ: Существуют такая прямая а и такая не лежащая на ней точка А, что через точку А проходит не менее двух прямых, не пересекающих а.

Теорема 1. Сумма углов всякого треугольника меньше (дефект больше нуля). Сумма углов всякого четырехугольника меньше 2 . В любом четырехугольнике Саккери угол при верхнем основании острый.

Следует из Vл и теорем абсолютной геометрии

Следствие. На плоскости Лобачевского нет прямоугольников

Теорема 2. Каковы бы ни были прямая а и не лежащая на ней точка А, через точку А проходит не менее двух прямых, не пересекающих прямую а.

Доказательство (УИРС)

Аналогично, ВВ2 образует с b и с равные накрест лежащие углы => (ВВ1В2) = – противоречие теореме 1. 

На плоскости Лобачевского выполняются все теоремы абсолютной геометрии, в частности признаки равенства треугольников. Рассмотрим еще один признак равенства треугольников, не имеющий места в геометрии Евклида

Теорема 3. Если у треугольников АВС и А'B'C' равны соответствующие углы А и А', B и В', С и С', то эти треугольники равны.

Доказательство (УИРС)

Возьмем треугольник А1В1С1, равный треугольнику АВС так, что А1 совпадает с А', С1 лежит на луче А'C', а вершина В1 лежит в той же полуплоскости с границей А'C', в которой расположена точка B'. Так как А = A', то В1 лежит на луче A'B'.

Докажем, что вершины B' и В1, C' и С1 совпадают. Допустим, это не так. Возможны два случая

28

Так как в треугольниках А1В1С1 и А'B'C' равны углы В1 и B', С1 и С', то(B1C1С'B') = B' + C' + ( – C1) + ( – B1) = 2 , что невозможно по теореме 1. 

5.2. Параллельные и расходящиеся прямые

На евклидовой плоскости непересекающиеся прямые называются параллельными. Параллельность прямых на евклидовой плоскости можно характеризовать и другими свойствами, например, наличием у них многих общих перпендикуляров или постоянством длин этих перпендикуляров.

На плоскости Лобачевского для двух непересекающихся прямых эти утверждения неверны. Здесь возможны два случая: прямые имеют общий перпендикуляр и прямые не имеют общего перпендикуляра.

5.2.1. Определение параллельных прямых

Теорема 1. Каковы бы ни были прямая а и не лежащая на ней точка А, существует бесконечно много прямых, проходящих через точку А и не пересекающих прямую а.

Доказательство

МА.

b" B A D

В силу того, что точек на отрезке бесконечно много, следует справедливость теоремы. 

b1 дикуляр к а. Проведем через А прямую b, не пересе-

Теорема 2. Справедливо неравенство: 0 < 0 < /2.

Пусть Х – некоторая точка прямой а (рис.). Обозначим через острый угол между лучами АР и АХ.

29

Для любой прямой b1, проходящей через точку А и не пересекающей прямую а, выполняется неравенство > , где – угол, определенный выше. Поэтому:

0 = inf > 0.

Проведем через точку А прямую b, перпендикулярную прямой АР. Она не пересекает прямую а. Так как по теореме 2 (6.1.) через точку А можно провести еще одну прямую

b', не пересекающую прямую а, то эта прямая составляет с перпендикуляром острый угол 1. Отсюда: 0 = inf 1 < /2. 

Теорема 3. Пусть А а, АР – перпендикуляр, опущенный на а. Через точку А проведем прямые b1 и b2, составляющие с лучом АР справа и слева углы, равные 0. Тогда прямые b1 и b2 не пересекают прямую а.

Доказательство (УИРС)

Пусть прямая b1 пересекает прямую а в некоторой точке С. На луче РС возьмем точку D, лежащую дальше от точки Р, чем точка С. Пусть PAD = . Тогда 0 < . С другой стороны, для всех углов выполняется: > , откуда 0 , что невозможно. 

Определение. Граничные прямые пучка прямых, проходящих через точку А и не пересекающих а, называются параллельными прямой а. Одна из них параллельна прямой а

вправо, другая – влево.

Через каждую точку, не лежащую на данной прямой, проходят две параллельные ей прямые. По теореме 4 – если прямая b параллельна прямой а вправо (влево) в некоторой точке, то она параллельна прямой а вправо (влево) во всякой своей точке.

5.2.2. Свойства параллельных прямых

Лемма 1. Для любых двух прямых существует ось симметрии Доказательство

30