
ИДЗ Математика ИКРиМ 1 семестр v2
.docМинистерство образования и науки
ФГБОУ ВПО Уральский государственный педагогический университет
Математический факультет
Кафедра высшей математики
В.Ю. Бодряков
Индивидуальные домашние задания
по дисциплине «Математика»
Екатеринбург – 2012
Составители: В.Ю. Бодряков
Индивидуальные домашние задания по дисциплине «Математика». Екатеринбург: УрГПУ, 2012, с.
Индивидуальные домашние задания (ИДЗ) по дисциплине «Математика» предназначены для студентов очной и заочной форм обучения нематематических факультетов УрГПУ, изучающих курс математики в соответствии с требованиями Федеральных государственных образовательных стандартов (ФГОС) по соответствующим направлениям подготовки. Работа содержит 12 индивидуальных домашних заданий (ИДЗ) по 30 вариантов в каждом, содержащих различные задания по дисциплине «Математика».
Целью настоящего комплекта ИДЗ является ознакомление студентов с основами линейной алгебры и началами математического анализа. При решении заданий по линейной алгебре учащиеся отработают навыки действий с определителями и матрицами, а также решения систем неоднородных и однородных линейных алгебраических уравнений. При решении заданий по математическому анализу студенты освоят технику вычисления пределов функции, получат навыки исследования функций одной переменной с применением аппарата дифференциального исчисления. Структурно комплект ИДЗ может быть разбит на три блока: ИДЗ-1-4 – алгебраический блок; ИДЗ-5-8 – основы теории пределов и дифференциального анализа; ИДЗ-9-12 – прикладные аспекты применения дифференциального анализа для исследования функции одной переменной. В зависимости от степени подготовки студентов и объема учебных часов, выделенных на изучение дисциплины, преподаватель может варьировать объем выполняемых ИДЗ.
В целом, самостоятельное решение индивидуальных заданий позволяет углубить теоретические знания, отработать практические навыки решения задач по дисциплине. Во введении к работе приведены примеры решения типовых заданий по теме с необходимыми методическими указаниями.
Рецензент:
© Уральский государственный педагогический университет, 2012
ИДЗ-1. Действия с определителями.
ИДЗ-2. Действия с матрицами.
ИДЗ-3. Решение неоднородной системы линейных алгебраических уравнений.
ИДЗ-4. Решение однородной системы линейных алгебраических уравнений.
ИДЗ-5. Вычисление пределов с использованием теорем о пределах.
ИДЗ-6. Вычисление пределов с использованием замечательных пределов.
ИДЗ-7. Исследование функции на непрерывность.
ИДЗ-8. Дифференцирование функций.
ИДЗ-9. Вычисление производных.
ИДЗ-10. Правило Лопиталя.
ИДЗ-11. Полное исследование функции и построение ее графика.
ИДЗ-12. Решение задачи оптимизации.
Решение «нулевого варианта ИДЗ по Математике
ИДЗ-1. Действия с определителями
Для данного определителя :
= 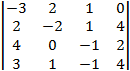 .
.
а) найти алгебраические дополнения элементов 1-ой строки и 1-го столбца; б) вычислить определитель , приведя его к треугольному виду, или получив предварительно нули в к.-л. строке или столбце; в) проверить расчет, применяя разложение определителя по элементам 1-ой строки или 1-го столбца и используя алгебраические дополнения соответствующих элементов из задания а).
Решение: а) Как известно, алгебраическим дополнением Aij элемента aij данного определителя называется определитель порядка на единицу меньшего, полученный из исходного путем вычеркивания i-ой строки и j-ого столбца; при этом знак алгебраического дополнения определяется как (–1)i+j. В данной задаче,
A11 = (–1)1+1 =
= 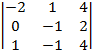 =
= 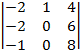 = –
= –![]() = –(–28 – (–1)6)
= 10;
= –(–28 – (–1)6)
= 10;
A12 = (–1)1+2 = –
= –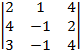 = –
= –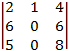 =
= ![]() = 68 – 56
= 18;
= 68 – 56
= 18;
A13 = (–1)1+3 =
= 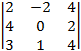 =
= 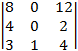 = –
= –![]() = –(82 – 412)
= 32;
= –(82 – 412)
= 32;
A14 = (–1)1+4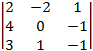 = –
= –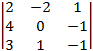 = –
= –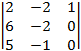 = –
= –![]() =
= ![]() = 6 – 10 = –4;
= 6 – 10 = –4;
A21 = (–1)2+1 = –
= – = –
= –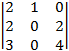 =
= ![]() = 24 – 32
= 2;
= 24 – 32
= 2;
A31 = (–1)3+1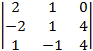 =
= 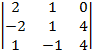 =
= 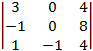 =
= ![]() = 38 + 14
= 28;
= 38 + 14
= 28;
A41 = (–1)4+1 = –
= –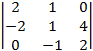 = –
= – = –2
= –2![]() = –2(22
+ 14) = –16.
= –2(22
+ 14) = –16.
б) Вычислить определитель , приведя его к треугольному виду, или получив предварительно нули в к.-л. строке или столбце:
=  =
=  = 1
= 1 =
= 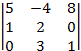 =
=
= 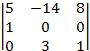 = (–1)
= (–1)![]() = 2
= 2![]() = 2(71
+ 34) = 38.
= 2(71
+ 34) = 38.
в) проверим расчет, применяя разложение определителя по элементам 1-ой строки и (или) 1-го столбца и используя алгебраические дополнения соответствующих элементов из задания а).
Разложение по первой строке:
= a11A11 + a12A12 + a13A13 + a14A14 = (–3)10 + 218 + 132 + 0(–4) = –30 + 36 + 32 = 38.
Разложение по первому столбцу:
= a11A11 + a21A21 + a31A31 + a41A41 = (–3)10 + 22 + 428 + 3(–16) = –30 + 4 + 112 – 48 = 38.
Ответ: а) Алгебраические дополнения: A11 = 10; A12 = 18; A13 = 28; A14 = –4; A21 = 2; A31 = 28; A41 = –16; б), в) величина определителя = 38.
ИДЗ-2. Действия с матрицами
Даны две матрицы A и B:
A = 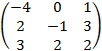 ; B
=
; B
= 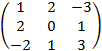 .
.
Найти: а) AB; б) BA; в) A–1; г) AA–1; д) A–1A.
Решение: а) AB
= 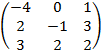
 =
=
= 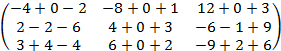 =
= 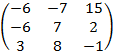 .
.
б) BA = 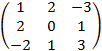
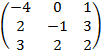 =
=
= 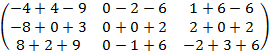 =
=  .
.
Можно заметить, что AB BA, т.е. в общем случае операция умножения матриц неперестановочна.
в) Вычислим обратную матрицу A–1. Как известно, обратная матрица к данной матрице A может быть найдена по формуле:
A–1
= ![]()
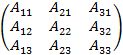 ,
,
где =  – определитель матрицы A;
A* =
– определитель матрицы A;
A* =  – транспонированная матрица алгебраических
дополнений к элементам aij
исходной матрицы A
(присоединенная матрица). Обратная
матрица A–1
существует при
0.
– транспонированная матрица алгебраических
дополнений к элементам aij
исходной матрицы A
(присоединенная матрица). Обратная
матрица A–1
существует при
0.
Определитель данной матрицы A равен:
= 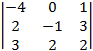 =
=  = 1
= 1![]() = 142 – 11(–1)
= 39 0.
= 142 – 11(–1)
= 39 0.
Вычислим алгебраические дополнения к элементам матрицы A:
A11 = (–1)1+1![]() = (–1)2 – 23
= –8;
= (–1)2 – 23
= –8;
A12 = (–1)1+2![]() = –(22 – 33)
= 5;
= –(22 – 33)
= 5;
A13 = (–1)1+3![]() = 22 – 3(–1)
= 7;
= 22 – 3(–1)
= 7;
A21 = (–1)2+1![]() = –(02 – 12)
= 2;
= –(02 – 12)
= 2;
A22 = (–1)2+2![]() = (–4)2 – 31
= –11;
= (–4)2 – 31
= –11;
A23 = (–1)2+3![]() = –((–4)2 – 30)
= 8;
= –((–4)2 – 30)
= 8;
A31 = (–1)3+1![]() = 03 – (–1)1
= 1;
= 03 – (–1)1
= 1;
A32 = (–1)3+2![]() = –((–4)3 – 21)
= 14;
= –((–4)3 – 21)
= 14;
A33 = (–1)3+3![]() = (–4)(–1) – 20
= 4;
= (–4)(–1) – 20
= 4;
Таким образом, матрица алгебраических
дополнений матрицы A
есть  ;
транспонированная к ней матрица
(присоединенная матрица) A*
=
;
транспонированная к ней матрица
(присоединенная матрица) A*
=  .
Наконец, обратная матрица матрицы A
равна:
.
Наконец, обратная матрица матрицы A
равна:
A–1 = ![]()
 .
.
г) Удостоверимся в правильности расчетов, вычислив произведение AA–1:
AA–1 = 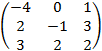
![]()
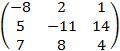 =
= ![]()

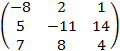 =
=
= ![]()
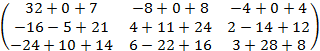 =
= ![]()
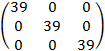 =
= 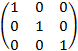 .
.
д) Удостоверимся в правильности расчетов, вычислив произведение A–1A:
A–1A
= ![]()

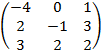 =
=
= ![]()
 =
= ![]()
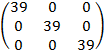 =
=  .
.
Как видно, AA–1 = A–1A = E, где E – единичная матрица. Это значит, что матрица A–1 вычислена правильно.
Ответ: а) AB = 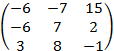 ;
б) BA =
;
б) BA =  ;
;
в) A–1
= ![]()
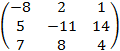 ;
г), д) AA–1
= A–1A
= E.
;
г), д) AA–1
= A–1A
= E.
ИДЗ-3. Решение неоднородной системы линейных алгебраических уравнений
Проверить совместность системы уравнений и в случае совместности решить ее: а) по правилам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса:
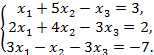
Решение: Совместность данной системы линейных неоднородных алгебраических уравнений проверим по теореме Кронекера – Капелли, утверждающей, что система совместна тогда и только тогда, когда ранги основной (rA) и расширенной (rB) матриц системы равны: rA = rB = r. При этом, если r = n, где n – порядок системы, система имеет единственное решение.
Рангом матрицы называется наиболее высокий порядок определителя, составленного из ее элементов, отличный от нуля.
В данном случае, определитель основной матрицы A системы уравнений:
= 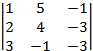 =
= 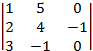 = –(–1)
= –(–1)![]() = 1(–1) – 35
= –16 0,
= 1(–1) – 35
= –16 0,
т.е. rA = 3 = n. Установим значения определителей, составленных из элементов расширенной матрицы, заменяя последовательно столбцом свободных членов 1-ый, 2-ой и 3-ий столбцы основной матрицы системы:
detB1
= 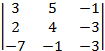 =
= 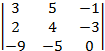 =
= 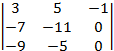 = (–1)
= (–1)![]() =
=
= –(35–99) = 64 0;
detB2
= 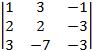 =
= 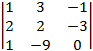 =
=  = (–1)
= (–1)![]() = –(9 + 7) =
= –(9 + 7) =
= –16 0;
detB3
= 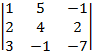 =
=  =
=  = (–2)
= (–2)![]() = –2(–10
– 6) =
= –2(–10
– 6) =
= 32 0.
т.е. rB = 3 = rA. Т.о., ранги основной и расширенной матриц системы совпадают и равны числу переменных n = 3, т.е. система однозначно разрешима.
а) Для нахождения решения системы применим правила Крамера, используя значения вычисленных выше определителей:
x1
= ![]() detB1
= –
detB1
= – ![]() 64
= –4;
64
= –4;
x2
= ![]() detB2
= –
detB2
= – ![]() (–16)
= 1;
(–16)
= 1;
x3
= ![]() detB3
= –
detB3
= – ![]() 32
= –2.
32
= –2.
Окончательно, решение системы есть ![]() =
= ![]() .
.
б) Для нахождения решения системы с помощью обратной матрицы запишем систему уравнений в матричной форме:
A![]() =
= ![]() ,
,
где A =  – матрица системы;
– матрица системы; ![]() и
и ![]() =
= ![]() – столбец переменных и свободных
членов, соответственно. Тогда решение
системы в матричном виде есть:
– столбец переменных и свободных
членов, соответственно. Тогда решение
системы в матричном виде есть:
![]() = A–1
= A–1![]() .
.
Остается найти обратную матрицу A–1 системы. Для этого вычислим матрицу дополнений и транспонируем ее, т.е. вычислим присоединенную матрицу A* к матрице A.
A11 = (–1)1+1![]() = 4(–3)
– 13 = –15;
= 4(–3)
– 13 = –15;
A12 = (–1)1+2![]() = –(2(–3)
+ 33) = –3;
= –(2(–3)
+ 33) = –3;
A13 = (–1)1+3![]() = 2(–1)
– 34 = –14;
= 2(–1)
– 34 = –14;
A21 = (–1)2+1![]() = –(5(–3)
– 11) = 16;
= –(5(–3)
– 11) = 16;
A22 = (–1)2+2![]() = –(1(–3)
– 3(–1)) = 0;
= –(1(–3)
– 3(–1)) = 0;
A23 = (–1)2+3![]() = –(1(–1)
– 35) = 16;
= –(1(–1)
– 35) = 16;
A31 = (–1)3+1![]() = 5(–3)
– 4(–1) = –11;
= 5(–3)
– 4(–1) = –11;
A32 = (–1)3+2![]() = –(1(–3)
– 2(–1)) = 1;
= –(1(–3)
– 2(–1)) = 1;
A33 = (–1)3+3![]() = 14 –
25 = –6.
= 14 –
25 = –6.
Теперь присоединенной матрицей будет
матрица A* =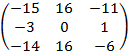 ,
а обратной матрицей – матрица A–1
=
,
а обратной матрицей – матрица A–1
= ![]()
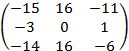 .
.
Решением системы будет
![]() = A–1
= A–1![]() =
= ![]()
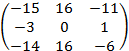
![]() = –
= – 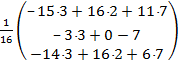
=
=
= – ![]()
![]() =
= ![]() .
.
в) Решим данную систему методом Гаусса (методом исключения):

Исключим x1 из второго и третьего уравнений. Для этого первое уравнение умножим на 2 и вычтем из второго уравнения; первое уравнение умножим на 3 и вычтем из третьего уравнения. Получим
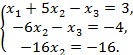
Последовательно находим x2 = 1; x3 = 4 – 61 = –2; x1 = 3 – 51 –2 = –4.
Ответ: Решение системы: ![]() =
= ![]() .
.
ИДЗ-4. Решение однородной системы линейных алгебраических уравнений
Решить однородную систему линейных алгебраических уравнений:
а) 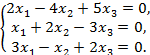 б)
б)
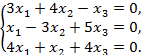
Решение: а) Вычислим определитель системы:
= 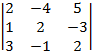 =
=  =
= 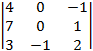 = –(–1)
= –(–1)![]() = 4 + 7 = 11 0.
= 4 + 7 = 11 0.
Т.к. определитель однородной системы линейных уравнений отличен от нуля, то система имеет единственное нулевое (тривиальное) решение x1 = x2 = x3 = 0.
б) Вычислим определитель системы:
= 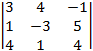 =
=  =
=  = 0.
= 0.
Т.к. определитель однородной системы линейных уравнений равен нулю, то система имеет бесчисленное множество решений. Нетрудно убедиться, что ранг матрицы данной системы уравнений размерности n = 3 равен rA = 2. Иными словами, в данной системе уравнений независимыми являются только два уравнения из трех; используем, например, первое и второе уравнения:
![]()
Так как определитель 2
= ![]() = –9 – 4 = –13 из коэффициентов при
неизвестных x1
и x2 не равен
нулю, то в качестве базисных неизвестных
можно взять x1
и x2. С учетом
сказанного, систему можно переписать
в виде:
= –9 – 4 = –13 из коэффициентов при
неизвестных x1
и x2 не равен
нулю, то в качестве базисных неизвестных
можно взять x1
и x2. С учетом
сказанного, систему можно переписать
в виде:
![]()
Решение этой системы получим с помощью формул Крамера:
x1 = ![]()
![]() =
= ![]() = –
= – ![]() x3;
x3;
x2 = ![]()
![]() =
= ![]() =
= ![]() x3.
x3.
Таким образом, нетривиальным решением
системы является тройка действительных
чисел x1 = – ![]() x3, x2
=
x3, x2
= ![]() x3, x3
R.
x3, x3
R.
Ответ: а) x1
= x2 = x3
= 0; б) x1 = – ![]() x3, x2
=
x3, x2
= ![]() x3, x3
R.
x3, x3
R.
ИДЗ-5. Вычисление пределов с использованием теорем о пределах
Вычислить пределы, применяя теоремы о пределах:
а) ![]() ; б)
; б)
![]() ; в)
; в)![]() .
.
Решение: а) При x –2 числитель и знаменатель, как нетрудно убедиться, обращаются в нуль, давая под пределом неопределенность вида {0/0}. Поэтому в данном случае непосредственное применение теоремы о пределе отношения невозможно. Предварительно преобразуем дробь для избавления от неопределенности:
5x2 + 13x + 6 = (5x + 3)(x + 2); 3x2 + 2x – 8 = (3x – 4)(x + 2).
После простых преобразований возможно применение теорем о пределах:
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
