ИДЗ Математика ИКРиМ 1 семестр v2

б) При n   числитель и знаменатель обращаются в бесконечность, давая под пределом неопределенность вида {/}. Поэтому и здесь непосредственное применение теоремы о пределе отношения невозможно. Как и выше, необходимо предварительное преобразование дроби для избавления от неопределенности, для чего разделим и числитель и знаменатель на старшую степень выражения, в данном случае n⁴:

= = = .

в) При x  4 числитель и знаменатель обращаются в нуль, давая под пределом неопределенность вида {0/0}. Поэтому непосредственное применение теоремы о пределе отношения невозможно. Необходимо предварительное преобразование дроби для избавления от неопределенности. Для этого числитель и знаменатель домножим на сопряженную сумму и разложим разность кубов в знаменателе на множители:

=  = = =

= = .

Полученное выражение уже не имеет особенности при x  4 и после простых преобразований возможно применение теорем о пределах:

= = = = .

Ответ: а) = ; б) = ; в) = .

ИДЗ-6. Вычисление пределов с использованием замечательных пределов

Вычислить пределы, применяя I и II замечательные пределы:

а) ; б) .

Решение: Выражения для I и II замечательного пределов есть, соответственно:

= 1;

= e.

а) Путем несложных преобразований приведем данный предел к стандартному виду II замечательного предела:

= = =.

Для удобства выполним замену переменной под знаком предела. Обозначим x – 1 = t. Тогда при x   и новая переменная t  . Кроме того, x = (t + 1) и 2 – 5x = 2 – 5(t + 1) = 2 – – t = – – t. Продолжим выкладки:

= =

=  = 1 = .

б) Приведем данный предел к стандартному виду I замечательного предела. Выполним замену переменной под знаком предела. Обозначим  – x = t. Тогда при x   новая переменная t  0. Кроме того,

² – x² = ² – ( – t)² = t(2 – t)

и

1 – sin = 1 – sin = 1 – sin = 1 – cos = 1 – (1 – 2sin²) = 2sin².

Теперь

= =   = 10 = 0.

Ответ: а) = ; б) = 0.

ИДЗ-7. Исследование функции на непрерывность

Исследовать данную функцию на непрерывность и построить ее график:

Решение: Функция f(x) определена и непрерывна на трех интервалах (–; 0), (0; 2) и (2; +), где она задана непрерывными элементарными функциями. Следовательно, разрыв функции возможен лишь в точках x₁ = 0 и x₂ = 2. Исследуем f(x) на непрерывность в них.

Точка x₁ = 0. Для этой точки f(x₁ = 0) = 0² = 0. Предел слева: A₁ = = . Предел справа: A₂ = =  A₁. Таким образом, функция f(x) в точке x₁ = 0 имеет (неустранимый) разрыв I рода. Точка x₂ = 2. Для этой точки f(x₂ = 2) = (x – 1)² = 1. Предел слева: A₁ = = . Предел справа: A₂ = =  A₁. Таким образом, функция f(x) в точке x₂ = 2 также имеет (неустранимый) разрыв I рода. График f(x) дан на рис. 1.

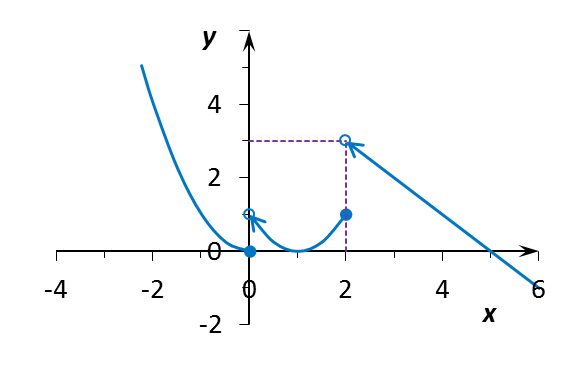
Рис. 1.

Ответ: Функция f(x) (рис. 1) претерпевает разрывы I рода в точках x₁ = 0 и x₂ = 2.

ИДЗ-8. Дифференцирование функций.

Продифференцировать данные функции:

а) y = 9x⁵ – + – 3x + 4; б) y = tg⁵(x+2)arccos3x²; в) y = .

Решение: Выполним задание, используя теоремы о производных и таблицу производных.

а) y = (9x⁵ – + – 3x + 4) = (9x⁵) – (4x^–3) + (x^7/3) – (3x) + (4) =

= 95x⁴ – 4(–3)x^–4 + x^4/3 – 3 + 0 = 45x⁴ + + – 3.

б) Заметим, что y = (uv) = uv + uv, где u = tg⁵(x+2) и v = arccos3x². Вычислим производные для функций u(x) и v(x):

u = (tg⁵(x+2)) = 5tg⁴(x+2)(tg(x+2)) = 5tg⁴(x+2) = 5tg⁴(x+2);

v = (arccos3x²) = – = – ;

Остается «собрать» окончательное выражение:

y = uv + uv = 5tg⁴(x+2)arccos3x² – tg⁵(x+2).

в) Как и в предыдущем примере, запишем y = (uv) = uv + uv, где u = и v = . Вычислим производные для функций u(x) и v(x):

u = () = = ;

v = () = (x⁴) = 4x³;

Остается «собрать» окончательное выражение:

y = uv + uv =  – 4x³.

Ответ: а) y = 45x⁴ + + – 3; б) y = 5tg⁴(x+2)arccos3x² – tg⁵(x+2); в) y =  – 4x³.

ИДЗ-9. Вычисление производных.

а) Найти y и y; б) для данной функции y(x) и точки x₀ вычислить y(x₀):

а) x³y – y² = 6x; б) y = ⅛ – ¼ cos²x, x₀ = /4.

Решение: а) Продифференцируем по x обе части равенства:

(x³y) – (y²) = (6x);

3x²y + x³y – 2yy = 6,

откуда

y = .

Продифференцируем по x обе части равенства 3x²y + x³y – 2yy = 6 еще раз:

(3x²y) + (x³y) – (2yy) = (6);

6xy + 3x²y + 3x²y + x³y – 2y² – 2yy = 0,

откуда

y(x³ – 2y) = 2y² – 6x²y – 6xy.

Подставляя теперь вместо y полученное выше выражение, имеем окончательно:

y = 2 – 6x² – .

б) Продифференцируем последовательно данную функцию y(x):

y = (⅛ – ¼ cos²x) = –¼2cos x(–sin x) = ¼sin 2x;

y = (¼sin 2x) = ¼2cos 2x = ½cos 2x;

y = (½cos 2x) = –½2sin 2x = –sin 2x.

Теперь легко получаем: y(x₀ = /4) = –sin(2/4) = –sin(/2) = –1.

Ответ: y = –sin 2x; y(x₀ = /4) = –1.

ИДЗ-10. Правило Лопиталя.

Найти указанные пределы, используя правило Лопиталя:

а) ; б) ; в) .

Решение: а) При x   числитель и знаменатель дроби под знаком предела стремятся к бесконечности, так что имеем неопределенность вида {/}, которую раскроем с помощью правила Лопиталя:

= = =  =  =

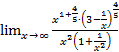=  = 0 = 0.

б) При x  числитель и знаменатель дроби под пределом стремятся к нулю, так что имеем неопределенность вида {0/0}, которую раскроем с помощью правила Лопиталя:

= = = –  = –  =

= – = .

в) При x  0 выражение под знаком предела стремится к неопределености вида 1^, для раскрытия которой не может быть непосредственно применено правило Лопиталя, и выражение следует предварительно преобразовать. Предположим, что предел существует и равен A = . Тогда

lnA = = = = =

= –  = – 11 = – .

Следовательно, A = e^–1/2 = .

Ответ: а) = 0; б) = ; в) = .

ИДЗ-11. Полное исследование функции и построение ее графика.

Провести полное исследование указанных функций и построить их графики:

а) y = ; б) y = – .

Решение: Полное исследование функций и построение их графиков проведем, придерживаясь следующей примерной схемы:

1. Указать область D определения функции f(x);

2. Найти (если они существуют) точки разрыва функции, точки пересечения ее графика с осями координат и вертикальные асимптоты;

3. Установить наличие или отсутствие четности/нечетности, периодичности f(x);

4. Исследовать функцию на монотонность и экстремум;

5. Определить интервалы выпуклости и вогнутости, точки перегиба;

6. Найти наклонные (горизонтальные) асимптоты графика функции;

7. Произвести необходимые дополнительные вычисления, уточняющие ход f(x);

8. Построить график y = f(x) в масштабе, правильно отражающем установленные особенности поведения функции.

а) Проведем полное исследование функции y = f(x) = , придерживаясь рекомендуемой схемы.

1. Функция f(x) определена для всех действительных x  R, т.е. D = R.

2. Функция не имеет точек разрыва, т.е. является непрерывной всюду на области D своего определения. Функция пересекает ось Ox в точках x₀₁ = –3 и x₀₂ = 0, т.е. нулями функции y = f(x) = 0 являются точки x₀₁ = –3 и x₀₂ = 0. Функция пересекает ось Oy (здесь x = 0) в точке y = 0. Отсутствие точек разрыва функции указывает также на отсутствие вертикальных асимптот у графика y(x).

3. Функция f(x) не является четной или нечетной, не является периодической, т.е. является функцией общего вида.

4. Для исследования функции на монотонность и экстремум вычислим ее первую производную:

y = () =  =  = .

Точками, подозрительными на экстремум (там, где производная y(x) равна нулю или не существует) являются точки x₁ = –3; x₂ = –2; x₃ = 0. Эти три особые точки разбивают область определения функции D на четыре (непересекающихся) интервала: D₁ = (–; –3), D₂ = (–3; –2), D₃ = (–2; 0), D₄ = (0; +). Изучим каждый из них.

Интервал D₁ = (–; –3). Здесь y > 0 и функция y = f(x) возрастает.

Интервал D₂ = (–3; –2). Здесь y > 0; функция y = f(x) возрастает.

Интервал D₃ = (–2; 0). Здесь y < 0 и функция y = f(x) убывает.

Интервал D₄ = (0; +). Здесь y > 0; функция y = f(x) возрастает.

Знак первой производной y(x) изменяется c «+» на «–» в точке x₂ = –2; в этой точке функция y = f(x) достигает (локального) максимума, равного y_max = f(–2) = =  1,587. В самой точке x₂ производная y(x₂ = –2) = 0.

Знак первой производной y(x) изменяется c «–» на «+» в точке x₃ = 0; в этой точке функция y = f(x) достигает (локального) минимума, равного y_min = 0. В самой точке x₂ производная y(x₂ = 0)  , т.е. касательная к графику функции y(x) в точке x₃ = 0 вертикальна.

В точке x₁ = –3 изменения знака первой производной не происходит, т.е. функция f(x) не имеет максимума или минимума. В самой точке x₁ производная y(x₁ = –3)  , т.е. касательная к графику функции y(x) в точке x₃ = 0 вертикальна.

5. Для определения интервалов выпуклости и вогнутости и точек перегиба вычислим вторую производную функции, как производную отношения:

y = () = = =

= = = – .

Точками, подозрительными на перегиб (там, где вторая производная y(x) равна нулю или не существует) являются точки x₁ = –3; x₃ = 0. В данном случае точки, в которых y(x) = 0, отсутствуют.

В области – < x < –3 вторая производная y > 0 и функция y = f(x) выпукла вниз (вогнута). В области –3 < x < 0 вторая производная y < 0 и функция y = f(x) выпукла вверх (выпукла). В области 0 < x < + вторая производная y < 0 и функция y = f(x) также выпукла вверх. Так как в точке x₁ = –3 вторая производная y меняет знак с «+» на «–», то точка x₁ является точкой перегиба.

6. Найдем наклонные (горизонтальные) асимптоты графика функции; как указано выше, вертикальных асимптот график функции y(x) не имеет. Как известно, наклонная асимптота имеет вид y = kx + b, коэффициенты k и b которой могут быть найдены как пределы:

k = ; b = .

В данном случае,

k = = = = 1;

b = = { – } = = = .

Для вычисления последнего предела удобно сделать замену переменной t = . При x   новая переменная t  0. Теперь, используя правило Лопиталя, имеем окончательно

b = = = = = 1.

Таким образом, график y(x) исследуемой функции имеет единственную наклонную асимптоту y = x + 1.

7. Необходимости в дополнительных вычислениях для уточнения поведения графика функции y(x) нет. Можно, однако, заметить дополнительно, что y(x) < 0 при x < –3; при x > –3, напротив, y(x) > 0.

8. Объединяя результаты проведенных выше исследований, строим график функции y = f(x) (рис. 2).

Рис. 2

б) Проведем полное исследование функции y = f(x) = – x, как и прежде придерживаясь рекомендуемой схемы.

1. Функция f(x) определена для всех действительных x > 0, т.е. D = (0; +).

2. Функция не имеет точек разрыва, т.е. является непрерывной всюду на области D своего определения, однако, при x  0 + 0 f(x)  – . Линия x = 0, т.е. ось Oy, является вертикальной асимптотой графика y(x). Для нахождения нулей функции y = f(x) следует решить уравнение

– x = 0,