ФГБОУ ВПО Уральский государственный педагогический университет

Математический факультет

В.Ю. Бодряков

Индивидуальные домашние задания (ИДЗ)

по дисциплине «Теория вероятностей и Математическая статистика»

Часть 2

Екатеринбург – 2012

Введение

Настоящая методическая разработка предназначена для студентов всех направлений подготовки всех форм обучения, изучающих дисциплину «Теория вероятностей и математическая статистика (ТВиМС)». Разработка содержит индивидуальные домашние задания (ИДЗ) по 30 вариантов в каждом и методические указания по их решению. Отчеты по ИДЗ в настоящей части разработки должны быть подготовлены в электронном виде и представлены публично либо в виде завершенной презентации, либо в виде оформленного текстового документа с включением необходимых таблиц, формул и графических элементов.

Методические указания к решению задач

ИДЗ-7. Закон распределения вероятностей дискретной случайной величины (д.с.в.). Числовые характеристики распределения д.с.в.

Задача 7. Составить закон распределения вероятностей дискретной случайной величины (д.с.в.) X – числа k выпадений хотя бы одной «шестерки» в n = 8 бросаниях пары игральных кубиков. Построить многоугольник распределения. Найти числовые характеристики распределения (моду распределения, математическое ожидание M(X), дисперсию D(X), среднее квадратическое отклонение (X)).

Решение: Введем обозначение: событие A – «при бросании пары игральных кубиков шестерка появилась хотя бы один раз». Для нахождения вероятности P(A) = p события A удобнее вначале найти вероятность P(Ā) = q противоположного события Ā – «при бросании пары игральных кубиков шестерка не появилась ни разу».

Поскольку вероятность непоявления «шестерки» при бросании одного кубика равна 5/6, то по теореме умножения вероятностей

P(Ā) = q = = .

Соответственно,

P(A) = p = 1 – P(Ā) = .

Испытания в задаче проходят по схеме Бернулли, поэтому д.с.в. величина X подчиняется биномиальному закону распределения вероятностей:

P_n(k) = pⁿq^n–k,

где = – число сочетаний из n по k. Проведенные для данной задачи расчеты удобно оформить в виде таблицы (табл. 4):

Таблица 4

Распределение вероятностей д.с.в. X (n = 8; p = 11/36; q = 25/36)

k	0	1	2	3	4	5	6	7	8	
	1	8	28	56	70	56	28	8	1
Pn(k)	0,0541	0,1904	0,2932	0,258	0,1419	0,05	0,011	0,0013	0,0001	1

Многоугольник распределения вероятностей представлен на рис. 2:

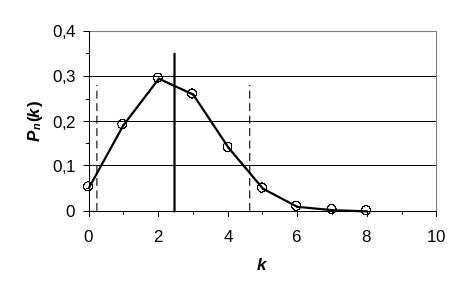
Рис. 2. Многоугольник распределения вероятностей д.с.в. X. Вертикальными линиями показаны числовые характеристики распределения: M(X) и M(X)  (X).

Найдем числовые характеристики распределения вероятностей д.с.в. X. Мода распределения равна 2 (здесь P₈(2) = 0,2932 максимально). Математическое ожидание равно:

M(X) = = 2,4444,

где x_k = k – значение, принимаемое д.с.в. X. Дисперсию D(X) распределения найдем по формуле:

D(X) = = 4,8097.

Среднее квадратическое отклонение (СКО):

(X) = = 2,1931.

Для наглядности математическое ожидание M(X) д.с.в. X, характеризующее «центр тяжести» распределения, показано на рис. 2 вертикальной сплошной линией. Здесь же пунктиром показаны линии M(X)  (X), характеризующие ширину распределения.

Ответ: Многоугольник распределения см. на рис. 2. Мода распределения равна 2; математическое ожидание M(X) = 2,4444; дисперсия D(X) = 4,8097; СКО (X) = 2,1931.

З а м е ч а н и е. Результаты расчетов можно интерпретировать следующим образом. При неоднократном проведении серий опытов по 8-ми кратному бросанию пары игральных кубиков число k выпадений хотя бы одной «шестерки» в большинстве (почти в 90%) случаев будет лежать в границах от 1 до 4.

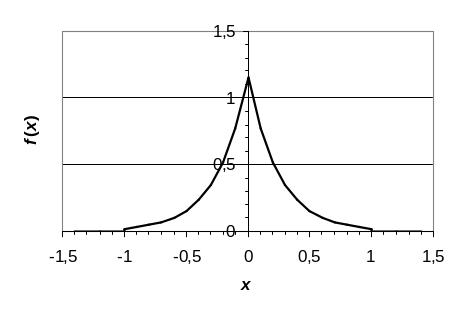
Задача 8. Для непрерывной случайной величины (н.с.в.) X задана плотность функции распределения: f(x) = С₁exp(–2|x|) при |x|  1; при |x| > 1 f(x) = 0. Нормировать плотность распределения. Вычислить функцию распределения F(x). Построить графики обеих функций. Вычислить числовые характеристики распределений: математическое ожидание M(X), дисперсию D(X), СКО (X). Вычислить вероятность того, что н.с.в. X примет значения из заданного интервала (a; b) = (1/2; 3/2).

Решение: Прежде всего, нормируем на единицу плотность функции распределения f(x); отсюда определится неизвестная постоянная С₁:

= 1 = = 2 = –С₁ = С₁(1 – e^–2),

откуда

С₁ =  1,1565.

При вычислении интеграла использована четность подынтегральной функции. Функцию распределения F(x) найдем путем интегрирования, причем здесь, в силу свойств функции y = |x| потребуется различать случаи x < 0 и x  0.

При –1  x < 0:

F(x) = = =   = ;

при 0  x  1:

F(x) = = + =

= F(0) + = +   = + ,

При x < –1 F(x) = 0; при x > 1 F(x) = 1.

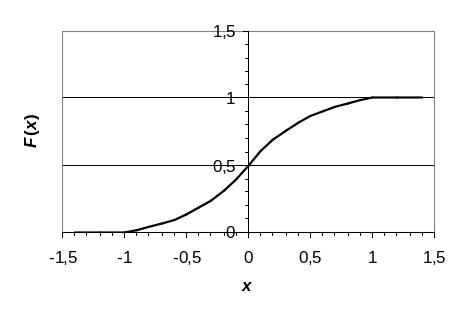
Графики плотности функции распределения f(x) и самой функции распределения F(x) представлены на рис. 3 и рис. 4, соответственно.

Рис. 3. График плотности функции распределения вероятностей f(x) н.с.в. X

Рис. 4. График функции распределения вероятностей F(x) н.с.в. X

Рассчитаем числовые характеристики распределения н.с.в. X. Математическое ожидание M(X) н.с.в. X равно:

M(X) = = = 0

в силу нечетности подынтегральной функции. Дисперсия D(X) н.с.в. X равна:

D(X) = = = 2 С₁ =  0,1870.

Интеграл в выражении для дисперсии берется двойным интегрированием по частям:

= (1 – 5e^–2)  0,0808.

Среднее квадратическое отклонение СКО найдем как

(X) = = 0,4324.

Наконец, вероятность того, что н.с.в. X примет значения из заданного интервала (a; b) = (1/2; 3/2) вычислим, воспользовавшись найденной функцией распределения:

P(1/2 < x < 3/2) = F(3/2) – F(1/2) = 1 – – =  0,1345.

Ответ: Графики плотности функции распределения f(x) и самой функции распределения F(x) н.с.в. X приведены на рис. 3, 4, соответственно. Вероятность попадания X в интервал (1/2; 3/2) равна P(1/2 < x < 3/2) = 0,1345. Числовые характеристики распределений: математическое ожидание M(X) = 0; дисперсия D(X) = 0,1870; СКО (X) = 0,4324.

Задача 9. Станок - автомат изготавливает валки с проектным контролируемым диаметром (случайная величина (с.в.) X), a = a₀ = 9 мм. Измерения n = 40 случайно отобранных для контроля изделий дали следующие результаты:

xi, мм	8,94	8,95	8,96	8,97	8,98	8,99	9,00	9,01	9,02	9,03	Прим.
ni	1	1	2	5	8	9	7	4	2	1	n = Sni = 40

Представить распределение валков по диаметру в виде гистограммы и оценить его основные числовые параметры. Можно ли считать, что распределение с.в. X соответствует нормальному закону распределения?

Гипотеза H₀₁: закон распределения с.в. X соответствует нормальному закону.

Гипотеза H₁₁: закон распределения с.в. X значимо отличен от нормального.

Обеспечивает ли станок изготовление деталей в проектном размере, или имеется систематическое занижение диаметра валков и требуется дополнительная настройка технологического процесса?

Гипотеза H₀₂: a = a₀ = 9 мм.

Гипотеза H₁₂: a < a₀.

Уровень значимости a = 0,05.

Решение: Распределение валков по диаметру представлено в виде гистограммы на рис. 5.

Рис. 5. Эмпирическое частотное распределение валков с.в. X.

Из рис. 5 видно, что, действительно, эмпирическое частотное распределение имеет куполообразный вид, характерный для нормального распределения. Центр эмпирического распределения, очевидно, смещен несколько влево относительно номинального диаметра a₀ = 9 мм. Для того, чтобы дать обоснованный ответ на вопрос о том, действительно ли соответствует наблюдаемое эмпирическое частотное распределение валков по диаметру нормальному закону распределения, используем критерий согласия ²-Пирсона.

Для того, чтобы иметь возможность вычисления теоретических частот, оценим параметры предполагаемого теоретического нормального распределения

N(x; a; ²) = .

Примем в качестве оценок параметров нормального распределения величины, вычисленные из самой выборки. А именно, приняв в качестве a среднее по выборке x_ср:

a = x_ср =  8,988

и приняв в качестве  квадратный корень из исправленной дисперсии:

 = s =  0,0191.

Относительные расчетные (теоретические) частоты n_calc вычислим как

n_i, _теор= n N(x_i; a; ²)∆x,

где ∆x = 0,01 – шаг по диаметру в частотном эмпирическом распределении. Результаты расчетов сведены в табл. 5:

Таблица 5

Эмпирические и расчетные частоты распределения валков по диаметру. Подсчет критерия Пирсона ².

N п/п	xi	ni	ni, теор	ni – ni, теор	(ni – ni, теор)2/ ni, теор
1	8,94	1	0,3561	0,6439	1,1646
2	8,95	1	1,1561	-0,1561	0,0211
3	8,96	2	2,8542	-0,8542	0,2557
4	8,97	5	5,3587	-0,3587	0,0240
5	8,98	8	7,6504	0,3496	0,0160
6	8,99	9	8,3056	0,6944	0,0581
7	9	7	6,8566	0,1434	0,0030
8	9,01	4	4,3043	-0,3043	0,0215
9	9,02	2	2,0548	-0,0548	0,0015
10	9,03	1	0,7459	0,2541	0,0866
		40			1,652

Таким образом, эмпирическое значение критерия Пирсона составляет  1,652. Согласно правилам проверки статистических гипотез требуется сравнить эмпирическую величину критерия с табличным критическим значением . Для определения последнего вычислим число степеней свободы: k = s – 1 – r, где s – число групп выборки; r – число параметров теоретического распределения, оцениваемых на основании самой эмпирической выборки. В нашем случае s = 10 и r = 2 (на основании выборки оценивались параметры нормального распределения a и ). В итоге k = 10 – 1 – 2 = 7. По таблице распределения Пирсона ² находим = = 14,1. Так как < , то нулевую гипотезу H₀₁ принимаем и можем утверждать, что закон распределения с.в. X соответствует нормальному закону. Данный вывод наглядно подтверждает рис. 6. Вместе с тем видно, что центр распределения смещен влево относительно проектного размера.

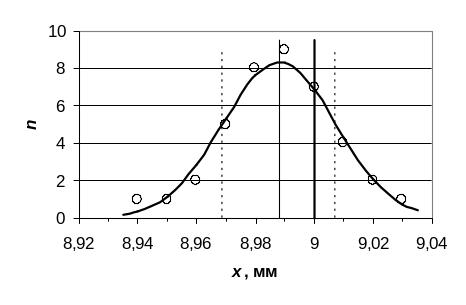
Рис. 6. Эмпирическое частотное распределение валков с.в. X в сопоставлении с теоретическим нормальным распределением (сплошная линия). Вертикальные прямые показывают проектный диаметр (жирная линия); эмпирический средний диаметр (тонкая линия)  исправленное СКО (пунктир).

Для ответа на вопрос о значимости смещения среднего диаметра относительно проектного размера a₀ = 9 мм применим T-критерий Стьюдента, который вычисляется по формуле:

T = ,

где, как и выше, x_ср = 8,988 мм – средний фактический диаметр валков; a₀ = 9 мм – проектный размер; n = 40 – объем выборки; s = 0,0191 – исправленное СКО. В нашем случае эмпирическое значение T_эмп = –3,9718. Критическое значение t_кр найдем по таблице t-распределения Стьюдента для уровня значимости  = 0,05 и числа степеней свободы k = n – 1 = 39: t_кр(; k) = t_кр(0,05; 39) = 1,68. Согласно правилу применения левостороннего T-критерия Стьюдента, если T_эмп < – t_кр, то нулевая гипотеза H₀₂ на принятом уровне значимости  = 0,05 должна быть отвергнута и принята конкурирующая H₁₂: a < a₀, – фактический средний диаметр валков a значимо меньше проектного размера a₀. В производственной практике это свидетельствует о необходимости дополнительной настройки технологического процесса в сторону увеличения диаметра изготавливаемых изделий (примерно на +0,012 мм).

Ответ: На уровне значимости  = 0,05 можно считать, что эмпирическое распределение диаметров валков соответствует нормальному закону распределения. Средний диаметр валков a значимо меньше проектного размера a₀; требуется дополнительная настройка технологического процесса в сторону увеличения диаметра изготавливаемых валков.

Задача 10. В исследовании, посвященном проблемам ценностных приоритетов, выявлялись иерархии жизненных (терминальных) ценностей (ТЦ) по методике Рокича у родителей и их взрослых детей. Ранги терминальных ценностей, полученные при обследовании пары мать (ряд A) – дочь (ряд B) приведены в таблице:

№ ТЦ	A: Ранг ценностей в иерархии матери, xi	B: Ранг ценностей в иерархии дочери, yi
1. Активная деятельная жизнь	15	15
2. Жизненная мудрость	1	3
3. Здоровье	7	14
4. Интересная работа	8	12
5. Красота природы и искусство	16	17
6. Любовь	11	10
7. Материально обеспеченная жизнь	12	13
8. Наличие хороших и верных друзей	9	11
9. Общественное признание	17	5
10. Познание	5	1
11. Продуктивная жизнь	2	2
12. Развитие	6	8
13. Развлечения	18	18
14. Свобода	4	6
15. Счастливая семейная жизнь	13	4
16. Счастье других	14	16
17. Творчество	10	9
18. Уверенность в себе	3	7

Коррелируют ли терминальные ценности матери и дочери? Найти выборочные коэффициенты ранговой корреляции Спирмена и Кендалла и проверить статистическую гипотезу о значимости каждого из них. Сравнить полученные результаты. Уровень значимости  = 0,05.

Решение: Выборочный коэффициент ранговой корреляции Спирмена R_S определим по формуле

R_S = 1 – ,

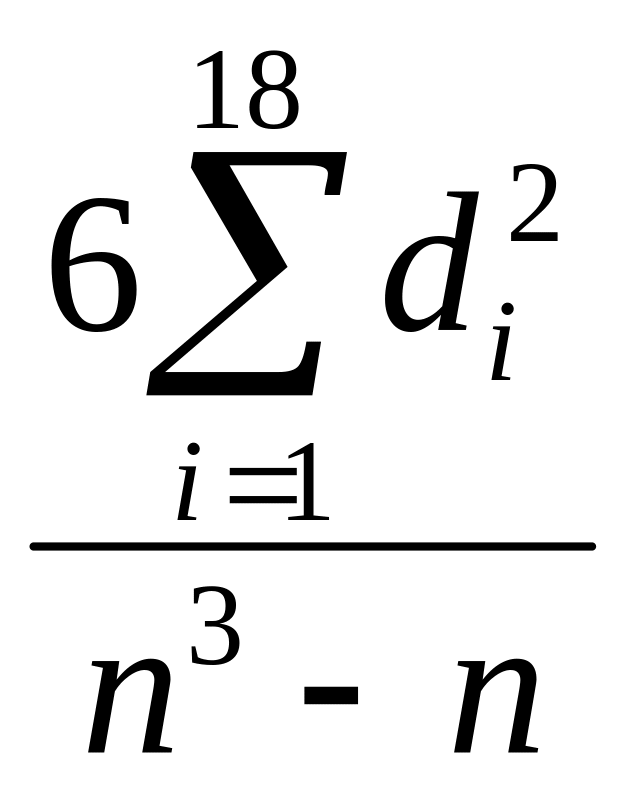где d_i = x_i – y_i; n = 18 – объем выборки. Ранговые разности d_i приведены в табл. 6

Таблица 6

Ранговые разности для подсчета коэффициента ранговой корреляции R_S Спирмена.

№ ТЦ	xi	yi	di = xi – yi	di2
1	15	15	0	0
2	1	3	-2	4
3	7	14	-7	49
4	8	12	-4	16
5	16	17	-1	1
6	11	10	1	1
7	12	13	-1	1
8	9	11	-2	4
9	17	5	12	144
10	5	1	4	16
11	2	2	0	0
12	6	8	-2	4
13	18	18	0	0
14	4	6	-2	4
15	13	4	9	81
16	14	16	-2	4
17	10	9	1	1
18	3	7	-4	16
			0	346

На основании данных табл. 6 вычисляем R_S = 1 –  0,643. Как и должно быть, –1  R_S  1.

Для проверки значимости найденного значения R_S, выдвинем следующие статистические гипотезы:

Гипотеза H₀: коэффициент корреляции Спирмена R_S = 0.

Гипотеза H₁: коэффициент корреляции Спирмена R_S  0.

Для того, чтобы при уровне значимости  проверить нулевую гипотезу H₀ о равенстве нулю генерального коэффициента ранговой корреляции R_S Спирмена при конкурирующей гипотезе H₁ (R_S  0), надо вычислить критическую точку

T_кр = t_кр(; k) ,

где t_кр(; k) – критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента по уровню значимости  и числу степеней свободы k = n – 2. В нашем случае t_кр(0,05; 16) = 2,12 и T_кр  0,406. Так как эмпирическое значение коэффициента корреляции Спирмена превышает критическое: R_S > T_кр, то нулевую гипотезу отвергаем и принимаем конкурирующую: между качественными признаками A и B существует значимая ранговая корреляционная связь.

Выборочный коэффициент ранговой корреляции Кендалла R_K определим по формуле

R_K = – 1,

где R = R₁ + R₂ + ... + R_n–1 – сумма рангов. Для подсчета суммы рангов R упорядочим эмпирическую таблицу так, чтобы один из качественных признаков, например, A, был упорядочен, например, в порядке убывания значимости (табл. 7).

Таблица 6

Ранговые разности для подсчета коэффициента ранговой корреляции R_K Кендалла.

№ ТЦ	xi	yi	Ri	Значения yi+1 > xi, i = 1, 2, …, n–1
2	1	3	16	2; 7; 6; 8; 14; 12; 11; 9; 10; 13; 4; 16; 15; 17; 5; 18
11	2	2	15	7; 6; 8; 14; 12; 11; 9; 10; 13; 4; 16; 15; 17; 5; 18
18	3	7	14	6; 8; 14; 12; 11; 9; 10; 13; 4; 16; 15; 17; 5; 18
14	4	6	12	8; 14; 12; 11; 9; 10; 13; 16; 15; 17; 5; 18
10	5	1	11	8; 14; 12; 11; 9; 10; 13; 16; 15; 17; 18
12	6	8	10	14; 12; 11; 9; 10; 13; 16; 15; 17; 18
3	7	14	9	12; 11; 9; 10; 13; 16; 15; 17; 18
4	8	12	8	11; 9; 10; 13; 16; 15; 17; 18
8	9	11	6	10; 13; 16; 15; 17; 18
17	10	9	5	13; 16; 15; 17; 18
6	11	10	5	13; 16; 15; 17; 18
7	12	13	4	16; 15; 17; 18
15	13	4	4	16; 15; 17; 18
16	14	16	3	15; 17; 18
1	15	15	2	17; 18
5	16	17	1	18
9	17	5	1	18
13	18	18	–	–
			0	346

Ранг R₁ определяется количеством рангов y_i, превышающих ранг x₁ = 1. Всего таких рангов R₁ = 16; а именно, {2; 7; 6; 8; 14; 12; 11; 9; 10; 13; 4; 16; 15; 17; 5; 18}. Продолжая процедуру подсчета R_i (см. табл. 6), получим R = = 126. В итоге, R_K = – 1  0,647. Как и должно быть, –1  R_K  1.

Для проверки значимости найденного значения R_K, выдвинем следующие статистические гипотезы:

Гипотеза H₀: коэффициент корреляции Кендалла R_K = 0.

Гипотеза H₁: коэффициент корреляции Кендалла R_K  0.

Для того, чтобы при уровне значимости  проверить нулевую гипотезу H₀ о равенстве нулю генерального коэффициента ранговой корреляции R_K Кендалла при конкурирующей гипотезе H₁ (R_K  0), надо вычислить критическую точку

T_кр = z_кр ,

где z_кр – критическая точка двусторонней критической области, которую находят по таблице функции Лапласа по равенству (z_кр) = (1 – )/2. В нашем случае (z_кр) = 0,475, откуда z_кр = 1,96 и T_кр  0,338. Так как эмпирическое значение коэффициента корреляции Кендалла превышает критическое: R_K > T_кр, то нулевую гипотезу отвергаем и принимаем конкурирующую: между качественными признаками A и B существует значимая ранговая корреляционная связь.

Как видно из расчетов, выборочные коэффициенты ранговой корреляции Спирмена и Кендалла близки друг к другу, так что для оценки степени корреляционной связи между двумя наборами качественных признаков может быть использован любой из них.

Ответ: На уровне значимости  = 0,05 можно считать, что терминальные ценности матери и дочери находятся в значимой корреляционной связи друг с другом. Значения выборочных коэффициентов ранговой корреляции Спирмена и Кендалла равны, соответственно, R_S = 0,643 и R_K = 0,647.

Варианты индивидуальных домашних заданий (ИДЗ)

ИДЗ-7. Закон распределения вероятностей дискретной случайной величины (д.с.в.). Числовые характеристики распределения д.с.в.

Составить закон распределения вероятностей д.с.в. X. Построить многоугольник распределения. Найти числовые характеристики распределения (моду распределения, математическое ожидание M(X), дисперсию D(X), среднее квадратическое отклонение (X)).

1. Монета подбрасывается до тех пор, пока герб не выпадет второй раз, при этом делается не более 4 проб. Д.с.в. X – число подбрасываний.

2. Две монеты подброшены n = 4 раза. Д.с.в. X – число выпадений двух «гербов» в n бросаниях.

3. Среди 5 ключей два подходят к двери. Ключи пробуют один за другим, пока не откроют дверь. Найти распределение вероятностей для числа опробованных ключей. Д.с.в. X – число опробованных ключей.

4. Игральный кубик брошен n = 6 раз. Д.с.в. X – количество выпадений очков, кратных двум или трем.

5. Два игральных кубика брошены n = 6 раз. Д.с.в. X – число выпадений пар, содержащих ровно одну «четверку» в n бросаниях.

6. Два игральных кубика бросаются n = 12 раз с подсчетом сумм выпавших очков. Д.с.в. X – число сумм, кратных четырем.

7. Из ящика, содержащего N = 10 деталей, среди которых n = 6 стандартных деталей, наудачу вынимаются M = 4 детали. Д.с.в. X – число стандартных деталей в выборке.

8. Бросаются два игральных кубика. Д.с.в. X – сумма выпавших очков.

9. На элеватор прибыло N₁ = 6 машин агрофирмы АФ-1 и N₂ = 9 машин агрофирмы AФ-2. Под разгрузку случайным образом загоняются n = 6 машин. Д.с.в. X – число разгружаемых машин агрофирмы АФ-1.

10. Вероятность того, что стрелок при одном выстреле из пистолета (в обойме n = 9 патронов) попадет в цель равна 0,8. Стрельба ведется до первого промаха. Д.с.в. X – число оставшихся в обойме патронов.

11. Игральный кубик брошен n = 8 раз. Д.с.в. X – число выпадений нечетного числа очков в n бросаниях.

12. В процессе производства изделие высшего качества удается получить только с вероятностью 0,2. С конвейера берутся наугад детали до тех пор, пока не будет взято изделие высшего качества. Д.с.в. X – число число проверенных изделий.

13. Бросаются два игральных кубика. Д.с.в. X – модуль разности выпавших очков.

14. Из ящика, содержащего N = 8 деталей, среди которых n = 5 стандартных деталей, наудачу вынимаются m = 3 детали. Д.с.в. X – число стандартных деталей в выборке.

15. Каждая из 5 лампочек имеет дефект с вероятностью 0,1. Дефектная лампочка при включении сразу перегорает и ее заменяют новой. Д.с.в. X – число опробованных ламп.

16. Прибор комплектуется из двух деталей, вероятность брака для первой детали – 0,1, а для второй – 0,05. Для контроля выбрано 4 прибора. Прибор бракуется, если в нем есть хотя бы одна бракованная деталь. Д.с.в. X – число бракованных приборов среди проверенных 4 приборов.

17. Вероятность того, что стрелок при одном выстреле из пистолета (в обойме n = 8 патронов) попадет в цель равна 2/3. Стрельба ведется до первого промаха. Д.с.в. X – число произведенных выстрелов.

18. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,2. Д.с.в. X – число отказавших элементов в одном опыте.

19. В партии из 15 деталей 20% деталей нестандартны. Наудачу отобраны три детали. Д.с.в. X – число нестандартных деталей среди трех отобранных.

20. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,7. Стрелку выдаются патроны до тех пор, пока он не промахнется. Д.с.в. X – число патронов, выданных стрелку.

21. Имеется 6 монет достоинством 10, 5, 5, 2, 1, 1 рублей. Наудачу берутся три монеты. Д.с.в. X – набранная этими монетами сумма.

22. Вероятность того, что лотерейный билет выигрышный, равна 0,1. Покупатель купил 5 билетов. Д.с.в. X – число выигрышей у владельца этих 5 билетов.

23. Два стрелка поражают мишень с вероятностями, соответственно, 0,8 и 0,9 (при одном выстреле), причем первый стрелок выстрелил один раз, а второй – два раза. Д.с.в. X – общее число попаданий в мишень.

24. ОТК должен проверить 12 комплектов, состоящих из 4 изделий каждый, причем каждая деталь может быть стандартной с вероятностью 0,9. Д.с.в. X – число комплектов, состоящих из стандартных деталей.

25. В партии из 15 деталей 40% деталей нестандартны. Наудачу отобраны четыре детали. Д.с.в. X – число стандартных деталей среди четырех отобранных деталей.

26. Три стрелка с вероятностями попадания в цель при отдельном выстреле 0,7, 0,8 и 0,9, соответственно, делают по одному выстрелу. Д.с.в. X – общее число попаданий.

27. Из урны, в которой лежат 2 белых и 8 черных шаров, последовательно вынимают шары до тех пор, пока не появится белый шар. Д.с.в. X – число вынутых при этом шаров.

28. Стрелок поражает мишень с вероятностью 0,7 при одном выстреле. Стрелок стреляет до первого попадания, но делает не более четырех выстрелов. Д.с.в. X – число произведенных выстрелов.

29. Сдача зачета по математической статистике производится до получения положительного результата. Шансы сдать зачет остаются неизменными и составляют 60%. Д.с.в. X – число попыток сдачи зачета.

30. В шестиламповом усилителе перегорела одна лампа. Лампы заменяют новыми одну за другой, пока усилитель не заработает. Д.с.в. X – число замененных ламп.

ИДЗ-8. Закон распределения вероятностей непрерывной случайной величины (н.с.в.). Числовые характеристики распределения н.с.в.

Для непрерывной случайной величины (н.с.в.) X задана функция распределения F(x) (плотность функции распределения f(x)). Вычислить соответствующую плотность функции распределения f(x) (функцию распределения F(x)). Проверить выполнение условия нормировки распределений. Построить графики обеих функций. Вычислить числовые характеристики распределений: математическое ожидание M(X) и дисперсию D(X). Вычислить вероятность того, что н.с.в. X примет значения из заданного интервала (a; b).

Примечание: C₁, C₂ = сonst.

1. Функция распределения

 0 при x < –2,

F(x) =  ¼ x + С₁ при –2  x < 2,

 C₂ при 2  x.

Интервал (a; b) = (1; 2).

2. Плотность функции распределения

 0 при x < 1,

f(x) =  x + C₁ при 1  x < 2,

 0 при 2  x.

Интервал (a; b) = (–3/2; 3/2).

3. Функция распределения

 С₁ при x < 0,

F(x) =  ¼ x + С₂arcsin(½x) при 0  x < 2,

 1 при 2  x.

Интервал (a; b) = (1; 2).

4. Плотность функции распределения вероятностей н.с.в. X задана на числовой оси Ox выражением: f(x) = С₁exp(–x²). Интервал (a; b) = (–1; 1).

5. Функция распределения

 0 при x < 2,

F(x) =  ½ x + C₁ при 2  x < 4,

 1 при 4  x.

Интервал (a; b) = (–2; 3).

6. Плотность функции распределения вероятностей задана на числовой оси Ox выражением: f(x) = С₁exp(–(x–1)²/32). Интервал (a; b) = (0; 2).

7. Плотность функции распределения вероятностей н.с.в. X задана при x  1 выражением: f(x) = exp(1 – С₁x); при x < 1 плотность f(x) = 0. Интервал (a; b) = (0; 2).

8. Н.с.в. задана функцией распределения

 0 при x < 0,

F(x) =  C₁ x² + C₂ при 0  x < 2,

 1 при 2  x.

Интервал (a; b) = (¼; ¾).

9. Плотность функции распределения вероятностей н.с.в. X задана при x  0 выражением: f(x) = С₁exp(–3x) (С₁ > 0); при x < 0 плотность f(x) = 0. Интервал (a; b) = (0; 2).

10. Плотность функции распределения вероятностей задана при x  [0; ] выражением: f(x) = С₁sin² x; при x  [0; ] плотность f(x) = 0. Интервал (a; b) = (¼ ; ¾ ).

11. Функция распределения задана на всей числовой оси Ox выражением: F(x) = ½ + С₁arctg(½x). Интервал (a; b) = (0; 2).

12. Плотность функции распределения в промежутке (0; ) задана выражением: f(x) = С₁sin(¾ x); вне его – равна нулю. Интервал (a; b) = (0; ½ ).

13. Функция распределения

 0 при x < 0,

F(x) =  C₁sin x при 0  x < ½ ,

 C₂ при ½   x.

Интервал (a; b) = (/6; /3).

14. Плотность функции распределения вероятностей задана на числовой оси Ox выражением: f(x) = С₁exp(–½(x–1)²). Интервал (a; b) = (–1; 1).

15. Функция распределения

 0 при x < 0,

F(x) =  C₁cos x + C₂ при 0  x < ½ ,

 C₂ при ½   x.

Интервал (a; b) = (/6; /3).

16. Функция распределения задана на всей числовой оси Ox выражением: F(x) = ½ + С₁arctgx. Интервал (a; b) = (–1; 1).

17. Плотность функции распределения вероятностей н.с.в. X задана в промежутке (0; 1) выражением: f(x) = С₁(x² + 2x); вне этого промежутка f(x) = 0. Интервал (a; b) = (0; ½).

18. Плотность функции распределения вероятностей н.с.в. X задана в промежутке (–1; 1) выражением: f(x) = С₁ 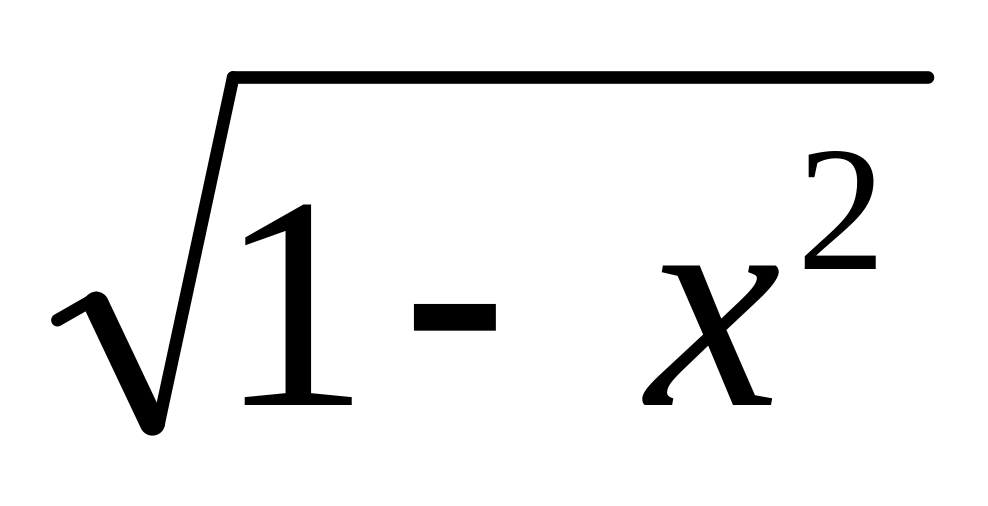; вне этого промежутка f(x) = 0. Интервал (a; b) = (0; ½).

19. Н.с.в. X равномерно распределена в промежутке (1; 4). Вне этого промежутка f(x) = 0. Интервал (a; b) = (1; 3).

20. Функция распределения вероятностей н.с.в. X задана при x  0 выражением: F(x) = С₁ – exp(–С₁x). Интервал (a; b) = (2; +).

21. Плотность функции распределения вероятностей н.с.в. X задана на числовой оси Ox выражением: f(x) = С₁e^–|x|. Интервал (a; b) = (–2; 2).

22. Плотность функции распределения вероятностей н.с.в. X задана в промежутке (–2; 2) выражением: f(x) = С₁/ 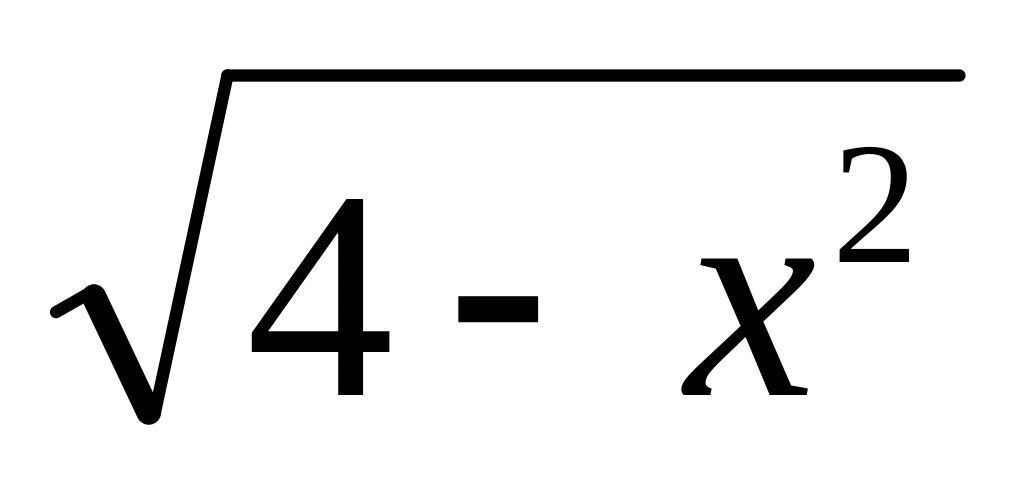; вне этого промежутка f(x) = 0. Интервал (a; b) = (1; +).

23. Н.с.в. X равномерно распределена в промежутке (–1; 3). Вне этого промежутка f(x) = 0. Интервал (a; b) определяется неравенством |x - 1| < 1.

24. Плотность функции распределения вероятностей н.с.в. X задана при x  0 выражением: f(x) = С₁exp(–2x); при x < 0 плотность распределения f(x) = 0. Интервал (a; b) = (0; 2).

25. Н.с.в. задана функцией распределения

F(x) =

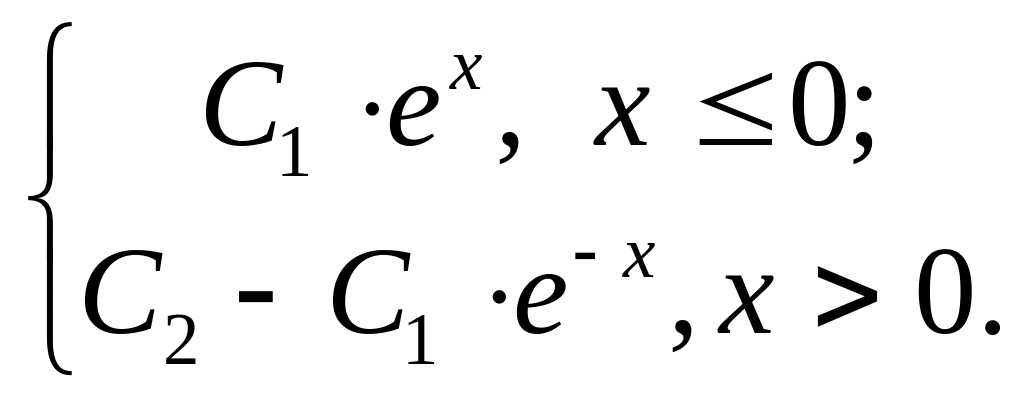
Интервал (a; b) = (–1; 3).

26. Плотность функции распределения вероятностей задана на числовой оси Ox выражением: f(x) = С₁exp(–(x–4)²/50). Интервал (a; b) = (0; 4).

27. Плотность функции распределения

f(x) =

Интервал (a; b) определяется неравенством |x| < 1.

28. Плотность функции распределения на числовой оси: f(x) = С₁ + 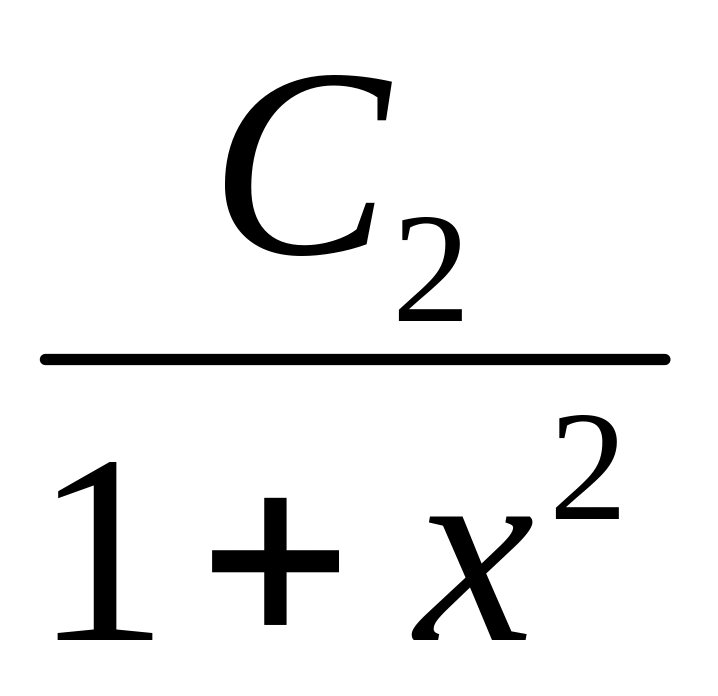(распределение Коши). Интервал (a; b) = (1; +).

29. Плотность функции распределения

f(x) =

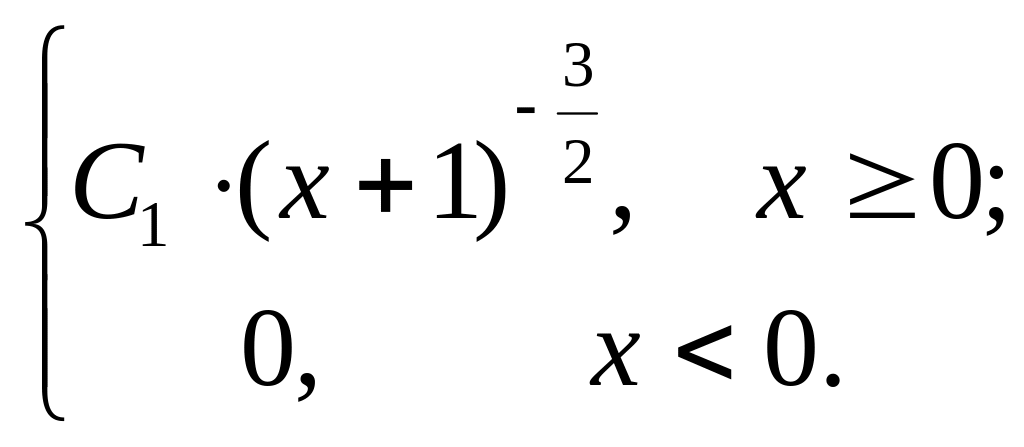
Интервал (a; b) определяется неравенством |x – ⅓| < 1.

30. Н.с.в. задана функцией распределения

 0 при x < 0,

F(x) =  C₁x – x² при 0  x < 1,

 1 при 1  x.

Интервал (a; b) = (–⅓; ⅓).

ИДЗ-9. Проверка статистических гипотез

Относительно случайной величины (с.в.) X (или двух с.в. X и Y) выдвинута основная статистическая гипотеза H₀, при конкурирующей гипотезе H₁. Применяя подходящий статистический критерий, выполнить проверку справедливости основной гипотезы на уровне значимости a = 0,05. При необходимости найти точечные выборочные оценки параметров распределения. Анализируемые распределения представить графически.

1. С.в. X (число семян сорняков в пробе зерна) задана эмпирическим рядом распределения:

xi	0	1	2	3	4	5	6	Прим.
ni	405	366	175	40	8	4	2	Sni = 1000

Гипотеза H₀: с.в. X имеет распределение Пуассона.

Гипотеза H₁: с.в. X распределена не по закону Пуассона.

2. С.в. X (число нестандартных деталей в n = 200 партиях) задана эмпирическим рядом распределения:

xi	0	1	2	3	4	Прим.
ni	132	43	20	3	2	Sni = 200

Гипотеза H₀: с.в. X имеет распределение Пуассона.

Гипотеза H₁: с.в. X распределена не по закону Пуассона.

3. С.в. X (число появлений события A в 10 опытах по 5 независимых испытаний) задана эмпирическим рядом распределения:

xi	0	1	2	3	4	Прим.
ni	5	2	1	1	1	Sni = 10

Гипотеза H₀: с.в. X имеет биномиальное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от биномиального.

4. С.в. X (время работы элемента электронного устройства) задана эмпирическим рядом распределения для n = 200 элементов:

xi	2,5	7,5	12,5	17,5	22,5	27,5	Прим.
ni	133	45	15	4	2	1	Sni = 200

где x_i – среднее время работы элемента в часах; n_i – количество элементов, проработавших в среднем x_i часов.

Гипотеза H₀: с.в. X имеет показательное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от показательного.

5. В 7 случаях из 10 фирма «B» – конкурент компании «А» действовала на рынке так, как будто ей заранее были известны решения, принимаемые фирмой «А». Определите, случайно ли это (гипотеза H₀), или в фирме «А» работает осведомитель фирмы-конкурента (гипотеза H₁)?

6. С.в. X (отклонение контролируемого размера изделия от номинала, мм) задана эмпирическим рядом распределения для n = 200 изделий:

xi	0,3	0,5	0,7	0,9	1,1	1,3	1,5	1,7	1,9	2,1	2,3	Прим.
ni	6	9	26	25	30	26	21	24	20	8	5	Sni = 200

Гипотеза H₀: с.в. X имеет нормальное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от нормального.

7. С.в. X (ошибка измерения дальности радиодальномером в метрах) задана эмпирическим рядом распределения для n = 200 измерений:

xi	3	5	7	9	11	13	15	17	19	21	Прим.
ni	21	16	15	26	22	14	21	22	18	25	Sni = 200

где x_i – ошибка измерения; n_i – количество измерений, с ошибкой x_i.

Гипотеза H₀: с.в. X имеет равномерное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от равномерного.

8. Время реакции на световой сигнал среди водителей - профессионалов должно находиться на уровне t₀ = 3 с для безопасной езды в темное время суток. Тесты, проведенные среди 16 водителей дали следующие результаты: t_ср = 4,5 с, s_t² = 16 c². Определите, значимо ли превышение среднего времени реакции t_ср над требуемым t₀ (гипотеза H₁), или это различие объясняется случайными причинами (гипотеза H₀)?

9. С.в. X (число появлений события A в 100 опытах по 10 независимых испытаний) задана эмпирическим рядом распределения:

xi	0	1	2	3	4	5	6	7	Прим.
ni	2	3	10	22	26	20	12	5	Sni = 100

Гипотеза H₀: с.в. X имеет биномиальное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от биномиального.

10. С.в. X (число поврежденных при перевозке стеклянных изделий в одном контейнере) задана эмпирическим рядом распределения:

xi	0	1	2	3	4	5	6	7	Прим.
ni	199	169	87	31	9	3	1	1	Sni = 500

Гипотеза H₀: с.в. X имеет распределение Пуассона.

Гипотеза H₁: с.в. X распределена не по закону Пуассона.

11. Двумя методами X и Y проведены измерения одной и той же физической величины. Получены следующие результаты:

xi	1,08	1,10	1,12	1,14	1,15	1,25	1,36	1,38	1,40	1,42
yi	1,11	1,12	1,18	1,22	1,33	1,35	1,36	1,38	–	–

Можно ли считать, что оба метода обеспечивают одинаковую точность измерений? Гипотеза H₀: D(X) = D(Y). Гипотеза H₁: D(X) ¹ D(Y).

12. Из нормальной генеральной совокупности с дисперсией s₀² = 0,18 извлечена выборка объема n = 31:

xi	10,1	10,3	10,6	11,2	11,5	11,8	12,0
ni	1	3	7	10	6	3	1

Верно ли, что выборочная дисперсия равна дисперсии генеральной совокупности? Гипотеза H₀: s₀² = s² = 0,18. Гипотеза H₁: s² > 0,18.

13. С.в. X (время безотказной работы элемента некоторого устройства) задана эмпирическим рядом распределения для n = 1000 элементов:

xi	5	15	25	35	45	55	65	Прим.
ni	365	245	150	100	70	45	25	Sni = 1000

где x_i – среднее время безотказной работы элемента в часах; n_i – количество элементов, проработавших в среднем x_i часов.

Гипотеза H₀: с.в. X имеет показательное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от показательного.

14. Точность работы станка - автомата проверяется по дисперсии контролируемого размера изделий, которая не должна превышать s₀² = 0,1. Взята проба из n = 36 случайно отобранных изделий. С.в. X – контролируемый размер изделий пробы:

xi	2,5	3,0	3,5	3,8	4,4	4,5	11,8	12,0	Прим.
ni	2	3	7	10	8	2	3	1	Sni = 36

Обеспечивает ли станок требуемую точность?

Гипотеза H₀: s₀² = s² = 0,1. Гипотеза H₁: s² > 0,1.

15. Двумя методами X и Y проведены измерения одной и той же физической величины. Получены следующие результаты:

а) в первом случае x₁ = 9,6; x₂ = 10,0; x₃ = 9,8; x₄ = 10,2; x₅ = 10,6;

б) во втором случае y₁ = 10,4; y₂ = 9,7; x₃ = 10,0; x₄ = 10,3.

Можно ли считать, что оба метода обеспечивают одинаковую точность измерений? Гипотеза H₀: D(X) = D(Y). Гипотеза H₁: D(X) ¹ D(Y).

16. В результате длительного хронометража времени сборки узла механизма различными сборщиками установлено, что дисперсия этого времени s₀² = 2 мин². Результаты n = 20 наблюдений за работой новичка таковы:

xi, мин	56	58	60	62	64	Прим.
ni	1	4	10	3	2	Sni = 20

Можно ли считать, что новичок работает в одном ритме с другими сборщиками? Гипотеза H₀: s₀² = s² = 2. Гипотеза H₁: s² > 2.

17. Из двух партий изделий, изготовленных на двух одинаково настроенных станках, извлечены малые выборки объемами n = 10 и m = 12. С.в. X и Y – контролируемые размеры изделий, изготовленных на первом и втором станках, соответственно:

xi	3,4	3,5	3,7	3,9	Прим.
ni	2	3	4	1	Sni = 10
yi	3,2	3,4	3,6	–
mi	2	2	8	–	Smi = 12

Считая, что с.в. X и Y имеют нормальное распределение, проверить гипотезу о равенстве средних размеров изделий, изготовленных на этих станках. Гипотеза H₀: M(X) = M(Y). Гипотеза H₁: M(X) ¹ M(Y).

18. Из двух партий изделий извлечены малые выборки объемами n = 10 и m = 16. С.в. X и Y – контролируемые размеры изделий, соответственно:

xi	12,3	12,5	12,8	13,0	13,5	Прим.
ni	1	2	4	2	1	Sni = 10
yi	12,2	12,3	13,0	–	–
mi	6	8	2	–	–	Smi = 16

Считая, что с.в. X и Y имеют нормальное распределение, проверить гипотезу о равенстве средних размеров изделий. Гипотеза H₀: M(X) = M(Y). Гипотеза H₁: M(X) > M(Y).

У к а з а н и е: предварительно проверить нулевую гипотезу о равенстве генеральных дисперсий H₀: D(X) = D(Y) при конкурирующей гипотезе H₁: D(X)  D(Y).

19. Проектный контролируемый размер изделий, изготавливаемых станком - автоматом, a = a₀ = 35 мм. Измерения n = 20 случайно отобранных изделий дали следующие результаты:

xi, мм	34,8	34,9	35,0	35,1	35,3	Прим.
ni	2	3	4	6	5	Sni = 20

Обеспечивает ли станок изготовление деталей в проектном размере?

Гипотеза H₀: a = a₀ = 35 мм. Гипотеза H₁: a ¹ a₀.

20. На двух аналитических весах, в одном и том же порядке, взвешены n = 10 проб химического вещества (с.в. X и Y, соответственно) и получены следующие результаты взвешиваний (в мг):

xi	25	30	28	50	20	40	32	36	42	38
yi	28	31	26	52	24	36	33	35	45	40

В предположении, что обе с.в. распределены нормально, проверить, значимо или незначимо различаются результаты взвешиваний?

Гипотеза H₀: M(X) = M(Y). Гипотеза H₁: M(X) ¹ M(Y).

21. Почва двух участков земли была тщательно проанализирована и оказалась одинаковой по составу. На этих участках посеяли пшеницу одного сорта. На участке 1 было внесено удобрение, а на участке 2 – нет. К моменту сбора урожая с каждого участка была произведена случайная выборка 50 растений и измерена их длина. После статистической обработки выборок X и Y были получены следующие оценки: 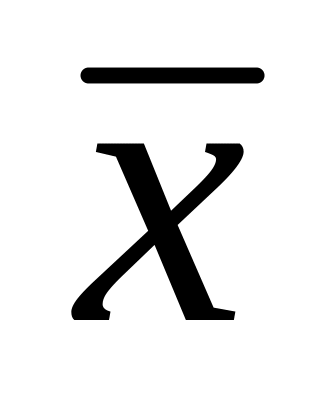= 323 мм, 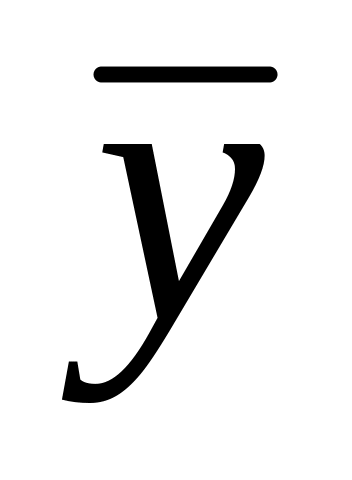= 297 мм, s_x² = 441 мм², s_y² = 529 мм². Можно ли считать, что внесение удобрений привело к значимому росту растений (гипотеза H₁), или различие и обусловлено случайными причинами (гипотеза H₀)?

У к а з а н и е: предварительно проверить нулевую гипотезу о равенстве генеральных дисперсий H₀: D(X) = D(Y) при конкурирующей гипотезе H₁: D(X)  D(Y).

22. Физическая подготовка n = 9 спортсменов была проверена при поступлении в спортивную школу (с.в. X), а затем после недели тренировок (с.в. Y). Итоги проверки (в баллах) оказались следующими:

xi	76	71	57	49	70	69	26	65	59
yi	81	85	52	52	70	63	33	83	62

В предположении, что обе с.в. распределены нормально, проверить, значимо или незначимо улучшилась физическая подготовка спортсменов? Гипотеза H₀: M(X) = M(Y). Гипотеза H₁: M(X) < M(Y).

23. Измерения отклонения (в мкм) от проектного размера (с.в. X) для случайной выборки из n = 200 изделий следующие результаты:

xi	0,3	0,5	0,7	0,9	1,1	1,3	1,5	1,7	1,9	2,1	2,3	Прим.
ni	6	9	26	25	30	26	21	24	20	8	5	Sni = 200

Гипотеза H₀: с.в. X имеет нормальное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от нормального.

24. Установить, значимо или незначимо различаются эмпирические (n_i) и теоретические (n_i¢) частоты, вычисленные в предположении о нормальности распределения для случайной выборки из n = 200 испытаний:

ni	6	8	13	15	20	16	10	7	5	Прим.
ni¢	5	9	14	16	18	16	9	6	7	Sni = 100

Гипотеза H₀: с.в. X имеет нормальное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от нормального.

25. С.в. X из n = 100 наблюдений задана интервальным частотным вариационным рядом. Можно ли утверждать, что генеральная совокупность распределена по нормальному закону?

xi	3 ¸ 8	8 ¸ 13	13 ¸ 18	18 ¸ 23	23 ¸ 28	28 ¸ 33	33 ¸ 38	Прим.
ni	6	8	15	40	16	8	7	Sni = 100

Гипотеза H₀: с.в. X имеет нормальное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от нормального.

26. По техническим условиям средняя прочность на разрыв троса составляет 2000 кг. В результате испытаний 20 кусков троса было установлено, что средняя прочность на разрыв равна 1955 кг, а выборочная исправленная дисперсия равна 625 кг². Удовлетворяет ли образец троса техническим условиям (гипотеза H₀), или наблюдаемое отклонение неслучайно (гипотеза H₁)?

27. С.в. X из n = 300 наблюдений задана интервальным частотным вариационным рядом. Можно ли утверждать, что генеральная совокупность распределена по нормальному закону?

xi	–20 ¸ –10	–10 ¸ 0	0 ¸ 10	10 ¸ 20	20 ¸ 30	30 ¸ 40	40 ¸ 50	Прим.
ni	20	47	80	89	40	16	8	Sni = 300

Гипотеза H₀: с.в. X имеет нормальное распределение.

Гипотеза H₁: с.в. X имеет распределение, отличное от нормального.

28. Опыт, состоящий в одновременном подбрасывании четырех монет, повторили n = 100 раз. Эмпирическое частотное распределение с.в. X, – числа выпадений «гербов», есть:

xi	0	1	2	3	4	Прим.
ni	8	20	42	22	8	Sni = 100

Гипотеза H₀: с.в. X распределена по биномиальному закону.

Гипотеза H₁: с.в. X имеет распределение, отличное от биномиального.

29. Проектный контролируемый размер изделий (в мм), изготавливаемых станком - автоматом, a = a₀ = 30 мм. Измерения n = 30 случайно отобранных изделий дали следующие результаты:

xi	29,6	29,7	29,8	29,9	30,0	30,1	30,2	30,3	30,4	Прим.
ni	2	3	4	5	6	5	3	1	1	Sni = 30

Обеспечивает ли станок изготовление деталей в проектном размере?

Гипотеза H₀: a = a₀ = 30 мм. Гипотеза H₁: a < a₀.

30. Ежемесячная производительность двух моторных заводов X и Y, выпускающих дизельные двигатели, характеризуется следующими данными за первые 10 мес. года:

xi	72	84	69	74	82	67	75	86	68	61
yi	55	65	73	66	58	71	77	68	68	59

Можно ли считать одинаковыми средние производительности дизельных двигателей на обоих заводах (гипотеза H₀), или их различие статистически значимо (гипотеза H₁)?

ИДЗ-10. Элементы корреляционного анализа

Найти коэффициент линейной корреляции Пирсона и уравнение линии регрессии между количественно измеряемыми с.в. X и Y, либо найти выборочные коэффициенты ранговой корреляции (Спирмена или Кендалла) между с.в. A и B, ранжированными в порядковой шкале. Используя подходящий статистический критерий, проверить гипотезу о значимости найденного коэффициента корреляции. Уровень значимости  = 0,05.

У к а з а н и е. Рекомендуется использование математического программного обеспечения для проведения расчетов и представления результатов в табличном (графическом) виде.

1. Знания n = 10 студентов проверены по двум тестам A и B. Оценки по стобалльной системе оказались следующими:

A	95	90	86	84	75	70	62	60	57	50
B	92	93	83	80	55	60	45	72	62	70

Вычислив коэффициент ранговой корреляции Спирмена, установить согласуются ли результаты испытаний по тестам A и B?

2. Для исследования корреляционной связи между ценой X и спросом Y на некоторый товар провели статистическое наблюдение в нескольких торговых точках фирмы. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице:

Цена товара, руб.	125	140	115	110	165	130	145	105	120	135
Число покупок	153	95	160	110	64	120	92	107	140	102

Существует ли значимая линейная корреляционная связь между случайными величинами X и Y?

3. Два контролера расположили десять деталей в порядке ухудшения их качества. В итоге были получены две последовательности рангов A и B:

A	1	2	3	4	5	6	7	8	9	10
B	1	2	4	3	6	5	7	10	9	8

Используя коэффициент ранговой корреляции Кендалла определить, согласуются ли оценки контролеров.

4. Для исследования корреляционной связи между посещаемостью занятий X и результатами экзамена Y (в 10-балльной системе) по математике деканат математического факультета вуза провел выборочный статистический анализ в одной из студенческих групп:

Ф.И.	АЕ	БВ	БЕ	ДЛ	ЕК	ЖЮ	КЮ	ЛА	НЗ	НА	ПЕ	ПЛ	СН
X, %	59	47	100	82	77	47	82	100	41	47	71	35	94
Y, б.	6	7	9	8	8	7	5	7	5	5	6	4	7

Можно ли утверждать на основании этих данных, что высокая посещаемость занятий в семестре является залогом получения хорошей экзаменационной оценки?