
ИДЗ Математика ИКРиМ 1 семестр v2
.docили
ln x = x2.
Это уравнение не имеет действительных корней. Для того, чтобы убедиться в этом, достаточно сопоставить два графика элементарных функций y = ln x и y = x2.
3. Функция f(x) не является четной или нечетной, не является периодической, т.е. является функцией общего вида.
4. Для исследования функции на монотонность и экстремум вычислим ее первую производную:
y
= (![]() – x)
=
– x)
= ![]() – 1 =
– 1 = ![]() – 1 =
– 1 = ![]() .
.
Особыми точками являются: точка x0 = 0 (при x 0 производная функции y(x) +) и точка x1 = 1 (здесь y(x) = 0). В первом случае, очевидно, имеем вертикальную асимптоту x = 0 для графика функции y(x). Во втором случае, как нетрудно видеть, сравнив графики элементарных функций y = ln x и y = 1 – x2, уравнение
ln x = 1 – x2
имеет единственным корнем именно x1 = 1. Заметим, что при x < 1 ln x < 1 – x2, а при x > 1 ln x > 1 – x2.
Особые точки делят область определения функции D на два (непересекающихся) интервала: D1 = (0; 1) и D2 = (1; +). Изучим каждый из них.
Интервал D1 = (0; 1). Здесь y > 0 и функция y = f(x) возрастает.
Интервал D2 = (1; +). Здесь y < 0 и функция y = f(x) убывает.
Знак первой производной y(x) изменяется c «+» на «–» в точке x1 = 1; в этой точке функция y = f(x) достигает (локального) максимума, равного ymax = f(1) = –1.
5. Для определения интервалов выпуклости и вогнутости и точек перегиба вычислим вторую производную функции, как производную отношения:
y
= (
![]() – 1)
=
– 1)
= ![]() =
= ![]() .
.
Точками, подозрительными на перегиб (там, где вторая производная y(x) равна нулю или не существует) являются точки x0 = 0 и x2 = e3/2 4,482.
В области 0 < x < x2 вторая производная y < 0 и функция y = f(x) выпукла вверх (выпукла). В области x2 < x < + вторая производная y > 0 и функция y = f(x) выпукла вниз (вогнута). Так как в точке x2 = e3/2 4,482 вторая производная y меняет знак с «–» на «+», то точка x2 является точкой перегиба.
6. Найдем наклонные (горизонтальные) асимптоты y = kx + b графика функции. В данном случае, применяя правило Лопиталя, находим
k = ![]() =
= ![]() = – 1 +
= – 1 + ![]() = –1,
= –1,
действительно, ![]() =
= ![]() =
= ![]() = 0.
= 0.
b = ![]() =
= ![]() =
= ![]() =
= ![]() = 0.
= 0.
Таким образом, график y(x) исследуемой функции имеет единственную наклонную асимптоту y = –x.
7. Необходимости в дополнительных
вычислениях для уточнения поведения
графика функции y(x)
нет. Можно, однако, заметить дополнительно,
что разность между значениями исследуемой
функции y(x)
= ![]() – x и соответствующими
асимптотическими значениями y
= –x всегда положительна:
y(x)
=
– x и соответствующими
асимптотическими значениями y
= –x всегда положительна:
y(x)
= ![]() – x – (–x)
=
– x – (–x)
= ![]() > 0 при x > 0. Поэтому
функция y = f(x)
приближается к своей асимптоте сверху.
> 0 при x > 0. Поэтому
функция y = f(x)
приближается к своей асимптоте сверху.
8. Объединяя результаты проведенных выше исследований, строим график функции y = f(x) (рис. 3).

Рис. 3
ИДЗ-12. Решение задачи оптимизации.
Построить математическую модель и решить задачу оптимизации.
Среди всех равнобедренных треугольников с заданным периметром p найти треугольник наибольшей площади. Чему она равна?
Р A
 необходимые
обозначения в рассматриваемом треугольнике
ABC:
AB = AC
= x; BC
= y; AD
= xcos;
A
= 2. Заданный периметр
p = 2x
+ y.
необходимые
обозначения в рассматриваемом треугольнике
ABC:
AB = AC
= x; BC
= y; AD
= xcos;
A
= 2. Заданный периметр
p = 2x
+ y.

 Из
геометрических соображений имеем:
Из
геометрических соображений имеем:
p = 2x + 2x sin = 2x (1 + sin ),
о
B C D
x = ![]()
![]() .
.
Рис. 4
S = ![]() BCAD
=
BCAD
= ![]() 2x
sin
x
cos
=
2x
sin
x
cos
= ![]() x2
sin 2
=
x2
sin 2
= ![]()
![]() .
.
Ясно, что 0
![]() .
Остается найти максимальное значение
целевой функции:
.
Остается найти максимальное значение
целевой функции:
f()
= ![]() .
.
Для этого вычислим производную функции f() и приравняем ее нулю:
f()
= 0 = (![]() )
=
)
= ![]() = 2
= 2![]() =
=
= 2![]() = 2
= 2![]() = 2
= 2![]() .
.
При допустимых значениях угла выражение 1 + sin > 0, так что f() = 0 при
cos 2 – sin = 0;
1 – 2sin2 – sin = 0;
2sin2 + sin – 1 = 0;
D = 12 – 42(–1) = 9;
sin
= ![]() =
= ![]() ;
;
Допустимым значениям угла
отвечает лишь решение sin
= ½, откуда 0
= ![]() и A
=
и A
= ![]() .
Тогда y = 2x
.
Тогда y = 2x![]() = x, т.е. ABC
равносторонний.
= x, т.е. ABC
равносторонний.
Нетрудно (СРС) вычислить вторую производную целевой функции f():
f()
= (2![]() )
= –2
)
= –2![]() .
.
При найденном значении m
= ![]() вторая производная f(0)
< 0, т.е. в точке m
=
вторая производная f(0)
< 0, т.е. в точке m
= ![]() площадь S()
достигает именно максимума, равного
площадь S()
достигает именно максимума, равного
Sm
= S(![]() )
=
)
= ![]()
![]() =
= ![]()
![]() =
= ![]() .
.
Ответ: m
= ![]() ;
Sm
=
;
Sm
= ![]() .
.
Варианты индивидуальных домашних заданий (ИДЗ) по Математике
ИДЗ-1. Действия с определителями
Для данного определителя : а) найти алгебраические дополнения элементов 1-ой строки и 1-го столбца; б) вычислить определитель , приведя его к треугольному виду, или получив предварительно нули в к.-л. строке или столбце; в) проверить расчет, применяя разложение определителя по элементам 1-ой строки или 1-го столбца и используя алгебраические дополнения соответствующих элементов из задания а).
-
 . 2.
. 2.
 . 3.
. 3.
 .
.
4.  . 5.
. 5.
 . 6.
. 6.
 .
.
7.  . 8.
. 8.
 . 9.
. 9.
 .
.
10.  . 11.
. 11.
 . 12.
. 12.
 .
.
13.  . 14.
. 14.
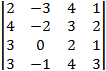 . 15.
. 15.
 .
.
16.  . 17.
. 17.
 . 18.
. 18.
 .
.
19.  . 20.
. 20.
 . 21.
. 21.
 .
.
22.  . 23.
. 23.
 . 24.
. 24.
 .
.
25.  . 26.
. 26.
 . 27.
. 27.
 .
.
28.  . 29.
. 29.
 . 30.
. 30.
 .
.
ИДЗ-2. Действия с матрицами
Даны две матрицы A и B. Найти: а) AB; б) BA; в) A–1; г) AA–1; д) A–1A.
-
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
= 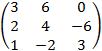 .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
= 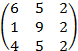 .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
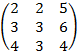 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
= 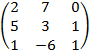 .
. -
A =
 ; B
=
; B
= 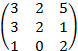 .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
. -
A =
 ; B
=
; B
=  .
.
ИДЗ-3. Решение неоднородной системы линейных алгебраических уравнений
Проверить совместность системы уравнений и в случае совместности решить ее: а) по правилам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса.
1.  2.
2.

3.  4.
4.

5.  6.
6.

7.  8.
8.

9.  10.
10.

11.  12.
12.

13.  14.
14.

15.  16.
16.
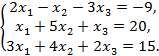
17.  18.
18.

19.  20.
20.

21.  22.
22.

23.  24.
24.

25.  26.
26.

27.  28.
28.
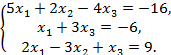
29.  30.
30.

ИДЗ-4. Решение однородной системы линейных алгебраических уравнений
Решить однородную систему линейных алгебраических уравнений.
1.  2.
2.

3.  4.
4.

5.  6.
6.
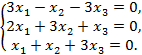
7.  8.
8.

9.  10.
10.

11.  12.
12. 
13.  14.
14.

15.  16.
16.

17.  18.
18.

19.  20.
20.

21.  22.
22.

23.  24.
24.

25.  26.
26.

27.  28.
28.

29.  30.
30.
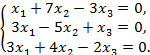
ИДЗ-5. Вычисление пределов с использованием теорем о пределах
Вычислить пределы, применяя теоремы о пределах.
-
 ;
;  ;
;  .
. -
 ;
; 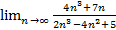 ;
;  .
. -
 ;
; 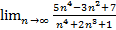 ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
; 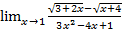 .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
; 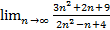 ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
; 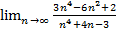 ;
; 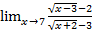 .
. -
 ;
;  ;
; 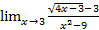 .
. -
 ;
; 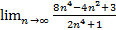 ;
; 
-
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
; 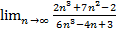 ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
. -
 ;
;  ;
;  .
.
