Касательная плоскость и нормаль к поверхности

Пусть M₀(x₀; y₀; z₀) – фиксированная точка на поверхности, заданной функцией z = f(x; y) или уравнением F(x; y; z) = 0.

Касательной плоскостью к поверхности в точке M₀ называется плоскость, в которой расположены касательные к всевозможным кривым, проведенным на поверхности через точку M₀.

Нормалью называется прямая, проходящая через точку M₀ перпендикулярно касательной плоскости.

Из определений следует, что нормальный вектор касательной плоскости и направляющий вектор нормали совпадают.

Если поверхность задана уравнением z = f(x; y), то уравнение касательной плоскости в точке M₀(x₀; y₀; z₀) к данной поверхности имеет вид

(1)

а канонические уравнения нормали, проведенной через точку M₀(x₀; y₀; z₀) поверхности, имеют вид

(2)

В случае, когда уравнение гладкой поверхности задано в неявном виде: F(x; y; z) = 0 и F(x₀; y₀; z₀) = 0, то уравнение касательной плоскости в точке M₀(x₀; y₀; z₀) имеет вид

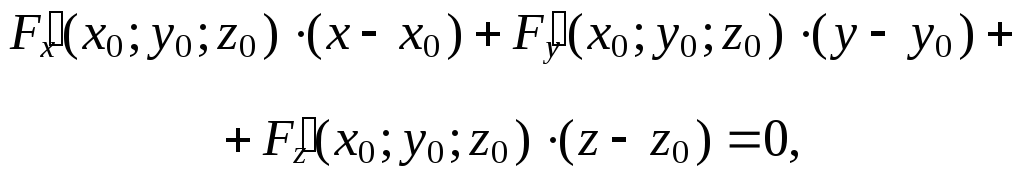(3)

а уравнение нормали

(4)

Пример 15.Найти уравнение касательной плоскости и уравнения нормали к поверхностив точкеM₀(1; 2; –1).

Решение

Вычисляем значения частных производных в точке M₀(1; 2; –1)

Подставляя их в уравнения (3) и (4), получаем соответственно уравнение касательной плоскости: канонические уравнения нормали:

Тест 11. Уравнение касательной плоскости к поверхности в точкеP₀(2; –3; 2) имеет следующий вид:

1)

2)

3)

4)

5)

Производная по направлению. Градиент

Частные производные ипредставляют собой производные от функцииz = f(x; y) по двум частным направлениям осей Ox и Oy (рисунок 43).

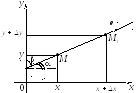
Рисунок 43

Пусть функция z = f(x; y) определена в некоторой окрестности точки М(х; у), – некоторое направление, задаваемое единичным векторомгдеибо(или);cos , cos  – косинусы углов, образуемых вектором е с осями координат и называемые направляющими косинусами.

При перемещении в данном направлении точкиM(x; y) в точку M₁(x + x; y + y) функция z получит приращение z = f(x + x; y + + y) – f(x; y), называемое приращением функции в данном направлении

Если то, очевидно, чтоследовательно,

Производной по направлению функции двух переменных z = f(x; y) называется предел отношения приращения функции в этом направлении к величине перемещения при стремлении последней к нулю, т. е.

Производная характеризует скорость изменения функции в направлении

Формула для производной функции z = f(x; y) по направлению имеет вид

Пример 16. Дана функция z = x² + y², в точке M(1; 1) направление составляет с осью Ox угол Найти производную функции по указанному направлению в этой точке.

Решение

Так как то уголПо формуле производной функции по направлению получим

В точке M(1; 1) получаем:

Градиентом grad z функции z = f(x; y) называется вектор с координатами

Рассмотрим скалярное произведение векторов и единичного вектора

Получим

Итак, производная по направлению есть скалярное произведение градиента grad z и единичного вектора, задающего направление

Градиент функции grad z в данной точке характеризует направление максимальной скорости изменения функции в этой точке.

Пример 17. Найти градиент функции в точкеM(0; 1).