Решение

Чтобы найти f(1; 2), надо в выражении для f(x; y) подставить x = 1, y = 2 и выполнить указанные в f действия.

Имеем:

Пример 2. Найти область определения функции и изобразить графически.

Решение

Эта функция двух переменных определена, когда выражение под знаком квадратного корня неотрицательно, т. е. 4 – х² – y²  0 или x² + y²  4. Последнему соотношению удовлетворяют координаты всех точек, находящихся внутри круга радиусом R = 2 с центром в начале координат и на его границе. Область определения данной функции – указанный круг (рисунок 40).

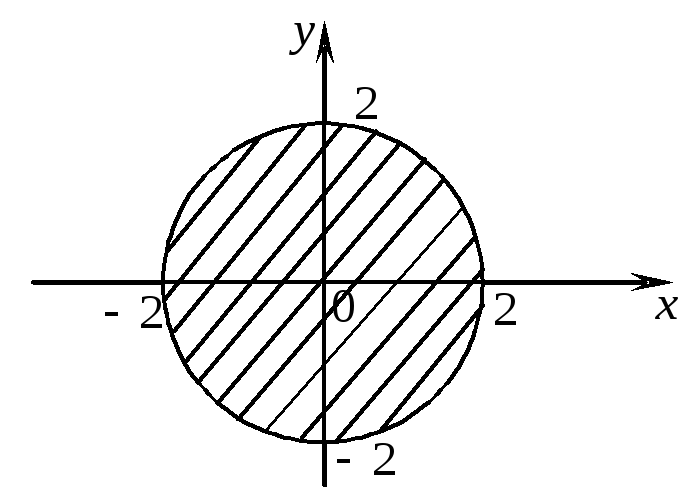
Рисунок 40

Пример 3.Найти область определения функциии изобразить графически.

Решение

Данная функция определена на интервале [–1; 1], т. е.

или

Неравенства y²  x и y²  –x задают часть плоскости, расположенную вне обеих парабол одновременно. Отметим, что точка (0; 0) не входит в искомую область определения.

Найденное множество точек, являющееся областью определения заданной функции, штриховкой показано на рисунке 41.

Рисунок 41

Пример 4. Найти область определения функции и изобразить графически.

Решение

Область определения функции находится как решение неравенства

или

Это неравенство описывает внутреннюю часть эллипса (рисунок 42).

Рисунок 42

Тест 1. Значение функции f(x)в точке (2; 1) равно:

1) 7;

2) –5;

3) –1;

4) 1;

5) –2.

Тест 2. Область определения функции является:

1)

2)

3)

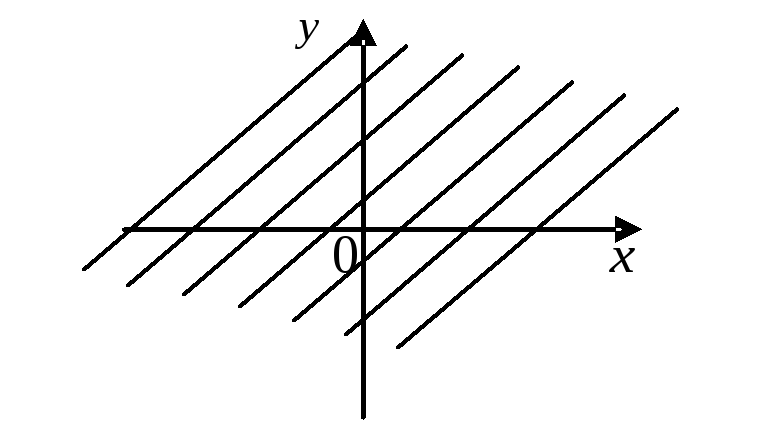
4)

5)

Тест 3. Указать функцию двух переменных:

1)

2)

3)

4)

5)

Предел функции

Число называетсяпределом функции z = f(x; y) в точке M₀(x₀; y₀), если для любого числа  > 0 найдется число  > 0, зависящее от , такое, что для всех точек M(x; y), отстоящих от M₀ не более чем на , выполняется неравенство

Записывают:

На функции нескольких переменных легко переносятся все положения теории пределов функции одной переменной, в частности, справедлива теорема, представленная ниже.

Теорема

1)

2)

3) 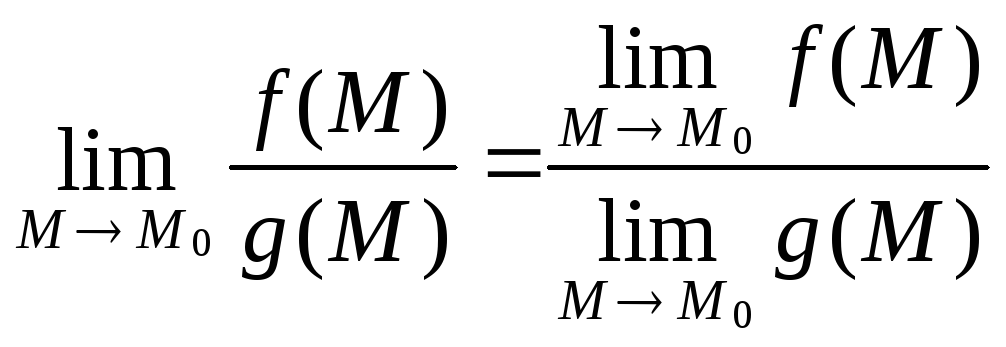,если

Пример 5. Найти предел

Решение

Пример 6. Найти предел

Решение

Имеем неопределенность вида Раскроем эту неопределенность. Избавимся от иррациональности в числителе

Пример 7. Вычислить

Решение

Имеем неопределенность вида Находим

так как

Пример 8. Вычислить

Решение

Имеем неопределенность вида Выражение, стоящее под знаком предела, преобразуем к такому виду, чтобы можно было воспользоваться вторым замечательным пределом

Пример 9. Вычислить

Решение

Данная функция определена всюду на координатной плоскостиOxy, кроме точки O(0; 0). Рассмотрим предел этой функции при стремлении точки M(x; y) к началу координат по любой прямой, проходящей через точку O, т. е. вдоль линии (k  0)

Получили, что значение предела зависит от углового коэффициента прямой. Итак, соответствующим разным значениям k получаем разные предельные значения. Отсюда следует, что предел данной функции в точке O(0; 0) не существует.

Тест 4. Вычислить предел (4ху – 1):

1) –3;

2) 0;

3) –8;

4) –9;

5) –10.

Тест 5. Вычислить

1) ;

2) 0;

3) 2;

4) 5;

5) .

Непрерывность функции двух переменных

Функция z = f(x; y) называется непрерывной в точке (x₀; y₀), если она:

1) определена в точке (x₀; y₀);

2) имеет конечный предел при x  x₀ и y  y₀;

3) этот предел равен значению функции в точке (x₀; y₀), т. е.

Геометрический смыслнепрерывности заключается в том, что график в точке (x₀;y₀) представляет собой сплошную нерасслаивающуюся поверхность.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в данной области.

Если в некоторой точке N(x;y) не выполняется условие непрерывности, то эта точка называетсяточкой разрыва функцииz=f(x;y).

Нарушение условий непрерывности функции z=f(x;y) может происходить как в отдельных точках, так и в точках, образующих некоторую линию (линия разрыва).

Пример 10. Найти точки разрыва функций:

1)

2)

3)

Решение

1. Данная функция определена для любых x,y, таких, чтох–у0,т. е. х  у. Следовательно, прямая x = y является линией разрывафункции.

2. Данная функция определена на R²всюду, кроме точки (5; 0), которая и является точкой разрыва функции.

3. Функция определена для любыхx,y,z, таких, чтоСфера с центром в начале координат и радиусом 4 является поверхностью разрыва функции.

Тест 6. Функция не является непрерывной в точке:

1) (0; 0);

2) (2; 1);

3) (0; 1);

4) (8; 0);

5) (1; 2).