Дифференциал функции

Дифференциалом функции y = f(x) в точке называется главная частьее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy или или dy = f (x)dx, так как dx = x. Из второй формулы следует, что

При достаточно малых справедлива приближенная формула

или

Данная формула часто используется в приближенных вычислениях.

Пример 11. Найти дифференциал функции

Решение

По формуле находим

Тест 6. Дифференциал функции равен:

1)

2)

3)

4)

5)

Пример 12. Найти дифференциал функции y = x² + 2x + 2 в точке x = 1.

Решение

По формуле находим

Подставим x = 1 в dy и получим

Тест 7. Дифференциал dy функции в точкеx = 3 равен:

1)

2)

3) ln 6 dx;

4)

5)

Пример 13. Найти приближенное значение

Решение

Нам известно значение равноеВоспользуемся им и формулойВ качествеследует взять радианную мерут. е. величинусо знаком «минус». Имеем

х = –

Поэтому получаем, что

Ответы на тестовые задания

Номер теста	1	2	3	4	5	6	7
Правильный ответ	5	3	2	1	5	5	1

2.5. Основные теоремы о дифференцируемых функциях Теорема Ферма

Теорема. Пусть функция y = f(x) определена в интервале (а; b) и в некоторой точке c  (а; b) принимает наибольшее (наименьшее) значение. Тогда, если в точке существует производная, то она равна нулю:

Геометрический смысл теоремы: так как то касательная к графику функции в точкеМ, абсцисса которой равна с, параллельна оси Ox (рисунок 29).

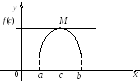
Рисунок 29

Замечания:

1. По условию теоремы функция определена в интервале (a; b). В этом промежутке все точки внутренние. Таким образом, точка взята внутри промежутка Х.

2. Если функция принимает наибольшее (наименьшее) значение на конце промежутка, например, в точке а промежутка X = [a; b], и в этой точке существует конечная односторонняя производная, то она может не равняться нулю.

Пример 1. Проверить, удовлетворяет ли функция условиям теоремы Ферма на отрезке

Решение

Функция определена на интервале

На концах отрезка функция принимает наибольшее и наименьшее значения: при х = 0 функция принимает наименьшее значение: f(0) = 0² = 0; при – наибольшее значение:

Условие теоремы не выполнено, поскольку наибольшее (наименьшее) значение функция должна принимать внутри промежутка, а не на его концах.

В результате, хотя функция в точке принимает наибольшее значение и имеет конечную производную:производная в этой точке отлична от нуля:

Пример 2. Проверить, удовлетворяет ли функция у = х² условиям теоремы Ферма на отрезке

Решение

Функция определена на интервале

При х = 0 функция принимает наименьшее значение: f(0) = 0² = 0. Это наименьшее значение функция принимает внутри интервала.

Функция у = х² в точке х = 0 имеет конечную производную: которая в этой точке равна нулю:

Таким образом, теорема Ферма применима к функции у = х² на отрезке

Тест 1. Пусть функция y = f(x) определена в интервале (a; b) и в некоторой точке c  (а; b) принимает наибольшее (наименьшее) значение. Тогда, если в точке существует производная, то:

1) 

2)

3)

4)

5)

Тест 2. Теорема Ферма применима, если:

1) функция y = f(x) определена в интервале (a; b);

2) функция y = f(x) в некоторой точке c Î (а; b) принимает наибольшее (наименьшее) значение;

3) функция y = f(x) определена в интервале (a; b) и в некоторой точке c Î (а; b) принимает наибольшее (наименьшее) значение;

4) функция y = f(x) определена в интервале (a; b) и в некоторой точке c Î (а; b) принимает наибольшее (наименьшее) значение, причем, в точке существует конечная производная

5) в точке c Î (а; b) существует конечная производная

Тест 3. Условиям теоремы Ферма на отрезке удовлетворяет функция:

1)

2)

3)

4)

5)