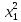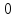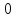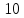5.7. Матричный подход к регрессионному анализу.

Многие сложные случаи, возникающие при планировании эксперимента, требуют матричной формы описания. Для её рассмотрения целесообразно вернуться к изложенному ранее методу наименьших квадратов.

1. Метод наименьших квадратов.

Рассмотрим численный пример линейного уравнения для одного фактора, а затем его описание на языке матриц. Численные значения опыта представлены в таблице 19.

Таблица 19

Номер опыта	x1	y
1 2 3 4 5	-2 -1 0 +1 +2	0 1 2 3 4

Допустим, известно, что y связан с x₁ линейным уравнением

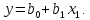
Произведем вычисления в соответствии с ранее приведенной таблицей 17.

Таблица 20

Номер опыта	x1	y		y x1	y2	x1+y	(x1+y)2
1 2 3 4 5 ∑ Среднее значение	-2 -1 0 +1 +2	0 1 2 3 4 2	0 4	0 -1 0 3 8.	4 16	-2 0 2 4 6 --	4 0 4 16 36

Воспользовавшись формулами ( 19 и 20) получим результат

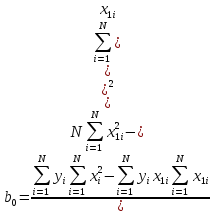
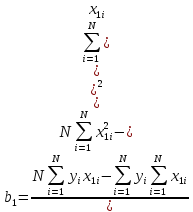
Теперь можно написать уравнение y = 2 + 1 x₁.

С помощью данного примера воспроизведена процедура МТК.

Рассмотрим этот же пример на языке матриц. В этом примере участвуют три множества элементов: элементы задающие условия проведения опытов, элементы, характеризующие их результаты, и неизвестные коэффициенты, которые нужно определить.

Так, элементы, характеризующие результаты опытов, можно представить в виде столбца

неизвестным коэффициентам соответствует столбец

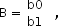
а элементы, задающие условия опытов удобно представить в виде таблицы

В этой таблице появился столбец х₀, состоящий из +1. Он введен для удобства вычислений всех коэффициентов, включая свободный член b_о. Фактически это значит, что исходное уравнение приняло вид: у=b_ох₍₎+b₁х₁.

Таблицы, в которых собраны упорядоченные некоторым обра­зом элементы, называются матрицами. Следовательно, в нашем случае Y, В и X являются матрицами. Элементы Y упорядочены по номерам опытов, элементы X, кроме того, — по номерам пе­ременных (х₀, х₁), а элементы В — по номерам коэффициентов, которые соответствуют номерам переменных.

Для того чтобы воспользоваться матрицами при описании регрессионного анализа, необходимо ввести некоторые операции над ними.

5.7.2. Некоторые операции над матрицами

Матрицы, описанные в предыдущем параграфе, различаются по числу элементов, числу строк и числу столбцов. Так, в матрице У один столбец, пять строк и пять элементов, а в матрице X тоже пять строк, но два столбца и десять элементов. Если число строк и число столбцов различны, то матрицы назы­ваются прямоугольными, а при равном числе строк и столб­цов — квадратными. Все матрицы из этого примера —

прямоугольные. Если матрица имеет всего один столбец, то ее называют матрицей-столбцом или вектор-столбцом. Примерами служат матрицы Y и В. Аналогично можно определить и матрицы-строки (векторы-строки).

В приведенном примере матрцы представляют систему из пяти следующих уравнений по одному уравне­нию для каждого опыта:

у_i = b₀ x₀+b₁x_1i ( i=1,2,….,5) или в развернутом виде:

0 = b₀∙ 1+ b₁ ∙ (-2);

1 = b₀∙ 1+ b₁ ∙ (-1);

2 = b₀∙ 1+ b₁ ∙ (-1);

3 = b₀∙ 1+ b₁ ∙ (+1);

4 = b₀∙ 1+ b₁ ∙ (+2).

На матричном языке эта система уравнений выглядит следующим образом:

Y=XB, т.е.

Чтобы эти две записи стали эквивалентными, необходимо ввести определенные правила перемножения матриц. Будем в произведении различать матрицу, стоящую слева, и матрицу, стоящую справа. Перемножить две матрицы это значит получить матрицу произведений, элементы которой находятся по следую­щим правилам.

Элементы первой строки матрицы, стоящей слева, умножаются на соответствующие элементы матрицы, стоящей справа, и полу­ченные произведения складываются. В нашем случае имеем: (+1) b₀+(—2)b₁. Для получения элемента, стоящего на пересе­чении первого столбца и второй строки, аналогичная операция проделывается со второй строкой матрицы, стоящей слева, и тем же самым первым столбцом матрицы, стоящей справа, т. е. (+1) b₀+(—1) b₁. Продолжая таким образом до последней строки матрицы, стоящей слева, получаем все элементы первого столбца матрицы произведений. Эта процедура повторяется столько раз, сколько вектор-столбцов содержит матрица, стоящая справа. В нашем случае эта матрица имеет только один столбец. Из опре­деления видно, что матрица произведений имеет столько столб­цов, сколько матрица, стоящая справа, и столько строк, сколько матрица, стоящая слева. В рассматриваемом примере матрица-произведение имеет один столбец и пять строк, что соответствует размерности матрицы Y. И тогда матрица-произведение имеет вид

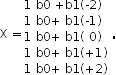
( 21)

Сопоставление матрицы-произведения с системой уравнений убеждает нас в тождественности матричной и нематричной форм записей. Вектор У, оказывается, и есть матрица произведений в данном случае. Элементы матрицы-произведения называются скалярными произведениями вектор-строки матрицы, стоящей слева, и соответствующего вектор-столбца матрицы, стоящей справа. В правилах перемножения матриц существуют особенности, не имеющие аналога в числах. Так, небезразлично, в каком по­рядке записаны матрицы в произведении. Левая и правая матрицы неравноправны. Если умножить матрицу В на матрицу X (ВХ), то этого сделать невозможно, ибо длины векторов, входящих в скалярное произведение, должны быть согласованы.

Таким образом, для двух произвольных матриц произведение су­ществует, если число столбцов матрицы, стоящей слева, равно числу строк матрицы, стоящей справа. Ясно, что для двух квадратных мат­риц одинакового размера существуют оба произведения (справа и слева), однако они могут быть различными. Матрицы, произведение которых не зависит от порядка сомножителей, называются комму­тирующими. В общем же случае для произведения матриц комму­тативный закон не выполняется.

Перейдем теперь к системе нормальных уравнений МНК, которая в соответствии с 18 и 19 выглядит следующим образом.

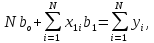
5b₀ + 0b₁ = 10 ,

0b₀ +10b₁ = 10 .

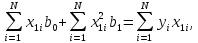
Можно показать, что в матричном виде она запишется следующим образом: X^TXB=X^TY. Здесь Х^Т обозначает матрицу, транспо­нированную по отношению к матрице X. Протранспонировать матрицу— это значит столбцы исходной матрицы сделать строками транспонированной матрицы, сохранив их последовательность. Так. в нашем случае транспонированная матрица имеет вид:

Для получения системы нормальных уравнений пришлось умножить обе части исходной системы уравнений слева на Х^т.

Покажем, как выполняются эти операции.

+1 +1 +1 +1 +1

Х^ТX =

-2 -1 0 +1 +2

+1 0

+1 1

+1 2

+1 3

+1 4

∙

=

;

=

5 0

0 10

=

+1 +1+1+1+1 -2 -1 0+1 +2

-2 -1 0+1+2+4+1 0+1 +4

Теперь можно записать систему уравнений

∙= .

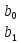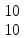Из неё следует 5b₀ + 0b₁ = 10 и 0b₀ +10b₁ = 10 . Эти уравнения и были приняты как исходные.

Матрица Х^ТХ называется матрицей системы нормальных уравнений. Она обладает рядом важных для нас свойств. В этой матрице два элемента, расположенных симметрично относительно диагонали, идущей с левого верхнего угла в правый нижний (так называемой главной диагонали), равны между собой. В рассматриваемом случае это нули. Такое свойство характерно для матриц систем нормальных уравнений МНК, так как векторы, входящие в скалярные произведения, комму­тативны.

Матрица, элементы которой симметричны относительно глав­ной диагонали, называется симметричной. Если все элементы вне главной диагонали равны нулю, то такая матрица называется диагональной. В дальнейшем нам понадобится еще одна разновид­ность диагональных матриц. Диагональная матрица, все элементы главной диагонали которой являются единицами, называется еди­ничной матрицей. Единичная матрица играет в алгебре матриц такую же роль как единица в алгебре чисел.

Решить систему нормальных уравнений это значит записать в явном виде элементы вектора В (b₀ и b₁). Если бы мы имели дело с числами, то для этого нужно было бы поделить обе части на коэф­фициент при неизвестном и получить ответ. Но для матриц вместо деления (которое не определено) используется специальная операция умножения на обратную матрицу.

2. Обобщение метода наименьших квадратов на многофакторный линейный случай

Пусть имеется k факторов и известно, что отклик и факторы связаны линейно: y = b₀x₀ + b₁x₁ + b₂x₂ +…..+ b_kx_k. Выпишем для этого случая матрицы X, Y, B.

∙

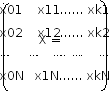
Матрица X прямоугольная, содержащая k+1 столбец и Nстрок.

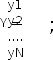
- результаты опыта

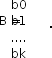
-коэффициенты полинома.

Домножим левую и правую часть уравнения на одну и ту же матрицу X^T – транспонированную матрицу Х

X^TY = X^TXB.

Транспонированная матрица – это матрица, у которой по отношению к исходной столбцы и строки поменяны местами:

Матрица С =X^ТХ является квадратной, содержащей k = 1 строк и k = 1 столбцов.

Заменим в выражении X^TY = X^TXB произведение X^TX на С и определим В : B = C^-1X^тY.

В качестве примера рассмотрим полином y_k = b₀x₀ + b₁x_k ,

x₀= 1, k = 1,..... N, формируемый по результатам N опытов.

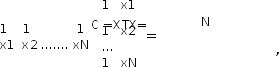
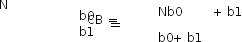
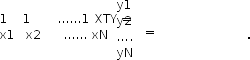
CB = X^ТY.

Nb₀ + b₁ =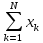

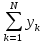
b₀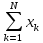+ b₁ =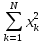

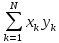
Эти соотношения полностью совпадают с соотношениями для такого же полинома при использовании МТК.