5.4.3. Эмпирические (выборочные) моменты

Эмпирическая функция распределения содержит всю ста­тистическую информацию, которая накоплена в процессе из­влечения выборки. Статистические свойства выборки можно характеризовать не только такой функцией, но и более гру­бо — выборочными моментами, которые будем обозначать звездочкой в отличие от моментов случайных величин.

Выборочный момент к-го порядка

( 11 )

( 12 )

( 13 )

т.е. он равен среднему арифметическому k-x степеней выбо­рочных значений.

Выборочный момент первого порядка называется выбо­рочным средним

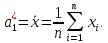
Выборочные моменты k-ro порядка служат оценкой мо­ментов k-го порядка случайной величины X.

Аналогично оценкой k-ro центрального момента

а_к == М(Х-МХ)^к служат выборочные моменты

В случае k=2 получаем выборочную дисперсию

( 14 )

Выборочное среднее характеризует расположение выбор­ки на действительной прямой, а выборочная дисперсия явля­ется мерой рассеяния выборочных значений относительно среднего.

Можно показать, что при достаточно общих ограничени­ях, налагаемых на неизвестную функцию распределения F(x), выборочные моменты близки к ее соответствующим теорети­ческим характеристикам

а_к = МХ^к; = М(Х-МХ)^к.

5.5. Теория точечных оценок

Несмещенные оценки с минимальной дисперсией

Предположим, что о распределении случайной величины X известно, что оно принадлежит некоторому параметрическому семейству распределений. В случае непрерывной случайной величины это означает, что известен вид плотности р(х | θ), но неизвестно значение пара­метра θ, определяющее ее конкретно. Параметр θ может быть вектором, например, для нормального распределения θ = (μ, σ) :

В случае дискретной случайной величины р(х | θ) будет обозначать вероят­ность Р(Х - х), например для пуассоновского распределения

Пусть — некоторый числовой параметр, представлю­щий для нас интерес, например, ;; /

Рассмотрим задачу оценивания, состоящую в построе­нии такой функции t = (x₁, ...,x_n), чтобы при подстановке вме­сто аргументов х₁, ..., х_п данных выборки мы получили числа, близкие к . Такую близость можно обеспечить лишь в сред­нем. Поэтому требование, предъявляемое к качеству оценок, формулируется в вероятностных терминах, относящихся к распределению оценок, рассматриваемых как случайные величины. Это требование, состоящее в том, чтобы значения оценки в большинстве опытов были близки к значению оце­ниваемого параметра, можно сформулировать в виде следую­щего определения.

Определение. Оценка t = (x₁, ...,x_n) называется несмещенной для еслиM_θ t (x₁, ...,х_n) = для всех θ, где М_θ —символ математического ожидания при условии, что случайный вектор (x₁ ...,х_n) имеет распределение L(x| θ) = р(х₁| θ )... p(x_n| θ).

Например, как, было показано ранее, иS² — несмещенные оценки для μ и σ² соответственно.

Как правило, одно лишь требование несмещенности не выделяет оценку t(x) как лучшую. Поэтому следующим желательным требованием является обеспечение ми­нимума дисперсии этой оценки. Статистика может служить хорошей оценкой данного параметра , если ее распреде­ление сосредоточено в достаточной близости от неизвестного значения , вследствие чего вероятность больших отклоне­ний этой статистики от будет достаточно мала. Тогда присистематическом многократном применении такой статисти­ки в качестве оценки некоторой характеристики она в сред­нем окажется достаточно точной. Вероятность больших от­клонений окажется малой, т.е. они будут встречаться редко. Таким образом, среди всех несмещенных оценок t(x) для более желательной является та оценка, которая имеет мини­мальную дисперсию для всех θ. Та­кие оценки называются несмещенными оценками с мини­мальной дисперсией (НОМД).

Определение. Несмещенной оценкой с минимальной дис­персией называется такая оценка t*(x_l..., х_n), что Dt* ≤ Dt для всех

θ , для любой несмещенной оценки t(x₁ ..., х_n) параметра .

Уже эти требования, как правило, выделяют оценку t(x) однозначно, если она вообще существует. Наличие НОМД имеет место далеко не всегда, так как дисперсия для этих оце­нок должна быть минимальной равномерно по θ . Это обстоя­тельство является, пожалуй, самым серьезным аргументом против таких сильных требований.

Состоятельность оценки означает, что при достаточно большом количестве наблюдений n со сколь угодно большой достоверностью отклонение оценки от истинного значения параметра меньше любой наперед заданной величины.

Для того чтобы несмещенная оценка была состоятельной, достаточно, чтобы ее дисперсия стремилась к нулю при п→∞ (следует из неравенства Чебышева).